四元数， Physx中的四元数

 

---

 

四元数的概念 & 如何使用四元数：

 

 

 

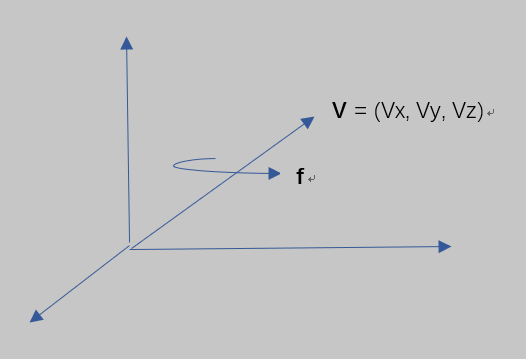
 绕V轴旋转 f 角，对应的四元数：

q = ( cos(f/2), Vx*sin(f/2), Vy*sin(f/2), Vz*sin(f/2) )

   = cos(f/2) + Vx*sin(f/2)*i + Vy*sin(f/2)*j + Vz*sin(f/2)*k

q的共轭：

q' = ( cos(f/2), -Vx*sin(f/2), -Vy*sin(f/2), -Vz*sin(f/2) )   (不应该用q'这个符号，只是为了方便打字)

 

 当前有空概念中的一个点（Wx, Wy,Wz）,求在该旋转下的新坐标W',即绕着V旋转f角， 计算方法如下：

(1)定义一个纯四元数： P = (0, Wx, Wy,Wz)

(2)运算： P'  = q*P*q', 该运算的结果P'是一个纯四元数，即第一项为0， P'的后三项即是W'的坐标哦。

 

同理，若存在一个四元数 q = (q1,q2,q3,q4) = ( cos(f/2), Vx*sin(f/2), Vy*sin(f/2), Vz*sin(f/2) )，则，其对应一个以向量(Vx,Vy,Vz)为轴 旋转f角的动作，右手法则。

 

---

四元数的乘法：

四元数有i, j, k三个虚部，i^2 = j^2 = k^2 = i*j*k = -1。

两个四元数p和q相乘的公式：

p*q = (p0,p1,p2,p3) * (q0,q1,q2,q3),     记列向量 P=(p1,p2,p3), Q = (q1,q2,q3)

      = (p0*q0 - P*Q,  p0*Q + q0*P + P x Q),   其中p0*Q + q0*P + P x Q对应一个三维向量，其三个分量为结果的i,j,k部分。

      = [ p0*q0 -  p1*q1  - p2*q2 - p3*q3 ]

         [ p0*q1 + q0*p1  + p2*q3 - p3*q2]

         [ p0*q2 + q0*p2  + p3*q1 - p1*q3]

         [ p0*q3 + q0*p3  + p1*q2 - p2*q1]

其中蓝色部分对应的是P x Q得到的向量的三个分量：

P x Q =

 

---

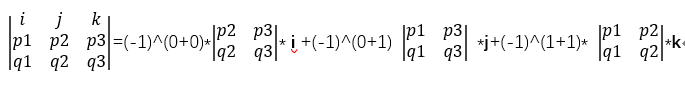
Physx引擎中的四元数

physx中的PxTransForm类：https://github.com/NVIDIAGameWorks/PhysX/blob/4.1/pxshared/include/foundation/PxTransform.h

PxQuat类 https://github.com/NVIDIAGameWorks/PhysX/blob/4.1/pxshared/include/foundation/PxQuat.h

class PxTransform

{

    PxQuat q; //四元数类，四个成员变量：（w,x,y,z）。Physx用四元数表示刚体的姿态。

    PxVec3 p; //表示刚体的位置

    PxVec3 rotate(PxVec3& input) //对输入向量做旋转,返回旋转后的向量

   {
        return q.rotate(input);
   }
   ....
};

/**
    rotates passed vec by this (assumed unitary)
    */
    PX_CUDA_CALLABLE PX_FORCE_INLINE const PxVec3 rotate(const PxVec3& v) const
    {
        const float vx = 2.0f * v.x;
        const float vy = 2.0f * v.y;
        const float vz = 2.0f * v.z;
        const float w2 = w * w - 0.5f;
        const float dot2 = (x * vx + y * vy + z * vz);
        return PxVec3((vx * w2 + (y * vz - z * vy) * w + x * dot2), (vy * w2 + (z * vx - x * vz) * w + y * dot2), (vz * w2 + (x * vy - y * vx) * w + z * dot2));
    }

    /**
    inverse rotates passed vec by this (assumed unitary)
    */
    PX_CUDA_CALLABLE PX_FORCE_INLINE const PxVec3 rotateInv(const PxVec3& v) const
    {
        const float vx = 2.0f * v.x;
        const float vy = 2.0f * v.y;
        const float vz = 2.0f * v.z;
        const float w2 = w * w - 0.5f;
        const float dot2 = (x * vx + y * vy + z * vz);
        return PxVec3( (vx * w2 - (y * vz - z * vy) * w + x * dot2), (vy * w2 - (z * vx - x * vz) * w + y * dot2),  (vz * w2 - (x * vy - y * vx) * w + z * dot2));
    }

Physx的上面代码经验证，对向量做旋转时，Physx使用的方法同《quaternions for computer graphics》中的方法一致：

存在四元数(s,x,y,z)，其中s为scalar part,用其对向量(xp,yp,zp)做一次旋转：

 

 

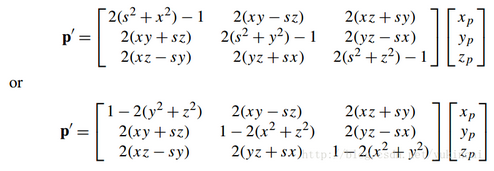
但是，跟该网页提供的matlab计算四元数旋转的方法不同::(https://ww2.mathworks.cn/help/aerotbx/ug/quatrotate.html) 该网页中的第一个简单例子的结果，套用文末的公式，得出不同的结果！

 -----------严重怀疑matlab的正确性：

用例子验证：绕Z轴(0,0,1)旋转90°的四元数为( cos(45), 0*sin(45), 0*sin(45), 1*sin(45) ) = (sqrt(2)/2, 0, 0, sqrt(2)/2);

用该四元数旋转(1,0,0):

----使用Physx中的方法结果为（0,1,0）

----使用matlab的计算结果为(0,-1,0)， 是沿着反方向转了90°。----- （在physx的方法中，输入的四元数对应的是旋转角度的一般，难道matlab中输入的四元数意义不同吗，默认是左手法则吗，这导致上面的公式中 与书本上的公式有正负号差异吗？待探索）

 

---

 

Physx中的四元数类的使用总结哦：

 

有全局坐标系A和局部坐标系A’,  A经过一定的动作后与A’的姿态重合，（例如，A绕自己的Z(0,0,1)轴旋转90度），该动作可以用一个四元数表示出来（eg. quat(x,y,z ,w) =  (0, 0, 1*sin(90/2), cos(90/2)), w为scalar part ）。

 

1） 局部系转到全局系：

存在一个空间向量b,该向量在A’中的表示为b_local=（1,0,0）, 则该向量在A中的表示为：

将全局系下的(1,0,0)绕z轴旋转90度（画图便理解）: quat.rotate(b_local)。

 

2）全局系转到局部系：

存在一个空间向量c,该向量在A中的表示为c_local=（1,0,0）, 则该向量在A’中的表示为：

方法1：将全局系下的(1,0,0)绕z轴旋转-90度:

quat_new(x,y,z ,w) =  (0, 0, 1*sin(-90/2), cos(-90/2))

quat_new.rotate(c_local)。

 

方法2：quat. rotateInv(c_local)

 

3）

 -----可以得到对应的旋转矩阵啦！

 

 

Physx中的PxTransform类的使用总结

 

https://www.cnblogs.com/butterflybay/p/13276763.html

 

 

 

---

 

四元数与欧拉角 

关于欧拉角很好文章： https://www.cnblogs.com/21207-iHome/p/6894128.html  

 

四元数转换为欧拉角： （Physx中的四元数类并没有提供这个功能）

1. 开源opengl库https://github.com/g-truc/glm 或许有

2. Unreal Engine中的方法

https://docs.unrealengine.com/4.26/en-US/API/Runtime/Core/Math/FRotator/
https://docs.unrealengine.com/4.27/en-US/API/Runtime/Core/Math/FQuat/

float ClampAxis(float Angle) // degree
  {
    // returns Angle in the range (-360,360)
    Angle = std::fmod(Angle, 360.f);

    if (Angle < 0.f)
    {
      // shift to [0,360) range
      Angle += 360.f;
    }

    return Angle;
  }

  float NormalizeAxis(float Angle) // degree
  {
    // returns Angle in the range [0,360)
    Angle = ClampAxis(Angle);

    if (Angle > 180.f)
    {
      // shift to (-180,180]
      Angle -= 360.f;
    }

    return Angle;
  }

  // Refer to FRotator::FRotator(const FQuat& Quat);
  std::vector<float> QUat2Euler(const float X, const float Y, const float Z, const float W)
  {
    //
    const float SingularityTest = Z * X - W * Y;
    const float YawY = 2.f * (W * Z + X * Y);
    const float YawX = (1.f - 2.f * (Y*Y + Z*Z));

    // reference
    // http://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
    // http://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/

    // this value was found from experience, the above websites recommend different values
    // but that isn't the case for us, so I went through different testing, and finally found the case
    // where both of world lives happily.
    const float SINGULARITY_THRESHOLD = 0.4999995f;
    const float PI = 3.1415926535897932f;
    const float RAD_TO_DEG = (180.f) / PI;
    const float DEG_TO_RAD = PI /(180.f);

    float Pitch = 0.0f;
    float Yaw = 0.0f;
    float Roll = 0.0f;

    if (SingularityTest < -SINGULARITY_THRESHOLD)
    {
      Pitch = -90.f;
      Yaw = std::atan2(YawY, YawX) * RAD_TO_DEG;
      Roll = NormalizeAxis(-Yaw - (2.f * std::atan2(X, W) * RAD_TO_DEG));
    }
    else if (SingularityTest > SINGULARITY_THRESHOLD)
    {
      Pitch = 90.f;
      Yaw = std::atan2(YawY, YawX) * RAD_TO_DEG;
      Roll = NormalizeAxis(Yaw - (2.f * std::atan2(X, W) * RAD_TO_DEG));
    }
    else
    {
      Pitch = std::asin(2.f * (SingularityTest)) * RAD_TO_DEG;
      Yaw = std::atan2(YawY, YawX) * RAD_TO_DEG;
      Roll = std::atan2(-2.f * (W * X + Y * Z), (1.f - 2.f * (X*X + Y*Y))) * RAD_TO_DEG;
    }
    std::cout << "Roll, Pitch, Yaw: " << Roll << " " << Pitch << " " <<  Yaw << std::endl;
    return std::vector<float>{Roll, Pitch, Yaw}; // degree
  }

 

3. wiki 现成函数

  https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles#Quaternion_to_Euler_angles_conversion

struct Quaternion {
    double w, x, y, z;
};

struct EulerAngles {
    double roll, pitch, yaw;
};

EulerAngles ToEulerAngles(Quaternion q) {
    EulerAngles angles;

    // roll (x-axis rotation)
    double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
    double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
    angles.roll = std::atan2(sinr_cosp, cosr_cosp);

    // pitch (y-axis rotation)
    double sinp = 2 * (q.w * q.y - q.z * q.x);
    if (std::abs(sinp) >= 1)
        angles.pitch = std::copysign(M_PI / 2, sinp); // use 90 degrees if out of range
    else
        angles.pitch = std::asin(sinp);

    // yaw (z-axis rotation)
    double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
    double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
    angles.yaw = std::atan2(siny_cosp, cosy_cosp);

    return angles;
}

 

 

其他：

 

 

 

---

 

Matlab: 四元数与欧拉角转换

https://www.mathworks.com/help/fusion/ref/quaternion.eulerd.html

 

---

 

四元数连乘的意义

以下自自己想的，还没看其他资料的解释，应该是对的吧：

 

 

 

 

---

 

“现在主流游戏或动画引擎都会以 缩放向量+旋转四元数+平移向量的形式进行存储角色的运动数据。”

 

https://www.zhihu.com/question/23005815/answer/33971127、

https://www.qiujiawei.com/understanding-quaternions/?utm_source=wechat_session&utm_medium=social&utm_oi=984341909149577216

https://zhuanlan.zhihu.com/p/27471300

https://www.zhihu.com/topic/19594299/top-answers

 

经典书： 《quaternions for computer graphics 》https://max.book118.com/html/2018/0220/153945618.shtm

 

===2019.10.26 将physx中的class PxTransform类的四元数旋转函数终于搞清楚了：

查阅的链接：

https://docs.nvidia.com/gameworks/content/gameworkslibrary/physx/apireference/files/

https://docs.nvidia.com/gameworks/content/gameworkslibrary/physx/apireference/files/hierarchy.html

http://www.doc88.com/p-805243984870.html

https://ww2.mathworks.cn/help/robotics/ref/eul2quat.html

https://ww2.mathworks.cn/help/robotics/ref/quaternion.rotmat.html

https://ww2.mathworks.cn/help/robotics/ref/quaternion.mtimes.html

https://ww2.mathworks.cn/help/robotics/ref/quaternion.html

---

 

该文章相当好：

http://www.geeks3d.com/20141201/how-to-rotate-a-vertex-by-a-quaternion-in-glsl/

摘录在此：

In a vertex shader, the rotation and position are usually encoded in the model matrix and we have something like this:

vec4 worldPos = ModelMatrix * InPosition;    -- 旋转矩阵的形式

Here is another method to transform the position of a vertex, using a quaternion to hold the rotation information. Quaternions are a fantastic mathematics tool discovered by Sir William Rowan Hamilton in 1843. We’re not going to review quaternions in detail here, because I’m not a mathematician and it’s not the point. We’re going to see how to use them in practice in a GLSL program to rotate a vertex.

A quaternion can be seen as a object that holds a rotation around any axis. A quaternion is a 4D object defined as follows:

q = [s, v] 
q = [s + xi + yj + zk]

where s, x, y and z are real numbers. s is called the scalar part while x, y and z form the vector part.   i, j and k are imaginary numbers. Quaternions are the generalization of complex numbers in higher dimensions.

In 3D programming, we store quaternions in a 4D vector:

q = [x, y, z, w]   -- x,y,z对应向量部分。

where w = s and [x, y, z] = v.

Now let’s see the fundamental relation that makes it possible to rotate a point P0 around an rotation axis encoded in the quaternion q:

P1 = q P0 q-1

where P1 is the rotated point and q^-1 is the inverse of the quaternion q (q的共轭).

From this relation we need to know:
1 – how to transform a rotation axis into a quaternion.
2 – how to transform a position into a quaternion.
3 – how to get the inverse of a quaternion.
4 – how to multiply two quaternions.

Remark: all the following rules expect an unit quaternion. An unit quaternion is a quaternion with a norm of 1.0. A quaternion can be normalized with:

norm = sqrt(q.x*q.x + q.y*q.y + q.z*q.z + q.w*q.w)
q.x =  q.x / norm
q.y =  q.y / norm
q.z =  q.z / norm
q.w =  q.w / norm

1 – How to transform a rotation axis into a quaternion

Here is a formula that converts a rotation around an axis (defined by the couple [axis, angle]) into a quaternion:

绕向量(axis.x, axis.y, axis.z)旋转angle对应的四元数：

half_angle = angle/2
q.x = axis.x * sin(half_angle)
q.y = axis.y * sin(half_angle)
q.z = axis.z * sin(half_angle)
q.w = cos(half_angle)

2 – How to transform a position into a quaternion

The position is usually a 3D vector: {x, y, z}. This position can be represented in a quaternion by setting to zero the scalar part and initializing the vector part with the xyz-position:

q.x = position.x
q.y = position.y
q.z = position.z
q.w = 0

The quaternion q=[x, y, z, 0] is a pure quaternion because it has not real part.

------- 这部分的作用应该是：要对向量{x, y, z}基于四元数做旋转时，需要先将该向量转换为一个纯四元数。

3 – How to get the inverse of a quaternion

The inverse of a quaternion is defined by the following relation:

q = [x, y, z, w]
norm = |q| = sqrt(q.x*q.x + q.y*q.y + q.z*q.z + q.w*q.w)
q

^-1

 = [-x, -y, -z, w] / |q|        -------------------------------------------即，将旋转角取反。
q

^-1

= [-x/|q|, -y/|q|, -z/|q|, w/|q|]

If we have an unit quaternion, |q|=1 and the inverse is equal to the conjugate (q^*) of the quaternion:  ---- 看来四元数q的逆等于其共轭除以其模长。

q

^-1

= q

^*

= [-x, -y, -z, w]

4 – How to multiply two quaternions

Quaternions can be multiplied:

q = q1 * q2

But like for matrix multiplication, quaternion multiplication is non-commutative:

(q1 * q2) != (q2 * q1)

The multiplication of two quaternions is defined by:

q.x = (q1.w * q2.x) + (q1.x * q2.w) + (q1.y * q2.z) - (q1.z * q2.y)
q.y = (q1.w * q2.y) - (q1.x * q2.z) + (q1.y * q2.w) + (q1.z * q2.x)
q.z = (q1.w * q2.z) + (q1.x * q2.y) - (q1.y * q2.x) + (q1.z * q2.w)
q.w = (q1.w * q2.w) - (q1.x * q2.x) - (q1.y * q2.y) - (q1.z * q2.z)

Now we have all tools to rotate a point around an axis in a GLSL vertex shader:

#version 150
in vec4 gxl3d_Position;
in vec4 gxl3d_TexCoord0;
in vec4 gxl3d_Color;
out vec4 Vertex_UV;
out vec4 Vertex_Color;
uniform mat4 gxl3d_ViewProjectionMatrix;

struct Transform
{
  vec4 position;
  vec4 axis_angle;
};
uniform Transform T;


vec4 quat_from_axis_angle(vec3 axis, float angle) -- 给定一个向量，以及绕该向量旋转的角，求其对用的四元数
{ 
  vec4 qr;
  float half_angle = (angle * 0.5) * 3.14159 / 180.0;
  qr.x = axis.x * sin(half_angle);
  qr.y = axis.y * sin(half_angle);
  qr.z = axis.z * sin(half_angle);
  qr.w = cos(half_angle);
  return qr;
}

vec4 quat_conj(vec4 q)------------------------------给定一个四元数，求其共轭
{ 
  return vec4(-q.x, -q.y, -q.z, q.w); 
}
  
vec4 quat_mult(vec4 q1, vec4 q2)---------------------给定两个四元数，求其乘积
{ 
  vec4 qr;
  qr.x = (q1.w * q2.x) + (q1.x * q2.w) + (q1.y * q2.z) - (q1.z * q2.y);
  qr.y = (q1.w * q2.y) - (q1.x * q2.z) + (q1.y * q2.w) + (q1.z * q2.x);
  qr.z = (q1.w * q2.z) + (q1.x * q2.y) - (q1.y * q2.x) + (q1.z * q2.w);
  qr.w = (q1.w * q2.w) - (q1.x * q2.x) - (q1.y * q2.y) - (q1.z * q2.z);
  return qr;
}

vec3 rotate_vertex_position(vec3 position, vec3 axis, float angle)----给定一个轴以及绕该轴旋转的角，以及一个空间向量，求该向量绕该轴旋转后的向量
{ 
  vec4 qr = quat_from_axis_angle(axis, angle);
  vec4 qr_conj = quat_conj(qr);
  vec4 q_pos = vec4(position.x, position.y, position.z, 0);
  
  vec4 q_tmp = quat_mult(qr, q_pos);
  qr = quat_mult(q_tmp, qr_conj);
  
  return vec3(qr.x, qr.y, qr.z);
}

void main()
{
  vec3 P = rotate_vertex_position(gxl3d_Position.xyz, T.axis_angle.xyz, T.axis_angle.w);
  P += T.position.xyz;
  gl_Position = gxl3d_ViewProjectionMatrix * vec4(P, 1);
  Vertex_UV = gxl3d_TexCoord0;
  Vertex_Color = gxl3d_Color;
}

This powerful vertex shader comes from the host_api/RubikCube/Cube_Rotation_Quaternion/demo_v3.xml demo you can find in the code sample pack. To play with this demo, GLSL Hacker v0.8+ is required.

 

 

Some references:

• Quaternions
• Quaternions and spatial rotation
• Understanding Quaternions
• Quaternions – transforming spatials – Kri, modern OpenGL 3 engine
• Book: Mathematics for Computer Graphics by John Vince

 

 

---