推荐系统中的协同滤波算法___使用SVD

 

对于推荐方法，基于内容 和 基于协同过滤 是目前的主流推荐算法，很多电子商务网站的推荐系统都是基于这两种算法的。

协同过滤 是一种基于相似性来进行推荐的算法，主要分为 基于用户的协同过滤算法 和 基于项目的协同过滤算法，第3种是基于模型(model based)的协同过滤。

协同：通过在线数据找到用户可能喜欢的物品；      过滤：滤掉一些不值得推荐的数据

 

基于用户的(User based)协同过滤算法:

采用统计计算方式，搜索目标用户的相似用户（通过相似性度量方法计算出最近邻居集合），并根据相似用户对项目的打分来预测目标用户对某些项目的评分，然后找出预测最高的若干个物品推荐给用户。

基于项目的(Item一based)协同过滤算法：

基于项目(item-based)的协同过滤和基于用户的协同过滤类似，只不过这时我们转向物品和物品之间的相似度。如果目标用户对某些物品已经评分，我们就可以找出与这些物品相似度高的物品并预测目标用户对它们的评分，将评分最高的若干个相似物品推荐给用户。比如你在网上买了一本机器学习相关的书，网站马上会推荐一堆机器学习相关的书给你，这里就明显用到了基于项目的协同过滤思想。

 

基于用户的协同过滤可以帮助用户找到新类别的有惊喜的物品。而基于项目的协同过滤，由于物品的相似性一段时间不会变，很难带给用户惊喜了。一般对于小型的推荐系统来说，基于项目的协同过滤肯定是主流。
 

---

举例理解协同滤波 以及 SVD在协同滤波中的使用：

首先，关于奇异值分解(SVD)的数学理论，这里暂且不讲。

假设我们有一个矩阵，该矩阵每一列代表一个user，每一行代表一个item，例如这些item可以是电影。

矩阵值代表user对item的评分，0代表未评分。

SVD是将一个大的矩阵进行有损地压缩。用一个具体的例子展示svd：

首先是A矩阵，对应上面的评分矩阵：

A =

     5     5     0     5
     5     0     3     4
     3     4     0     3
     0     0     5     3
     5     4     4     5
     5     4     5     5

使用matlab调用svd函数：

[U,S,Vtranspose]=svd(A)

U =
   -0.4472   -0.5373   -0.0064   -0.5037   -0.3857   -0.3298
   -0.3586    0.2461    0.8622   -0.1458    0.0780    0.2002
   -0.2925   -0.4033   -0.2275   -0.1038    0.4360    0.7065
   -0.2078    0.6700   -0.3951   -0.5888    0.0260    0.0667
   -0.5099    0.0597   -0.1097    0.2869    0.5946   -0.5371
   -0.5316    0.1887   -0.1914    0.5341   -0.5485    0.2429

S =
   17.7139         0         0         0
         0    6.3917         0         0
         0         0    3.0980         0
         0         0         0    1.3290
         0         0         0         0
         0         0         0         0

Vtranspose =
   -0.5710   -0.2228    0.6749    0.4109
   -0.4275   -0.5172   -0.6929    0.2637
   -0.3846    0.8246   -0.2532    0.3286
   -0.5859    0.0532    0.0140   -0.8085

SVD将矩阵A分解成三个矩阵的乘积：A = U * S * (Vtranspose)'，这里我用(x)‘表示x的转置。其中S是一个对角线矩阵，对角线上的元素非负，是A的奇异值，从上到下逐渐减小。

为了对矩阵A进行降维压缩，取S对角线上前k个元素。当k=2时候，将S(6*4)降维成S(2*2)，同时U(6*6)变为 U(6*2), (Vtranspose)'(4*4)变为 (Vtranspose)'(2*4).

如下图：

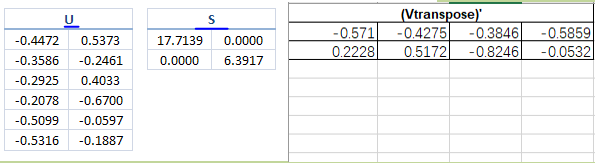
此时我们用降维后的U，S，(Vtranspose)'来相乘得到A2

A2 =

    5.2885    5.1627    0.2149    4.4591
    3.2768    1.9021    3.7400    3.8058
    3.5324    3.5479   -0.1332    2.8984
    1.1475   -0.6417    4.9472    2.3846
    5.0727    3.6640    3.7887    5.3130
    5.1086    3.4019    4.6166    5.5822

此时我们可以很直观地看出，A2和A很接近----有损压缩。

既然两者很接近，那么我们就可以利用压缩后的数据来进行相似性分析啦：

将降维后的U的第一列当成x值，第二列当成y值,即U的每一行作为一个数据点画在图中；

类似地，将降维后(Vtranspose)'的每一列作为一个数据点画在图中：

之所以这样，是因为降维后U中的各个行之间的相似性 可以近似代表 原始矩阵A中各个行(each user)之间的相似性；

降维后(Vtranspose)'中的各个列之间的相似性 可以近似代表 原始矩阵A中各个列(each item)之间的相似性；

从纯数学上可以这样理解：

A = USV  --->  (US) * V = A，所以A中的第i列 是由V中的第i列变换而来的！

A = USV  --->  U * (SV) = A，所以A中的第i行 是由U中的第i行变换而来的！

从图中可以看出: Season5，Season6特别靠近， 用户Ben和Fred特别靠近。

观察A矩阵可以看出，A矩阵的第5行向量和第6行向量特别相似，Ben所在列向量和Fred所在列向量也特别相似。从直观上我们发现U矩阵和V矩阵可以近似来代表A矩阵，换据话说就是将A矩阵压缩成U矩阵和V矩阵。

 

至此，数据压缩的部分已经完成，接下来需要解决实际问题：

以寻找相似用户为例子(基于user的推荐)：

假设，现在我们突然得到了名字叫Bob的新用户，且已知Bob对6个item评分向量为：[5 5 0 0 0 5]（列向量）。任务是要给做出个性化的推荐，即向他推荐他可能喜欢的item。

首先, 利用Bob的评分向量找出其相似用户。现在，我们在使用svd, 我们已经将之前得到的其他的用户进行了降维，前面已经提到原始矩阵A中的各列与降维后(Vtranspose)'的各列相似，相当于我们对原始的各个列(用户)施加了一个降维动作，将其由6*1压缩为了2*1。

现在，我们得到了新用户Bob的数据，相当于一个6*1的列，需要对其也施加一个相同的降维动作，将其压缩压缩为2*1,然后将这个得到的2*1向量与其他的进行快速比较，这个降维动作是什么呢？ 

如上图（图中第二行式子有错误，Bob的转置应为行向量）。

对图中公式不做证明，只需要知道结论，结论是得到一个Bob的二维向量，即知道Bob的坐标。

将Bob坐标添加进原来的图中：

然后从图中找出和Bob最相似的用户。

注意，最相似并不是距离最近的用户，这里的相似用余弦相似度计算。（关于相似度还有很多种计算方法，各有优缺点）

即夹角与Bob最小的用户坐标。

可以计算出最相似的用户是ben。

接下来的推荐策略就完全取决于个人选择了。

 

Ref:

https://blog.csdn.net/hhtnan/article/details/79854525

---

https://yanyiwu.com/work/2012/09/10/SVD-application-in-recsys.html

上面这一篇有一个地方没有讲明白：对新用户进行评分预测时，为什么要做文章中提到的处理方式？《机器学习实战》中也是使用了相同的方法。SVD的意义应该是将高维映射到低维空间，从而可以在低维空间中更快地进行相似度的比较。例如，如果要比较两个item的相似度，假设原始矩阵A维度为1000*8，有1000个用户，8部电影。假设用户1没有对第1步电影进行评分，现在需要对该项进行用基于item的协同滤波算法进行预测，从而需要将第1部电影与其他电影进行比较，即将矩阵的第1列与其他各列进行比较，但是各列都是1000维的向量，比较起来比较耗时，另外有很多稀疏。这时，SVD便可以起到作用，可以将列映射到低维空间。映射的方法就是先将原始矩阵A进行奇异值分解，A=U*diag*V，然后仅仅保留diag对角阵中的前10（假设）个元素即可保存A的90%的信息，A≈U2*diag_2*V2，矩阵V2中的各个列可以近似反应原始矩阵中各个列的相似关系（原因？还没理解），从而比较A中的各个列的相似度可以转换为比较V2中个列的相似度，而V2中各个列都是10维的向量。

将矩阵A中各个列转换为V2中各个列的过程：即将V2用A表示出来，根据A(1000,8)=U(1000,1000)*diag(1000,8)*V(8,8)且U，V都为正交矩阵(自身的转置等于逆)，可知 V=inv(diag)trans(U)*A, 保留对角阵的前r个元素：

V2(r,8) ≈ inv(diag2(r,r)) * trans(U2(1000,r)) * A(1000,8)。

另，如果有新的电影（不在原始A中）需要被估计分数，同样地，可以将该电影对应的列向量转换到低维空间，再与其他已经被转换的电影列向量进行比较。可以将V2(r,8) ≈ inv(diag2(r,r)) * trans(U2(1000,r)) * A(1000,8) 理解为

[v1，v, ...,v8] ≈ G*[a1,a2,...., a8]，vi和ai都是列向量，vi≈G*ai,转换关系，据G可以由新来的列向量求出低维的vi。

 

至于，A≈U2*diag_2*V2，矩阵V2中的各个列可以近似反应原始矩阵中各个列的相似关系的原因：

可以结合PCA 与SVD之间的关系来理解。对于PCA来说：

假设有m个样本x(1),x(2),...,x(m),都是列向量，每个样本都是n维，即含有n个features，记X=[x(1),x(2),...,x(m)], 如果要从n维降到r维，根据推导过程可知，首先需要求出X*trans(X)的前r个最大的特征值对应的特征向量：u1,u2,..,ur， 这些特征向量即为主方向，然后将各个x(i)向主方向投影，x(i)被转换为r维的列向量，各个元素为：x(i)*trans(u1), x(i)*trans(u2), ..., x(i)*trans(ur)。用矩阵可以表示为：

记作：

G*X=P

可以单纯从矩阵的角度来分析，G矩阵的第i行向X各列对应的u1,u2,...,ur向量方向投影得到P矩阵的第i行，G矩阵中的各行的关系近似于P矩阵中各行的关系。

对于奇异值分解来说，A(m,n) = U(m,m) * diag(m,n) * V(n,n)

===》A*（inv(V)*inv(diag)） = U，类比PCA可知，A和U的行向量是相似的，此公式将A中行向量压缩成U中的低维行

向量（是用SVD来代替PCA的一种方法）。

===》inv(diag)*inv(U)*A = V，即inv(diag)*inv(U)*[a1,a2,...,an] = [v1,v2,...,vn],A和V的列向量是相似的，比较A中的各个列之间的相似度就可以相当于比较V中各个列之间的相似度。此公式将A列向量压缩成V中的低维列向量。

 

所以，可以利用奇异值分解，方便地对原始矩阵进行行向量或列向量的压缩。

 

 

其他：

http://blog.csdn.net/u012448083/article/details/54959447

基于SVD的优势在于：用户的评分数据是稀疏矩阵，可以用SVD将原始数据映射到低维空间中，然后计算物品item之间的相似度，可以节省计算资源。

 

Author：frank

参考：机器学习实战

http://blog.sina.com.cn/s/blog_73de143c010153vp.html