进阶:2.GBDT算法梳理
GBDT算法梳理
学习内容:
1.前向分布算法
2.负梯度拟合
3.损失函数
4.回归
5.二分类,多分类
6.正则化
7.优缺点
8.sklearn参数
9.应用场景
1.前向分布算法
在学习模型时,每一步只学习一个基函数及其系数,逐步逼近优化函数式,从而简化优化的复杂度。

2.负梯度拟合
针对这个问题,大牛Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值,进而拟合一个CART回归树。第t轮的第i个样本的损失函数的负梯度表示为
$r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partial f(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} $
利用(xi,rti)(i=1,2,..m)(xi,rti)(i=1,2,..m),我们可以拟合一颗CART回归树,得到了第t颗回归树,其对应的叶节点区域Rtj,j=1,2,...,JRtj,j=1,2,...,J。其中J为叶子节点的个数。
针对每一个叶子节点里的样本,我们求出使损失函数最小,也就是拟合叶子节点最好的的输出值ctjctj如下:
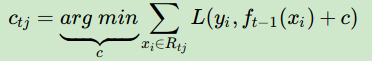
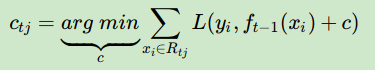
从而本轮最终得到的强学习器的表达式如下:
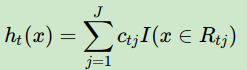
通过损失函数的负梯度来拟合,我们找到了一种通用的拟合损失误差的办法,这样无轮是分类问题还是回归问题,我们通过其损失函数的负梯度的拟合,就可以用GBDT来解决我们的分类回归问题。区别仅仅在于损失函数不同导致的负梯度不同而已。
3.损失函数
对于分类算法,其损失函数一般有对数损失函数和指数损失函数两种:
a) 如果是指数损失函数,则损失函数表达式为
$L(y, f(x)) = exp(-yf(x))$
b) 如果是对数损失函数,分为二元分类和多元分类两种.
对于回归算法,常用损失函数有如下4种:
a)均方差,这个是最常见的回归损失函数了
$L(y, f(x)) =(y-f(x))^2$
b)绝对损失,这个损失函数也很常见
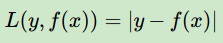
对应负梯度误差为:
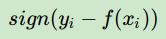
c)Huber损失,它是均方差和绝对损失的折衷产物,对于远离中心的异常点,采用绝对损失,而中心附近的点采用均方差。这个界限一般用分位数点度量。损失函数如下:
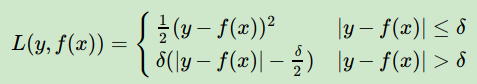
对应的负梯度误差为:
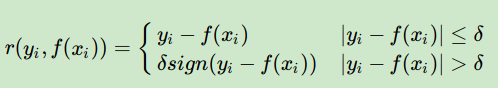
d) 分位数损失。它对应的是分位数回归的损失函数,表达式为
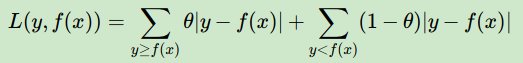
其中θ为分位数,需要我们在回归前指定。对应的负梯度误差为:
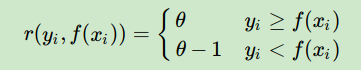
对于Huber损失和分位数损失,主要用于健壮回归,也就是减少异常点对损失函数的影响。
4.回归
输入是训练集样本$T=\{(x_,y_1),(x_2,y_2), ...(x_m,y_m)\}$, 最大迭代次数T, 损失函数L。
输出是强学习器f(x)输出是强学习器f(x)
1) 初始化弱学习器$f_0(x) = \underbrace{arg\; min}_{c}\sum\limits_{i=1}^{m}L(y_i, c) $
2) 对迭代轮数t=1,2,...T有:
a)对样本i=1,2,...m,计算负梯度
$r_{ti} = -\bigg[\frac{\partial L(y_i, f(x_i)))}{\partialf(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} $
b)利用$(x_i,r_{ti})\;\; (i=1,2,..m)$, 拟合一颗CART回归树,得到第t颗回归树,其对应的叶子节点区域为$R_{tj}, j =1,2,..., J$。其中J为回归树t的叶子节点的个数。
c) 对叶子区域j =1,2,..J,计算最佳拟合值
$c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} L(y_i,f_{t-1}(x_i) +c) $
d) 更新强学习器
$f_{t}(x) = f_{t-1}(x) + \sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) $
3) 得到强学习器f(x)的表达式$f(x) = f_T(x) =f_0(x) + \sum\limits_{t=1}^{T}\sum\limits_{j=1}^{J}c_{tj}I(x \in R_{tj}) $
5.二分类,多分类
二分类
对于二元GBDT,如果用类似于逻辑回归的对数似然损失函数,则损失函数为:$L(y, f(x)) = log(1+ exp(-yf(x))) $
其中$y \in\{-1, +1\}$。则此时的负梯度误差为
$r_{ti} = -\bigg[\frac{\partial L(y, f(x_i)))}{\partialf(x_i)}\bigg]_{f(x) = f_{t-1}\;\; (x)} = y_i/(1+exp(y_if(x_i))) $
对于生成的决策树,我们各个叶子节点的最佳负梯度拟合值为
$c_{tj} = \underbrace{arg\; min}_{c}\sum\limits_{x_i \in R_{tj}} log(1+exp(-y_i(f_{t-1}(x_i) +c))) $
由于上式比较难优化,我们一般使用近似值代替
$c_{tj} =sum\limits_{x_i \in R_{tj}}r_{ti}\bigg /\sum\limits_{x_i \in R_{tj}}|r_{ti}|(1-|r_{ti}|) $
除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索,二元GBDT分类和GBDT回归算法过程相同。
多分类
多元GBDT要比二元GBDT复杂一些,对应的是多元逻辑回归和二元逻辑回归的复杂度差别。假设类别数为K,则此时我们的对数似然损失函数为:
$L(y, f(x)) = - \sum\limits_{k=1}^{K}y_klog\;p_k(x) $
其中如果样本输出类别为k,则$y_k=1$。第k类的概率$p_k(x)$的表达式为:
$p_k(x) = exp(f_k(x)) \bigg / \sum\limits_{l=1}^{K}exp(f_l(x)) $
集合上两式,我们可以计算出第$t$轮的第$i$个样本对应类别$l$的负梯度误差为
$r_{til} =-\bigg[\frac{\partial L(y_i, f(x_i)))}{\partialf(x_i)}\bigg]_{f_k(x) = f_{l, t-1}\;\; (x)} = y_{il} - p_{l, t-1}(x_i) $
观察上式可以看出,其实这里的误差就是样本$i$对应类别$l$的真实概率和$t-1$轮预测概率的差值。
对于生成的决策树,我们各个叶子节点的最佳负梯度拟合值为
$c_{tjl} = \underbrace{arg\; min}_{c_{jl}}\sum\limits_{i=0}^{m}\sum\limits_{k=1}^{K}L(y_k, f_{t-1, l}(x) + \sum\limits_{j=0}^{J}c_{jl} I(x_i \in R_{tj})) $
由于上式比较难优化,我们一般使用近似值代替
$c_{tjl} = \frac{K-1}{K} \; \frac{\sum\limits_{x_i \in R_{tjl}}r_{til}}{\sum\limits_{x_i \in R_{til}}|r_{til}|(1-|r_{til}|)} $
除了负梯度计算和叶子节点的最佳负梯度拟合的线性搜索,多元GBDT分类和二元GBDT分类以及GBDT回归算法过程相同
6.正则化
GBDT的正则化主要有三种方式:
第一种是和Adaboost类似的正则化项,即步长(learning rate)。定义为$\nu$,对于前面的弱学习器的迭代$f_{k}(x) = f_{k-1}(x) + h_k(x) $
如果我们加上了正则化项,则有$f_{k}(x) = f_{k-1}(x) + \nu h_k(x) $
$\nu$的取值范围为$0 - 1 $。对于同样的训练集学习效果,较小的$\nu$意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。
第二种正则化的方式是通过子采样比例(subsample)。取值为(0,1]。注意这里的子采样和随机森林不一样,随机森林使用的是放回抽样,而这里是不放回抽样。如果取值为1,则全部样本都使用,等于没有使用子采样。如果取值小于1,则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差,即防止过拟合,但是会增加样本拟合的偏差,因此取值不能太低。推荐在[0.5, 0.8]之间。
使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。由于使用了子采样,程序可以通过采样分发到不同的任务去做boosting的迭代过程,最后形成新树,从而减少弱学习器难以并行学习的弱点。
第三种是对于弱学习器即CART回归树进行正则化剪枝。
7.优缺点
GBDT主要的优点有:
1) 可以灵活处理各种类型的数据,包括连续值和离散值。
2) 在相对少的调参时间情况下,预测的准确率也可以比较高。这个是相对SVM来说的。
3)使用一些健壮的损失函数,对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。
GBDT的主要缺点有:
由于弱学习器之间存在依赖关系,难以并行训练数据。不过可以通过自采样的SGBT来达到部分并行。
8.sklearn参数
class sklearn.ensemble.GradientBoostingClassifier(
loss=’deviance’, 可选: {‘deviance’, ‘exponential’}, optional (default=’deviance’),优化的损失函数
learning_rate=0.1, float, optional (default=0.1),学习率
n_estimators=100, int (default=100),boosting的数量
subsample=1.0, float, optional (default=1.0),下采样的比率
criterion=’friedman_mse’, string, optional (default=”friedman_mse”),衡量分类质量的标准
min_samples_split=2, int, float, optional (default=2),分支的最少量
min_samples_leaf=1, int, float, optional (default=1),每个分支样本的最少量
min_weight_fraction_leaf=0.0, float, optional (default=0.),最小分支权重
max_depth=3, integer, optional (default=3),树的最大深度
min_impurity_decrease=0.0, float, optional (default=0.),如果该分裂导致杂质的减少大于或等于该值,则将分裂节点。
min_impurity_split=None, float, (default=1e-7),树停止分裂的条件
init=None, estimator, optional,初始化模型方法,fit or predict
random_state=None, int, RandomState instance or None, optional (default=None),打乱样本时选用的随机种子
max_features=None, int, float, string or None, optional (default=None),在寻找最佳分支时,考虑的
verbose=0, int, default: 0,启用详细输出
max_leaf_nodes=None, int or None, optional (default=None),最大叶子节点
warm_start=False,bool, default: False,是否使用已有的模型进行优化
presort=’auto’, bool or ‘auto’, optional (default=’auto’),是否对数据进行排序以加快数据的寻找速度
validation_fraction=0.1, float, optional, default 0.1,验证集的比率
n_iter_no_change=None, int, default None,当验证集分数不在提高时,是否提前停止
tol=0.0001,float, optional, default 1e-4,提前停止优化的标准
9.应用场景


 浙公网安备 33010602011771号
浙公网安备 33010602011771号