线段树

线段树

线段树的基本结构

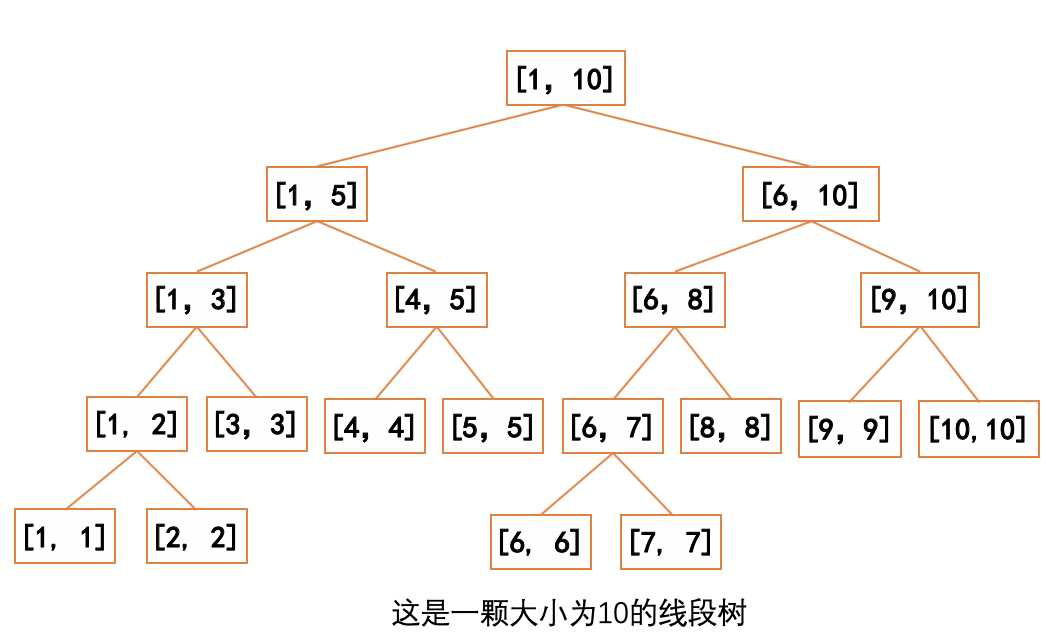
• 线段树将每个长度不为 \(1\) 的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两区间信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。

• 我们可以按照满二叉树的形式从上到下从左到右依次给线段树上的节点编号

  那么对于节点 \(d_i\) ，其左儿子为 \(d_{2i}\)，右儿子为 \(d_{2i+1}\)

• 每向下一层，对应的区间长度减半

建树

• 为了方便，写几个宏定义

  #define ls (k << 1);，左孩子

  #define rs (k << 1 | 1);，右孩子

  #define mid ((l + r) >> 1);，中间点

• 令 \(S(k)\) 为 \(k\) 对应区间的区间和（这里的 \(k\) 是节点编号）

  则 \(S(k)=S(ls)+S(rs)\)，当 \(l=r\) 时到达叶子节点停止递归

• void build(int k,int l,int r){
      if(l == r){
          S[k] = A[l];
          return;
      }
      build(ls,l,mid);
      build(rs,mid+1,r);
      S[k] = S[ls]+S[rs];
      return;
  }
  

单点修改

• void pushup(int k,int l,int r){
      S[k] = S[ls] + S[rs];
  }
  
  void plus(int k,int l,int r,int x,int v){
      if(l == r){
          S[l] += v;
          return;
      }
      if(x <= mid) plus(ls,l,mid,k,v);
      else plus(rs,mid+1,r,k,v);
      pushup(k,l,r);
  }
  

• pushup函数负责向上更新祖先的信息

• 在plus函数中，通过判断 \(x\) 与区间中点的关系来更新包含 \(x\) 的区间

区间求和

• 考虑当前节点 \(k\) 所对应的区间 \([l,r]\) 与 \([x,y]\) 的关系

  若 \([x,y]\) 包含 \([l,r]\)，则将 \(S(k)\) 全部计入答案

  否则若 \([x,y]\) 包含 \([l,mid]\) ，递归 \(ls\)

  若 \([x,y]\) 包含 \([mid+1,r]\)，递归 \(rs\)

• int ask(int k,int l,int r,int x,int y){
      if(x <= l && r <= y) return S[k];
      int res = 0;
      if(x <= mid) res += ask(ls,l,  mid,x,y);
      if(y >  mid) res += ans(rs,mid+1,r,x,y);
      return res;
  }
  

区间修改

• 如果要求修改区间 \([l,r]\) ，把所有包含在区间 \([l,r]\) 中的节点都遍历一次、修改一次，时间复杂度无法承受。我们这里要引入一个叫做 「懒惰标记」 的东西。

• 懒标记：\(\text{lazy}(k)\)代表将k对应的区间整体加 \(k\)

  当我们需要对点 \(k\) 所对应的区间加 \(v\) 时，我们不递归 \(k\) 的左右子树更新其内部值，而是选择 \(\text{lazy}(k)\gets\text{lazy}(k)+v\)，代表这段区间已经加过 \(v\) 了

  void add(int k,int l,int r,int v){
      S[k] += (r - l + 1) * v;//这段区间所有值都+v,总共加了(r-l+1)个v
      lazy[k] += v;
  }
  

• 当我们在查询和修改中遇到一个有懒标记的点 \(k\) 时，由于其子树内部的值还未被更新，我们需要将懒标记的影响下传到子树中，并将懒标记清空

  void pushdown(int k,int l,int r){
      //向下一层传递懒标记
      add(ls,l,mid,lazy[k]);
      add(rs,mid+1,r,lazy[k]);
      lazy[k] = 0;
  }
  

• 区间加

  void plu(int k,int l,int r,int x,int y,int v){
      if(x <= l && r <= y) return add(k,l,r,v);//若k对应的区间呗[x,y]包含，打上懒标记就走
      pushdown(k,l,r);
      if(x <= mid) plu(ls,l  ,mid,x,y,v);
      if(y >  mid) plu(rs,mid+1,r,x,y,v);
      pushup(k,l,r);
  }
  

• 区间求和

  记得下传懒标记即可

• 区间乘

  \(\text{Lazy1}[x]\)：\(x\)对应的区间加了多少

  \(\text{Lazy2}[x]\)：\(x\)对应的区间乘了多少

  先乘再加

  void add(int k,int l;int r,int v1,int v2){
      //将 [l,r] 先乘 v2 再加 v1
      S[k] = S[k] * v2 + v1 * (r-l+1);
      lazy1[k] = lazy1[k] * v2 + v1;
      lazy2[k] = lazy2[k] * v2;
      return;
  }