卡特兰数

卡特兰数

太久不写博客了导致我已经快忘了MarkDown语法了TAT

这篇本来应该是一两个月之前就写完的但是因为期末临近拖到现在才动手

但愿我还记得怎么推出来的吧QAQ

数列

\(1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862\)……

通项公式

\[h_n=\frac{1}{n+1}\binom{2n}{n} \]

递推式

\[\begin{aligned} &h_0=1\\&h_1=1\\ &h_{n+1}=h_0h_n+h_1h_{n-1}+...+h_nh_0 \end{aligned} \]

用人话来解释这个公式

1. 前两项人为规定为1
2. 第n项为 以第n-1项和第0项为两端，同时向另一端走，走一步加上一次当前两项的乘积

推导

拿多边形划分举例

这是一个凸n边形，想要求出将这个n边形划分成若干个三角形的方案数

那么现在，我们先将这个n边形用一个三角形划分为\(a\)边形和\(n-a-1\)边形

根据乘法原理，总方案数等于左右两部分拆分方案数之积

而左右两部分又可以继续拆分，直到剩下一个只有一种拆分方案的三角形

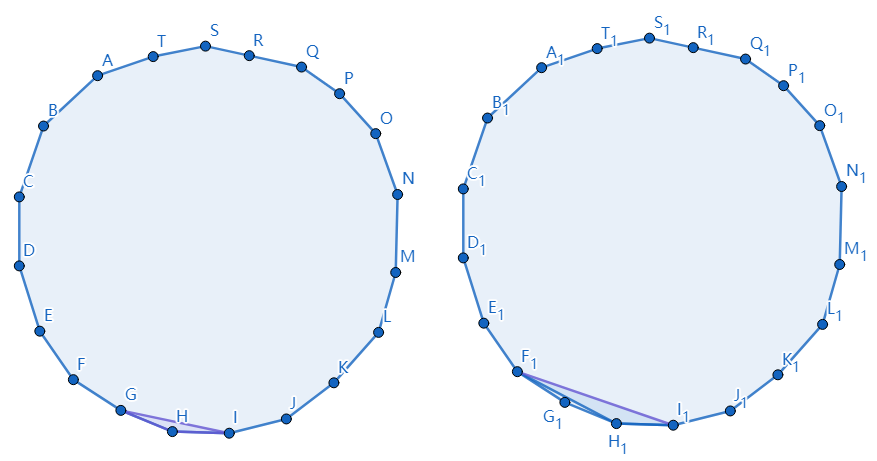
这两张图应该能很好地解释为什么\(C_0\)和\(C_1\)是1：三角形和线段拆分时都相当于不拆分，因此对另一侧没有任何影响，所以将其置为1

示例

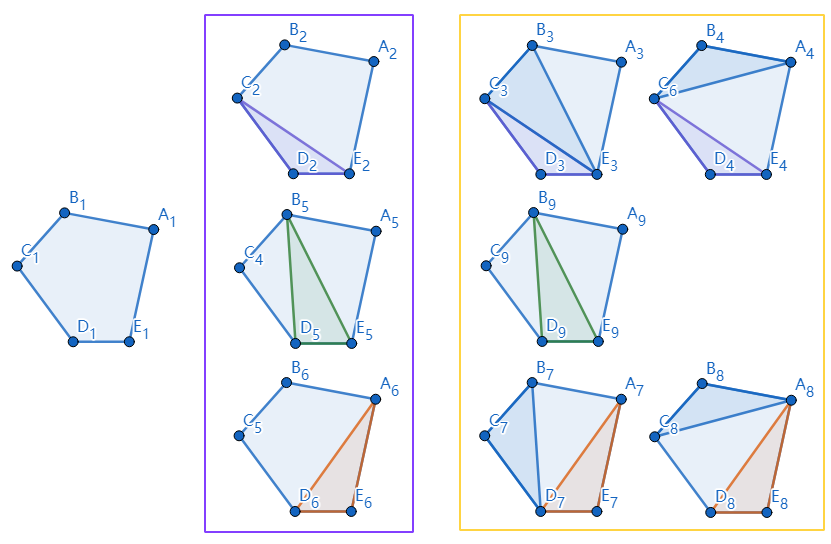
虽然五边形还是不大看得出来但是后面的是真的画不动

所以五边形的拆分方案数是五种

非常好我还记得（

代码实现

//递推式
int Catalan(int n){
	
	//特判
	if(n<3) return 1;
	
	//因为公式里面是h(n+1)，为了计算方便就提前自增1 
	n += 1;
	//初始化 
	int h[20] = {0};
	h[0] = h[1] = 1;
	//从第3项计算到第n项（因为先前自增过1，所以这里的第n项即为所求） 
	for(int i = 2;i<n;i++){
		//每一项的计算 
		for(int j = 0;j<i;j++){
			//st为从前往后走的下标，ed为后往前走的下标 
			int st = j;
			int ed = i - j;
			//相乘后相加
			h[i] += h[st] * h[ed];
		}
	}
	//返回第n项 
	return h[n-1];
}

//通项式
//至于组合数怎么求...推荐用递推式而不是定义式
int Catalan(int n){
	if(n<3) return 1;
	return C(2*n,n)/(n+1);
}