排序算法

来自：http://blog.csdn.net/hguisu/article/details/7776068

排序有内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

 

（一）插入排序：直接插入排序

将第一个数看做已排序列，之后的数插入到已排序列中的正确位置

根据之后的数向已排序列中的插入方式的不同，插入排序又分为直接插入排序（O(n^2)）、二分插入排序（O(nlogn)）

2路插入排序：以第一个元素为准，每一个新元素都向第一个元素的左边或右边已排序的列表中插入，形成两路插入，减少移动次数

（二）插入排序：希尔排序

希尔插入排序实际上是对数据进行处理（分组），即分组进行直接插入排序

首先设计一个增量序列，简单的话可以是d:{n/2,n/4,n/8,......,1}

然后按照增量序列di，将序列中距离为di的元素化在一组进行直接插入排序，直到di取到1，所有元素都在一组中，进行最后一次插入排序

目前还没能给出最好的取出增量序列因子的方法，希尔排序的实效性很难分析

（三）选择排序：简单选择排序

从数据中选择最小的元素依次与第一个、第二个.....元素进行位置交换

改进版本：二元选择排序，即选择剩下数据中最大的和最小的两个元素

（四）选择排序：堆排序

堆排序是一种树型选择排序，是对简单选择排序的有效改进

堆定义：n个元素的序列（k1,k2,...kn），满足下列条件时，称为堆（即数的节点全都小于左右子孩子，或全都大于左右子孩子）

堆排序就是将初始序列，调整存储顺序，使序列成为堆，然后输出堆顶元素，再重新调整存储顺序，使剩下元素序列成为堆，再输出堆顶元素，最后得到排序序列的过程

堆排序涉及到两个问题：

1）初始元素序列建堆

2）堆顶元素取出后，堆调整

n个元素初始建堆的过程：

a)n个节点的完全二叉树，最后一个节点是第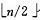个节点的子树，调整该子树，使该子树成为堆

b)找到上一个子树节点，再调整该子树，使其称为堆，依次直到根节点

如图建堆初始过程：无序序列：（49，38，65，97，76，13，27，49）

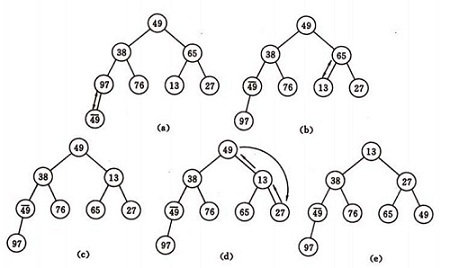
堆顶元素取出后堆调整的方法：

a)将最后一个元素与堆顶进行交换，堆被破坏

b)将根节点与左右子树中的较小者进行交换

c)若与左子树交换：如果左子树堆被破坏，即左子树的根结点不满足堆的性质，则重复方法b)

d)若与右子树交换，如果右子树堆被破坏，即右子树的根结点不满足堆的性质。则重复方法b)

e)继续对不满足堆性质的子树进行上述交换操作，直到叶子结点，堆被建成。

堆排序最坏情况下，时间复杂度也为：O(nlogn )

（五）交换排序：冒泡排序

在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数一次进行比较和调整，大的下沉，小的上冒，则一趟排序后，最大的沉到最下面，之后对上面的n-1个数重新一趟排序

改进：每趟排序加一个标志位，标志每趟排序中最后一次进行数据交换的位置，该位置之后的数据已经排好序

（六）交换排序：快速排序

一趟排序过程：

i指向第一个元素，j指向最后一个元素，k保存第一个元素的值

从j往前找到第一个小于k的值，j移动到此，将此处的值复制到i处

i往后找到第一个大于k的值，i移动到此，将此处的值复制到j处

j继续往前，i继续往后，直到i、j相遇，在i的位置处，放k，则k在最终排序的正确位置上

一趟之后，k的左边和右边分别重复快速排序

（七）归并排序

（八）基数排序