NOIP数学的复习
刷了一个月的蓝紫题,该刷刷黑题绿题,黄题了。。。。。(但我觉得数学好难啊)
单子
1、gcd,lcm,打表
2、exgcd,费马小定理
3、各种筛
4、排列组合,容斥原理,概率与期望
5、卡特兰数
6、快速幂
6、M-R算法
7、素数的常见性质
8、矩阵
9,EXCRT,CRT
下边放板子
(exgcd)
inline int exgcd(int a,int b,int &x,int &y)
{
if (b==0)
{
x=1,y=0;
return a;
}
int ans=exgcd(b,a%b,y,x);
y-=a/b*x;
return ans;
}
(埃氏筛)
inline void assprime(int k)
{
for (int i=2;i<=n;++i) pr[i]=1;
for (int i=2;i<=n;++i)
{
if (!pr[i])continue;
for (int j=2*i;j<=n;j+=i) pr[j]=0;
}
}
(M-R算法)(自己YY的随机化版)
inline bool mr(int k)
{
if (k==1) return 0;
if (k==2) return 1;
for(int i=1;i<=40;++i)
{
int a = rand()%(k-2)+2;
if(fast_pow(a,k-1,k)!=1) return false;
}
for (int i=1;i<=20;++i)
{
int tmp=rand();
tmp=tmp*233333333;
tmp=tmp%(int)sqrt(k+0.5)+(int)sqrt(k+0.5);
if (tmp!=1&&tmp!=k-1&&tmp%k*tmp%k==1) return 0;
}
return 1;
}
excrt
#include<iostream>
#include<cstdio>
#include<queue>
#include<algorithm>
#include<cstring>
//#include<cmath>
#define int long long
using namespace std;
const int maxn=400006;
int n,m,aa[maxn],bb[maxn];
int ra1,ra2,rb1,rb2;
inline int mul(int x,int y,int mod)
{
int ans=0;
y=(y%mod+mod)%mod;
x=(x%mod+mod)%mod;
while (y)
{
if (y&1) ans=(ans+x)%mod;
x=(x+x)%mod;
y>>=1;
}
return ans%mod;
}
inline int exgcd(int a,int b,int &x,int &y)
{
if (b==0)
{
x=1,y=0;
return a;
}
int ans=exgcd(b,a%b,y,x);
y-=a/b*x;
return ans;
}
bool pan;
inline void solve()
{
int fina=rb2-rb1;
int gcd,sx,sy;
gcd=exgcd(ra1,ra2,sx,sy);
int tmp=ra2/gcd;
if (fina%gcd) {pan=1;return;}
int shit=fina/gcd;
sx=(mul(sx,shit,tmp)+tmp)%tmp;
rb1=sx*ra1+rb1;
ra1=ra1*(ra2/gcd);
}
inline int excrt()
{
ra1=aa[1],rb1=bb[1];
for (int i=2;i<=n;++i)
{
ra2=aa[i],rb2=bb[i];
solve();
if (pan) return -1;
}
return rb1;
}
signed main()
{
cin>>n;
for (int i=1;i<=n;++i) {
scanf("%lld%lld",&aa[i],&bb[i]);
}
cout<<excrt();
return 0;
}
卡特兰数
卡特兰数是一种经典的组合数,经常出现在各种计算中,其前几项为 :
1, 2, 5, 14, 42,
132, 429, 1430, 4862, 16796,
58786, 208012, 742900, 2674440, 9694845,
35357670, 129644790, 477638700, 1767263190,
6564120420, 24466267020, 91482563640, 343059613650, 1289904147324,
4861946401452, ...
公式:
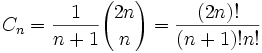
线性递推式子:
C(n)=C(n-1)*((4*n-2)/(n+1));
不用求逆元的记忆化搜索式子
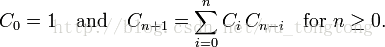


 浙公网安备 33010602011771号
浙公网安备 33010602011771号