矩阵快速幂

矩阵乘法的定义

矩阵 A* 矩阵 B = 矩阵 C

 

                                            

 

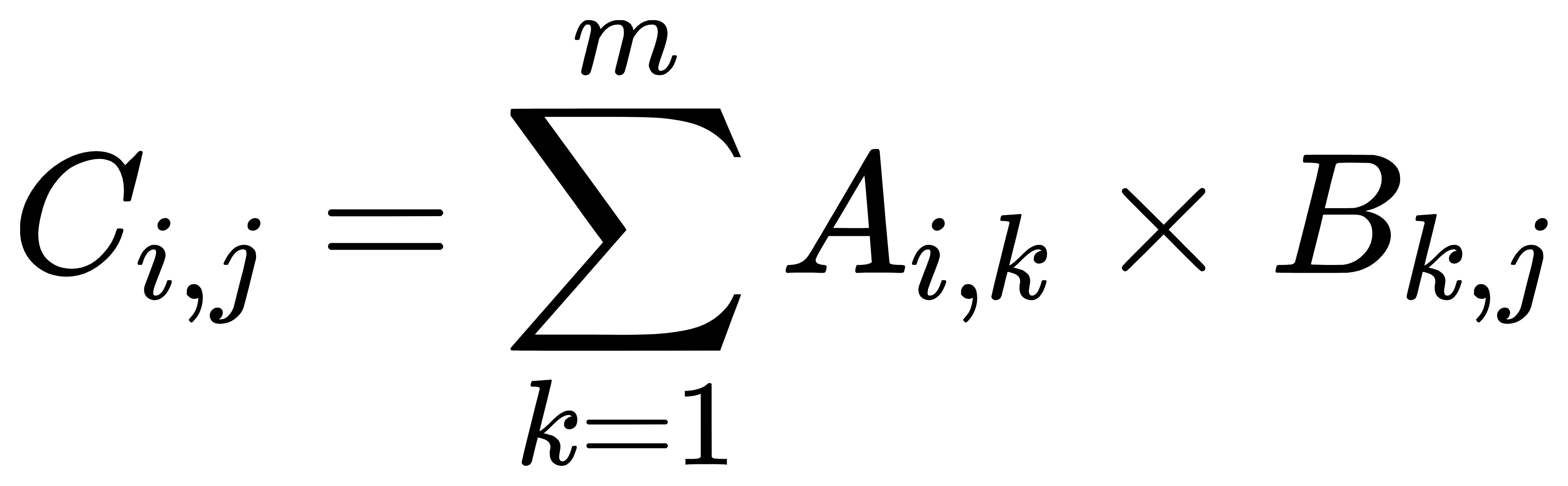
性质：满足结合律，分配率，但不满足交换律

矩阵乘法的特殊情形

矩阵 A 是一个 N*N 的矩阵，矩阵 F 是一个 N*1 的矩阵，设 F1= A*F，发现 F1也是一个 N*1 的矩阵，只有一行元素的矩阵，我们不妨把这些元素看成是一个个变量，而矩阵 F1 的变量通过矩阵 F 的变量的某种关系来实现更新，而这种关系通过矩阵 A 来实现（所以矩阵 A 也可以称作是系数矩阵？）

比如斐波那契数列，f[n+2]=f[n+1]+f[n]，得出转移矩阵

 应用

上述的矩阵乘法的特殊情形常用于递推式，特别是当递推的次数达到一定的数量级，就可以用矩阵快速幂大大减少运算量，避免一些重复的计算。

矩阵快速幂

对于矩阵 F[n]=F[n-1]*A，可求出：

F[n=F[0]*pow(A,n)

A 的 n 次方需要一个 A 一个 A 来连乘获得吗？快速幂啊！

这样时间复杂度就降到了 log(n) 级，最终再乘上内部矩阵乘法所需的时间（三重循环）来得到最终的复杂度。

D. Magic Gems

n<=1e18，m<=200

我们要求空间为 n 的物品摆放方案数。

设 dp[i] 为空间为 i 的方案数，容易得出状态转移方程：

dp[i]=dp[i-1]+dp[i-m](i>=m)

令矩阵 F[n]={f[n],f[n-1],...,f[n-m+1]}，F[n-1]={f[n-1],f[n-2],...,f[n-m]}

F[n]=F[n-1]*A

解得 A

 

 

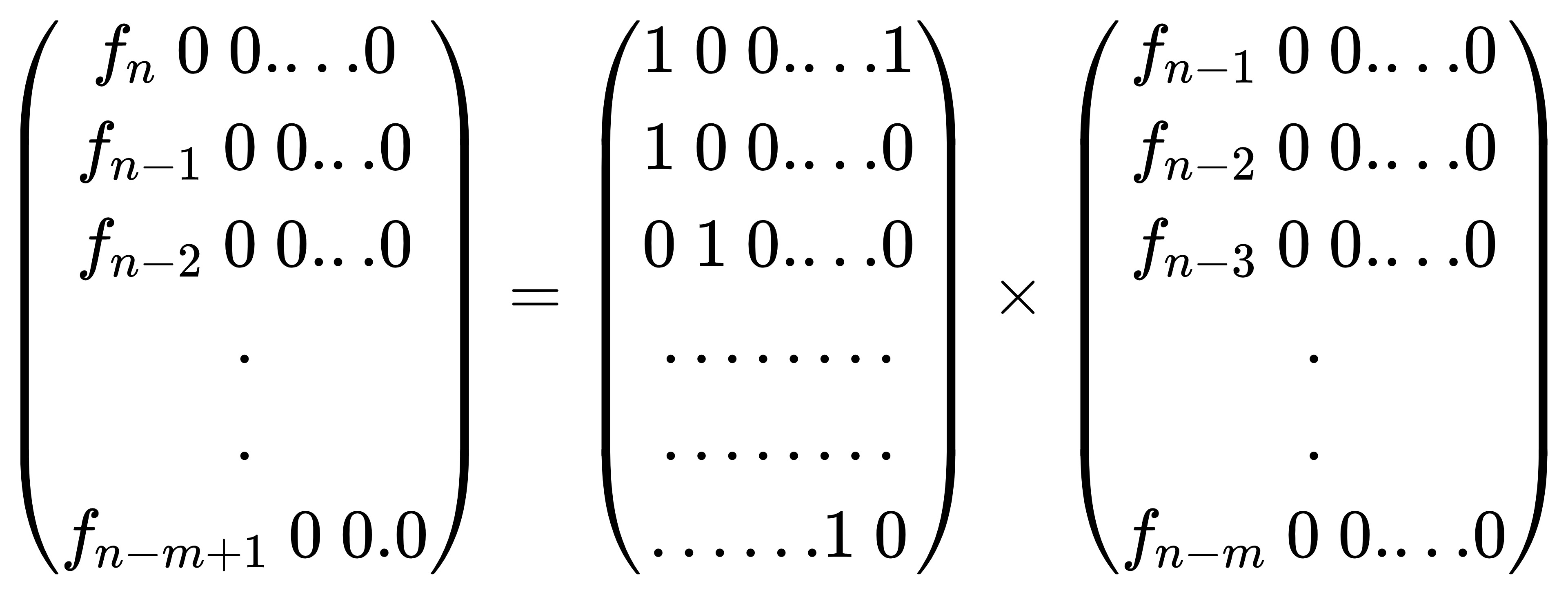
由此可得，F[n]=F[m-1]*pow(A,n-m+1)

而矩阵乘法可以用快速幂优化，时间复杂度为 m*m*m*log(n)

暴力又优雅呢！

#include<bits/stdc++.h>
#define int long long
#define mod 1000000007
using namespace std;
const int N=1e6+10;
int n,m,t,k,qq;
struct Mat{
    int a[110][110];
    Mat(){
        memset(a,0,sizeof(a));
    }
};
Mat operator*(Mat A,Mat B){
    Mat ret;
    for(int i=0;i<m;++i)
        for(int j=0;j<m;++j){
            int tmp=0;
            for(int k=0;k<m;++k)
                tmp=(tmp+A.a[i][k]*B.a[k][j])%mod;
            ret.a[i][j]=tmp;
        }
    return ret;
}
Mat power(Mat mat,int k){
    Mat ret;
    for(int i=0;i<m;++i)
        ret.a[i][i]=1;
    while(k){
        if(k&1) ret=ret*mat;
        mat=mat*mat;k>>=1;
    }
    return ret;
}
void solve(){
    cin>>n>>m;
    if(n<m) {cout<<1<<endl;return;}
    Mat mat;
    mat.a[0][0]=mat.a[0][m-1]=1;
    for(int i=1;i<m;++i) mat.a[i][i-1]=1;
    mat=power(mat,n-m+1);
    int ans=0;
    for(int i=0;i<m;++i) ans=(ans+mat.a[0][i])%mod;
    cout<<ans<<endl;
}
signed main(){
    int T=1;
    //cin>>T;
    while(T--) solve();
    return 0;
}