生成函数
友情提示：不是闲来无事千万别学！！！
看了网上一些博文，总觉得写得很乱。最近刚好学习了相关内容，决定亲自动手写一篇。
首先你要明白，一些知识易于理解难以应用，而另一些易于应用难以理解。生成函数属于后者。
网上甚至一些书籍对生成函数的介绍大部分都是有问题的，这也导致初学者在学习生成函数时困难重重。
首先请你百度生成函数，并阅读完百度百科的介绍。
好，你现在应该一知半解，现在再看看这篇的介绍。
嗯，现在你阅读完了。那么 此刻你应该对生成函数的应用场景和求法有初步的理解。
不同的生成函数有不同的求法，我们将其分类。
而网上写的博文往往跳过了生成函数的应用场景与求法，直接分类讲一大堆 “没有用的知识” 。在工科的世界，这很愚蠢！！！
而工科偏重理论，也很愚蠢！！！
我说这么多就是想说：网上写的生成函数真不是人能看懂的！！！
前置知识
多项式
表达式：
以下内容仅需了解：卷积（多项式乘法），多项式求逆，多项式ln，多项式exp，牛顿迭代...
（当然，这是不可能的）
- 分治+NTT
比较厉害的一个技巧。
- 给定 n 个一次多项式 ai + bix，求
- n<=105
暴力卷积，时间复杂度 > O(n2)的......
原因就在于卷着卷着次数会不断变大。
想象一下，我们平时做多个数的乘法，没有人会去顺序一个一个乘吧......
那可以用类似分治的办法，对于每个区间将左右合并起来。
时间复杂度：T(n)=2T(n/2)+O(nlogn)=O(nlog2n)
具体的实现可以用 vector 存多项式，空间复杂度是 O(nlogn)的。
类似的，还可以拓展出分式求和：
给定 n 个一次多项式 ai+bix，求 
如果直接求逆是 O(n2logn)的，
同上，对于每个区间维护分子和分母，最后再求逆算答案。
时间复杂度 O(nlog2n)，空间复杂度 O(nlogn)。
Taylor 展开
其实这个不是重点。
然后有个背下来经典的东西：
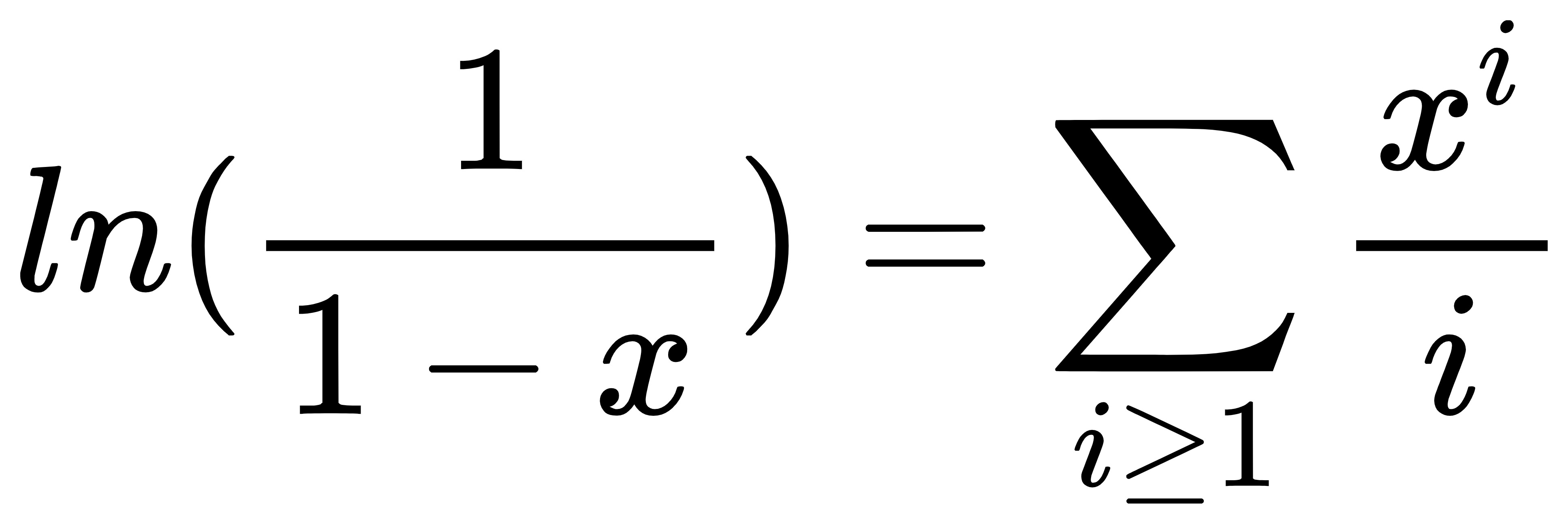
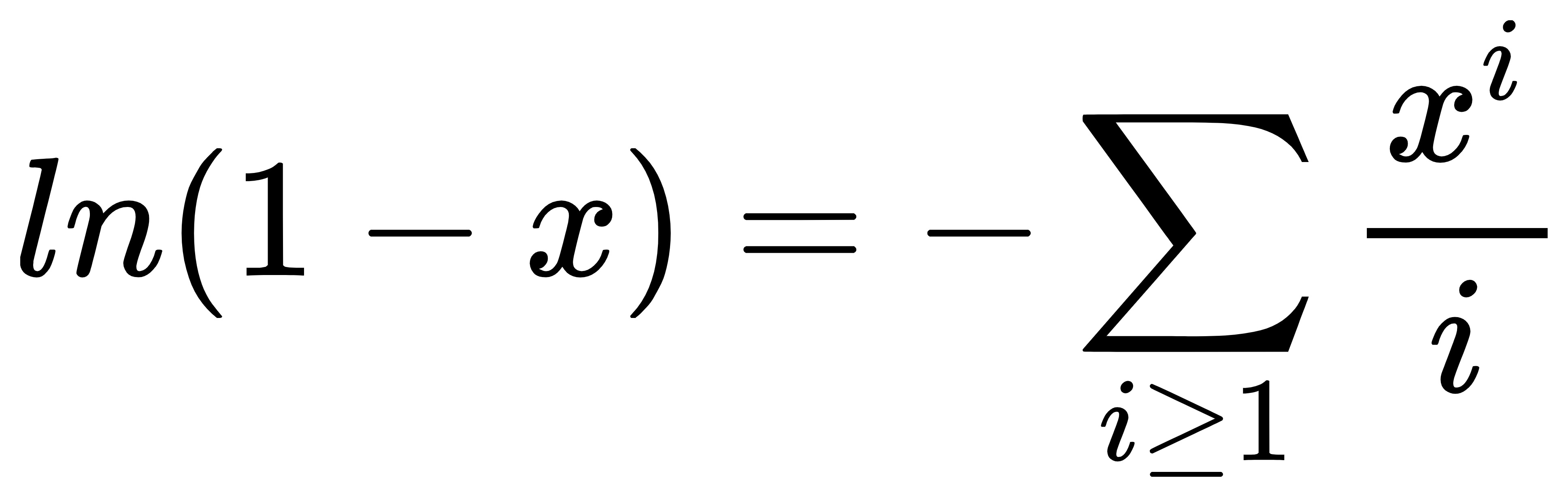
可以直接泰勒展开，不过也可用别的方法推：
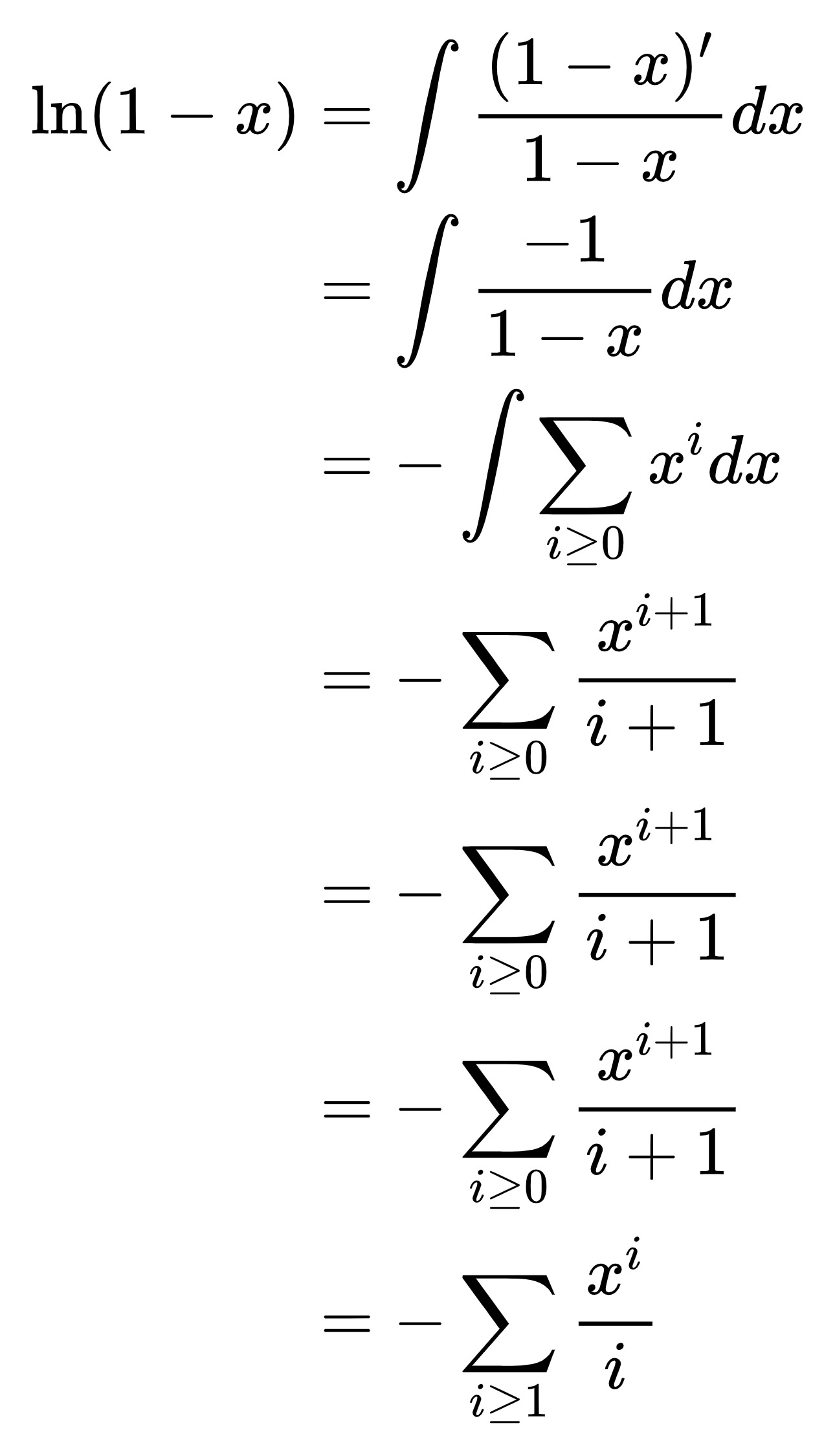
广义二项式定理
我们都知道喜闻乐见的二项式定理：
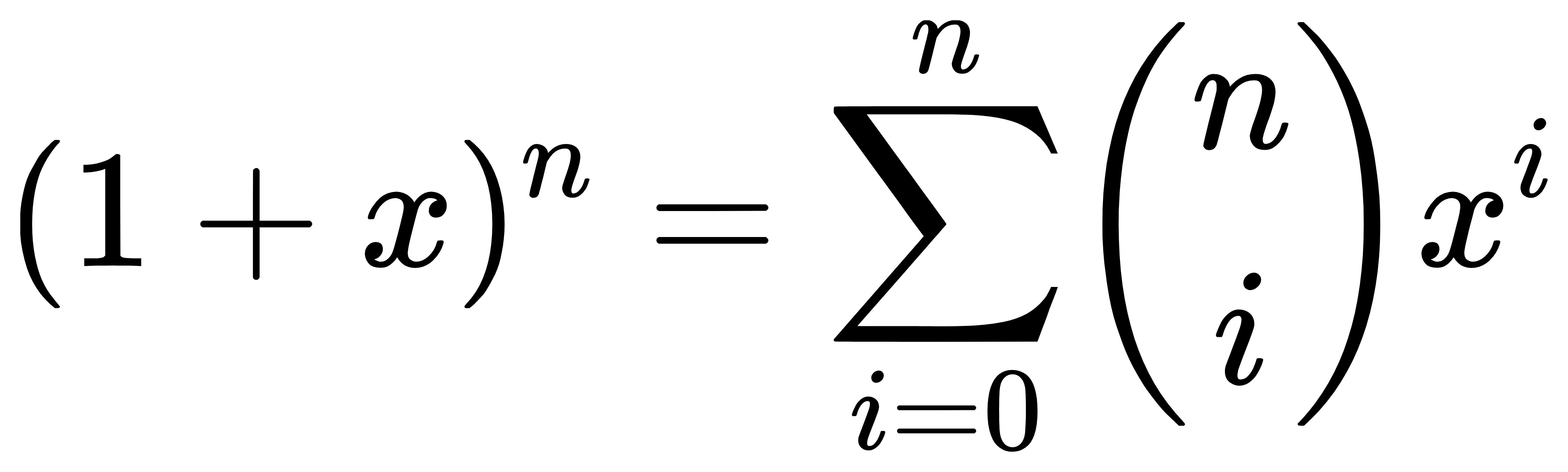
但有时候，我们想让这个 n 变成负数甚至小数咋办？
设 
我们有 
解释一下求导：
...
带入，得：
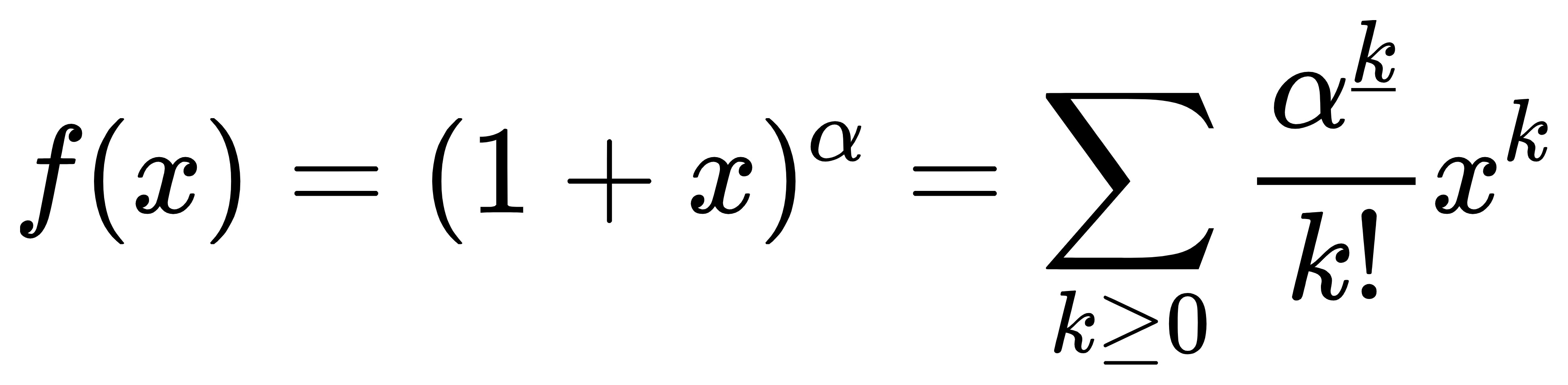
啊哈，于是我们还能定义拓展的组合数 
普通型生成函数（OGF）
我们现在有一个序列 { fi }
把序列扔到多项式的系数上，就能得到一个对应的多项式：
- 注意： x 只是形式的自变量，并没有实际意义，可任意赋值。
当然，更严谨一点，x 的取值必须要使 F(x) 收敛，不过暂不考虑。
下面来介绍一些变换。
k阶前缀和
现有一个数列 {ai} 和它的生成函数 A(x)，求出它的前缀和 {bi} 。
那么 {bi} 的生成函数是啥呢？
那又多了一个新的多项式 
。
事实上，当 -1≤x≤1时，
。
也就是生成函数的封闭形式。
那要怎么变回来呢？
没事，看广义二项式定理！
当然，要求出 k 阶前缀和也很简单了：
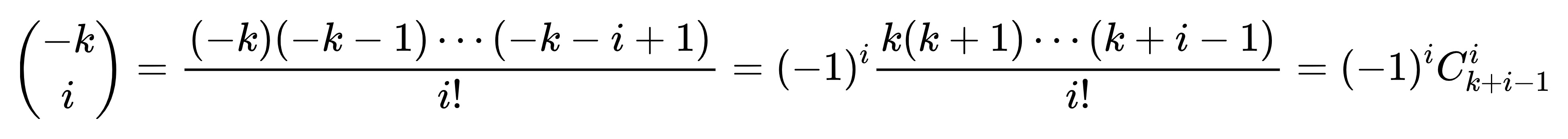
拿 f 和 A 卷一下就行了，O(nlogn)。
平移、伸缩与单位根反演
- 平移
向右平移：直接乘个 xk 就好了。
向左平移：乘个 x-k，但还要先把多余的项减掉。
套上求导，就会出现神奇的事情：
- 伸缩
显而易见呐！
就好像是把系数往后伸缩了一样。
- 单位根反演
第二个能用 A(-x) 是因为 (-1)2=1。
那什么时候 x 满足 xk=1 呢？
聪明的同学们一定都想到了单位根。
这玩意叫单位根反演，拿等比数列随便证一下就行了：
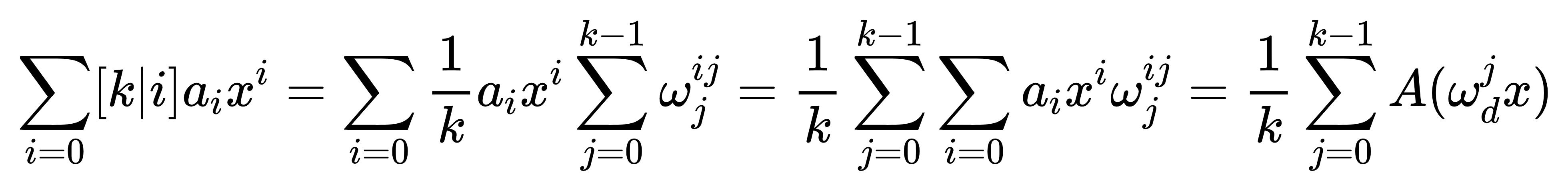
生成函数与数列通项（上）
扔一个简单的递推数列，比如斐波那契数列（fn=fn-1+fn-2 (n>1)，f0=0，f1=1），想求它的通项公式
相信大家都知道矩阵乘法。（然而这不是重点
相信大家都知道特征方程。（然而不详细解释
相信大家都知道，生成函数也可以拿来推这个？
设 F(x) 为 {fn} 的生成函数，显然有：
原因也很简单：
n=1 的时候还要在补个 x，是边界条件。
然后把 F(x) 提到左边：
这个怎么求呢？我们一会儿再说......
先来看一道更加奇妙的问题......
P4451 [国家集训队]整数的lqp拆分
数列 {fn} 满足 fn = fn-1 +fn-2 (n>1)，f0=0，f1=1 。
对于 n 的整数拆分，即满足 a1+a2+a3+...+am=n 且 
的数组 an，定义其权值为S(a)=fa1+fa2+...+fam
- 求 n 的所有整数拆分的权值之和对 109+7 取模的值。
- n<= 10100000
首先解释一下这个奇怪的整数拆分：
如果设选一个数的生成函数为 F(x)=f0+f1x+f2x+...
则整数拆分的生成函数为 G(x)=1+F(x)+F(x)2+...
其中 F(x)k 就是拆成 k 个数的方案数。
（其实这是第二章的内容）
那当然把它们变成封闭形式：
下面来说说怎么把这个奇奇怪怪的封闭形式还原成多项式。
先把它变得好看一点：
有二次，显然是没办法直接用拓展二项式做的。
不过联想一下初二的数学知识，我们可以把分式裂开成两个一次的。
经过一番轻松的解方程能得到：
这个形式不太好看，给它乘个常数再变一变：
现在拿它当分母，再用初二的数学知识待定系数：
解一解：
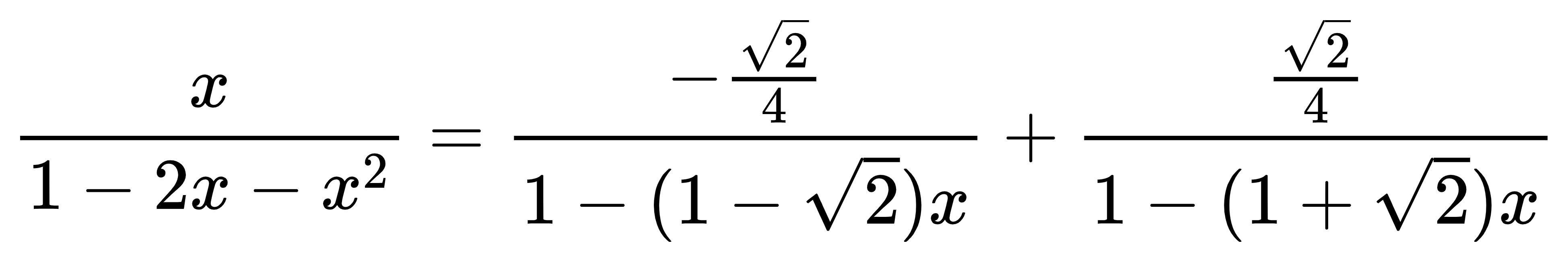
这样就能算了：
是不是很神奇？
当然斐波那契数列也是同样的......
生成函数与数列通项（下）
------------恢复内容结束------------
