二项式定理

转载请注明出处，部分内容引自 Jμdge's class大神 的博客

一般二项式定理

二项式定理我们在高中阶段已经初步接触，

                    

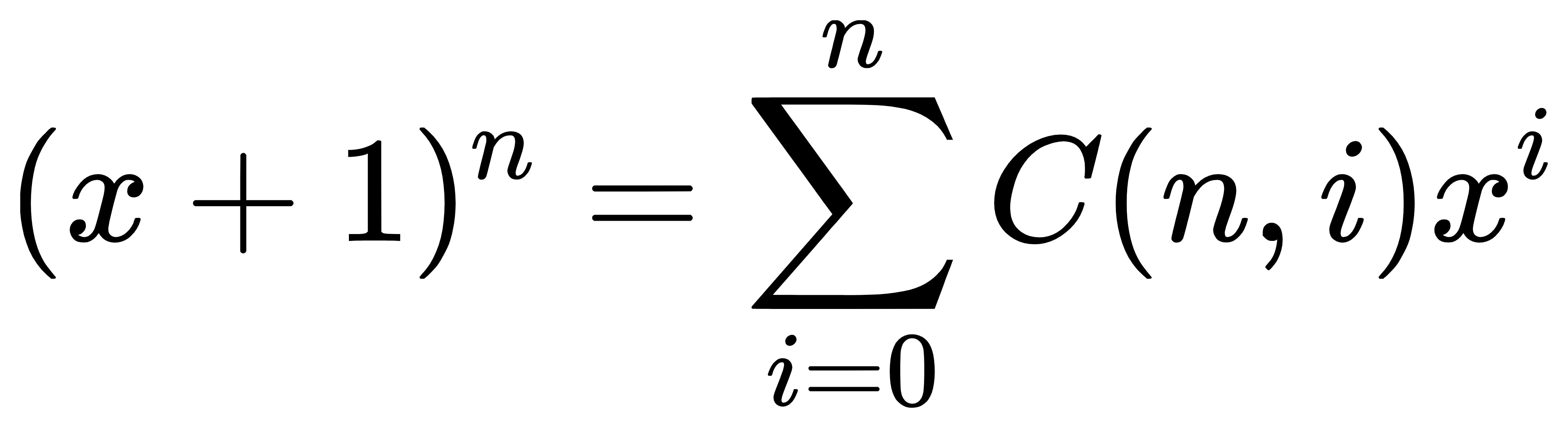
其中 n 为整数

                    

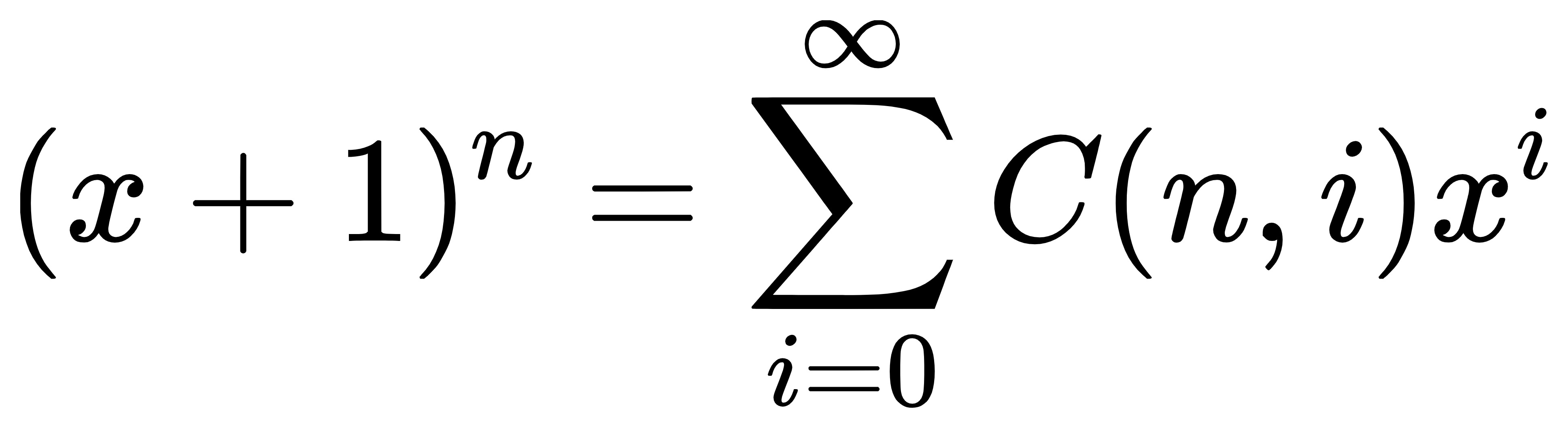
 该式与上式等价，因为当 i > n 时，组合数 C(n,i) 为 0.

这样我们就得到了形式更为一般的二项式定理

指数为负的二项式定理

现在我们考虑一下 (x+1) 的指数推广到 负数 的情况

这个时候其实也有：

                     

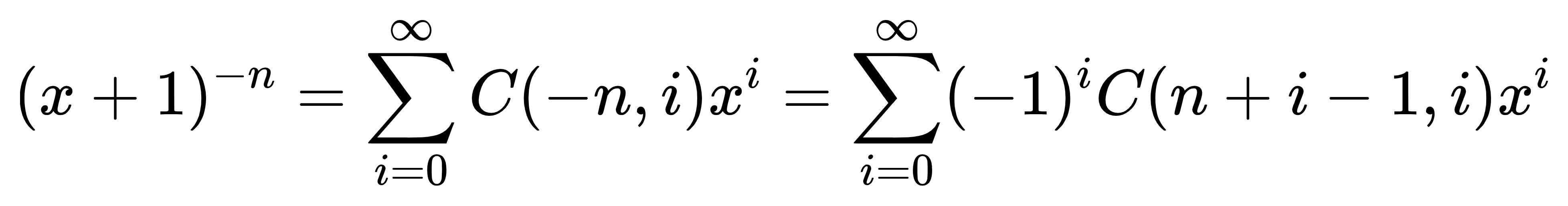
咦，组合数还有负的么？

有。由组合数的定义，得：

                     

 等价变换：

                    

                     

 that's it !

也许你已经看过上面的式子了。

把上述式子整理一遍，得出：

　　　　　　　　　　　　　　

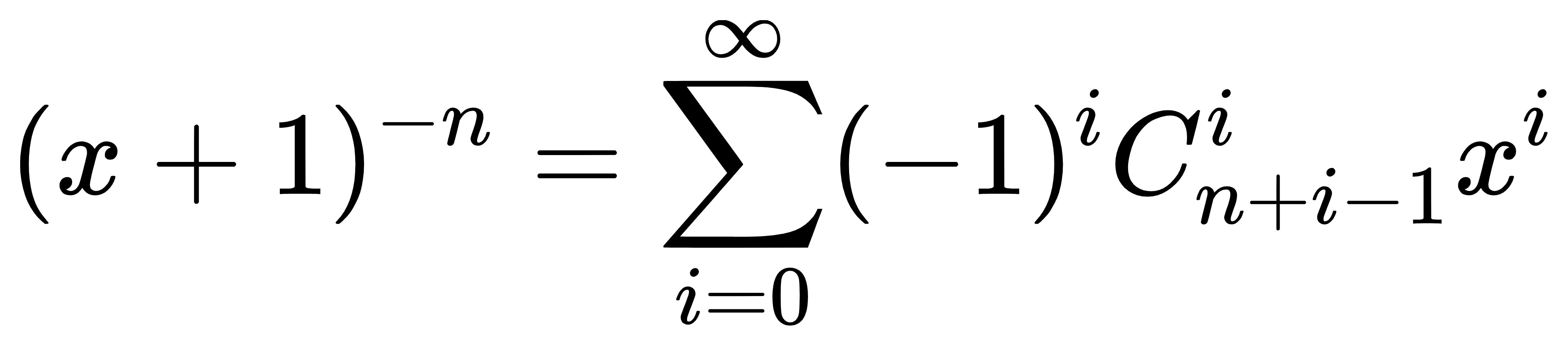
 当加号变为减号

（在这里我们略去 n 为负数的情况）

首先的话，我们考虑将上面式子中的 x 取负，那么原式就变成了：

　　　　　　　　　　　　　　

 即：

　　　　　　　　　　　　　　

这个式子有没有感觉在哪里见过？

这时，如果我们把 n 变为 -n，那么式子变为：

　　　　　　　　　　　　　　

 也就是说两个正负号抵消掉了。

这个式子其实很有用处，它会在你学习生成函数的时候大展身手

 

二项式定理的一般形式

其实上面讲了这么多都是二项式定理的特殊形式（但其实都是比较常见+实用的）

现在说说它的一般形式：

　　　　　　　　　　　　　　

 这个东西可以理解为有 n 堆物品，每堆里面有 x 和 y，每堆只能选一个，要求选择的所有方案之和

具体证明就毋须多言了，上面已经证了一大堆了

 

关于广义二项式定理

其实广义二项式定理就是上面的那个式子，我们只要将指数 n 的定义域改成实数即可

也就是说，广义二项式定理对于实数也成立，也就是：

　　　　　　　　　　　　　　

 而关于 C(α,i) 的值依然是按照之前组合数的定义

 

二项式与组合数的关系

这部分很多同学都很熟悉了。

1.把二项式定理的 x y 变为 1,1，式子变为：

　　　　　　　　　　　　　　

还记得二项式系数吗？

简单说一下，从 n 个物品选择任意个的方案数之和 = 2n

2.把二项式定理的 x y 变为 1,-1，式子变为：

　　　　　　　　　　　　　　

 选择 奇数个的方案数之和 = 选择 偶数个的方案数之和

这里似乎有点秃然？

仍然从二项式定理的角度考虑：共有 n 个，第一种选择 x 个，第二种选择 y 个。根据容斥原理，C(n,1)-C(n,2)+C(n-3)...+C(n,n)=1

C(n,0)=1，两者相减为0，得证。

应该还有其他的理解方式，我这里采用 二项式定理+容斥原理 的方式证明。

 

总结

二项式定理很有趣，虽然学起来很简单，但是你很容易经常看到它的身影，到时候别忘记再翻开这篇博文，或许你会有新的收获~