博弈论

博弈之道，包罗万象。

本文有关博弈内容只涉及部分 ACM 的应用。

一、必胜点和必败点

P点：必败点，在双方都聪明无比的情况下。

N点：必胜点，在双方操作都正确的情况下。

有向图的核

给定一张DAG图<V,E>，如果 V 的一个点集 S 满足：

S是独立集（集合内的点互不相通）
集合 V - S 中的点都可以通过一步到达集合 S 中的点（V - S指 S 在 V 中的补集）

则称S是图 V 的一个核。

结论：核内节点对应 SG 组合游戏的必败态

因为 Alice 当前的棋子在 S 中，由于 S 是独立集，也就意味着 Alice 只能将棋子从 S 移动到 V - S

而 Bob 又可以通过一步移动将棋子从 V - S 移动到了 S，这样 Alice 就好像是被支配了一样，被迫把棋子到了没有出度的必败节点，Alice 必败，Bob必胜！

几个性质

所有的终止位置都是必败点P（我们认为这个是公理，即所有推导都在这个性质成立的基础上进行）。
从任何一个必胜点N操作，至少有一种方法可以达到一个必败点P。
从一个必败点P出发，只能够到达一个必胜点N。

二、无偏博弈

无偏博弈是一类任意局势对于游戏双方都是平等的回合制双人游戏。平等的含义是当前的所有可行的走法仅仅只依赖于当前的局势，而与当前谁移动无关。换而言之，两个人除了先后手的区别之外就不存在任何区别。除此之外，还需要满足一个性质：

完全信息，任何一个游戏者都能够知晓整个游戏状态。
无随机行动，所有的行动都会转移到一个唯一确定的状态。
在有限步内游戏会终止，此时有唯一的胜者。

三、常见模型

巴什博弈(Bash Game)
威佐夫博弈(Wythoff Game)
尼姆游戏(Nim Game)
Anti - SG游戏
Multi - SG游戏
Every - SG游戏
翻硬币游戏
树上删边游戏

巴什博弈

基本问题

有一堆石子，总个数是n，两名玩家轮流在石子堆中拿石子，每次至少取一个，至多取m个。取走最后一个石子的玩家为胜者。判定先手和后手谁胜。

解决方法

如果(m+1)|n则先手必败，否则先手必胜。

证明

假设(m+1)|n，那么假设先手拿了x个，那么后手必定可以拿走(m+1)-x个，这样无论先手怎么拿，剩下的石头都是m+1的倍数。那么最后一次取的时候石头个数必定还剩下m+1个，无论先手拿多少个，都会剩下石头，此时后手必定可以将剩下的所有石头取光从而获胜。

否则的话，先手可以取走n%(m+1)个石头，此时模型转换为了先手面对(m+1)|n个石头的情况，也就是后手必败，即先手必胜。

eg：HDU1846 Brave Game

威佐夫博弈

基本问题

有两堆石子，石子数可以不同，两人轮流取石子，每次可以在一堆中取，或者从两堆中取走相同个数的石子，数量不限，取走最后一个石子的人获胜，判断先手是否必胜。

解决方法

一共只有两堆石子，我们可以把问题放到二维坐标系上，设x,y分别对应两堆石子的数量。

模拟显然发现（0,0）先手必败，我们将先手必败节点称为 奇异节点。

可以发现奇异节点上下左右四个节点，以及右上和右下的两个节点都不是奇异节点。

也就意味着如果 Alice 不在奇异节点上，那么 Alice 可以通过一步操作到达奇异节点，那么 Alice可以通过一步操作到达奇异节点，把奇异节点留给 Bob，这样 Bob必败。

我们可以发现（1,2），（3,5）等等也都是奇异节点。

经过奇异节点的 3 条直线上的点，都能通过一步到达奇异节点。

发现这就建立起了一个有向图的核的模型。

考虑引入 Beatty定理

如果两个无理数 a,b 满足：

$\frac{1}{a}+\frac{1}{b}=1$ 那么对于两个集合 A,B：A={⌊na⌋}，B={⌊nb⌋}，n € Z有下面两个结论：A ∩ B = Ø，A ∪ B=N+打表发现B_i- A_i=i

可得 b=a+1，带入 $\frac{1}{a}+\frac{1}{b}=1$ 解得 $a=\frac{\sqrt{5}+1}{2},b=\frac{3-\sqrt{5}}{2}$

最终得出威佐夫结论：假设两堆石子为(a,b)（其中a<b)

那么先手必败，当且仅当 $(b-a)*\frac{\sqrt{5}+1}{2}=a$

其中的 $\frac{\sqrt{5}+1}{2}$ 恰好就是黄金分割数1.618。What a coincidence!

斐波那契博弈

基本问题

有一堆个数为 n(n>=2)的石子，游戏双方轮流取石子，规则如下：

先手不能在第一次把所有的石子取完，至少取 1 颗；
之后每次可以取的石子数至少为 1，至多为对手刚取的石子数的 2 倍。

约定取走最后被一个石子的人为赢家，求必败态。

解决方法

先手必败，当且仅当石子数为斐波那契数

先证明必要性，斐波那契数一定先手必败，可以用数学归纳法，大致思路就是一定能拆成两堆斐波那契数，不论先手怎样取，后手总能取到最后一颗

然后证明充分性，由定理：任何正整数可以表示为若干个不连续的Fibonacci数之和，那么就回到了斐波那契数列里

具体证明见：斐波那契博弈（Fibonacci Nim）

SG函数

前置知识：Mex运算

设 S 表示一个非负整数集合。定义 mex(S) 为求出不属于集合 S 的最小非负整数的运算，即：mex(S)=min{x}，x 属于自然数，且 x 不属于 S。

SG函数

SG函数是对游戏图中每一个节点的评估函数。

规定游戏终点的 SG 函数值定为 0，即 SG（终点）=0。

在有向图游戏中（任何一个博弈都可以转换为一个有向图游戏），对于每个节点 x（局面），设从 x 出发共有 k 条有向边（合法的操作），分别到达节点 y₁,y₂,...,y_k（下一个局面），定义 SG(x) 为 x 的后继节点（注意只是一层的后继节点）y₁,y₂,...,y_k的 SG 函数构成的集合再执行 mex(S) 运算的结果，即：

SG(x)=mex({SG(y₁),SG(y₂),...,SG(y_k)})

如图所示：

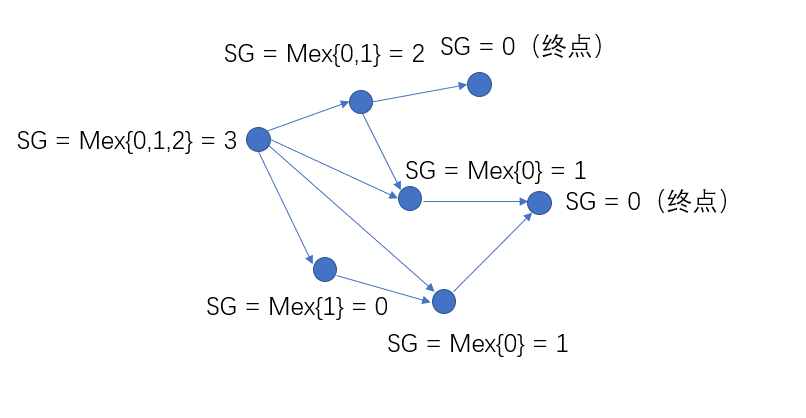
特别的，整个有向图游戏 G 的 SG 函数值被定义为有向图游戏起点 s 的 SG 函数值，即 SG(G)=SG(s)。

我们发现若 SG(x)=0 则为必败状态，若 SG(x) $\neq$ 0，则为必胜状态。（若非零说明这个点直接指向了0，也就意味着可以到达必败状态，是必胜状态）SG定理

两个SG函数的性质：

（1）对于任意的局面，如果它的 SG 值为 0，那么它的任何一个后继局面的 SG 值不为 0.

（2）对于任意的局面，如果它的 SG 值不为 0，那么它一定有一个后继局面的 SG 值为 0.

SG（Sprague — Grundy）定理：所有一般胜利下的公平组合游戏都能转化成尼姆数表达的尼姆堆博弈，一个博弈的 尼姆值 定义为这个博弈的等价尼姆数，即：对于当前游戏 X，它可以拆分成若干个子游戏 x₁,x₂,...,x_n 那么 SG(X) = SG(x₁)⊕SG(x₂)⊕...⊕SG(x_n)。

对于由 n 个有向图游戏组成的组合游戏。设它们的起点分别为 s₁,s₂,...,s_n（好多个起点，有好多个博弈图），则当且仅当 SG(s₁)⊕SG(s₂)⊕...⊕SG(s_n) $\neq$ 0时，这个游戏为先手必胜。

也就意味着，我们将原本需要考虑博弈图的所有点，复杂度较高，但是我们通过SG函数，变成了只需要考虑起点即可。

证明方法类似尼姆游戏，略。

转换为 Nim 游戏

事实上，每一个简单SG-组合游戏都可以完全等效成一堆数目为 K 的石子（Nim游戏），其中 K 为该简单游戏的 SG 函数值。这样的等效是充要的。

定义游戏的和：考虑任意多个同时进行的SG-组合游戏，这些SG-组合游戏的和是这样一个SG-组合游戏，在它进行的过程中，游戏者可以任意挑选其中的一个 单一游戏 进行决策，最终，没有办法进行决策的人输。

定理：在我们每次只能进行一步操作的情况下，对于任何的游戏的和，我们若将其中的任一单一SG-组合游戏换成数目为它的SG值得一堆石子，该单一SG-组合游戏的规则变成取石子游戏的规则（可以任意取，甚至取完），则游戏的和的胜负情况不变。

这个定理告诉我们，在考虑游戏的和时，每一个单一游戏的具体细节是可以被忽略的，我们所关心的只是SG函数值。所以我们可以将组成它的所有子游戏全部换成相应数目的一堆石子。这样，所有的游戏的和都等价成一个 Nim 游戏。

有向图游戏的和

设 G₁,G₂,...,G_m是 m 个有向图游戏。定义有向图游戏 G，它的行动规则是任选某个有向图游戏 G_i，并在 G_i 上行动一步。G 被称为有向图游戏 G₁,G₂,...,G_m的和。

有向图游戏的和的 SG 函数值等于它包含的各个子游戏 SG 函数值的异或和，即：

SG(G) = SG(G₁)⊕SG(G₂)⊕...⊕SG(G_m)

定理1：有向图游戏的某个局面必胜，当且仅当该局面对应节点的SG函数值大于0。

定理2：有向图游戏的某个局面必败，当且仅当该局面对应节点的SG函数值等于0。

我们只需要判断一下 SG(G) 即可。

基本问题

给定 n 堆石子以及一个由 k 个不同正整数构成的数字集合 S。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S，最后无法操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

解决方法

每一堆输入的石子数就是每一堆的起点，答案就是所有起点的 SG函数值异或和。

假设某一堆有 10 个石子，S={2,5} 那么博弈图就是从 10 开始连边，如下图所示。

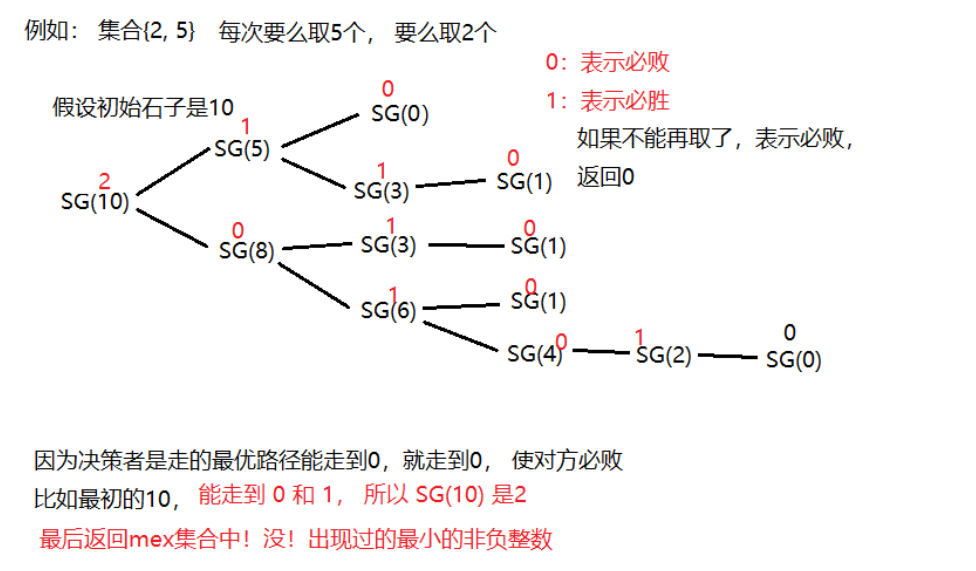
本题的连边方式就是从集合 S 中选择一个数往下走

我们直接记忆化搜索 SG 函数即可。

Anti-SG 游戏（走完最后一步者输）

Anti-Nim

基本问题

有 n 堆石子，两个人可以从任意一堆石子中拿任意多个石子（不能不拿），拿走最后一个石子的人失败。问谁会胜利

看上去好像颠覆了 SG游戏的规则，胜利的条件反了。

先给出结论

先手必胜当且仅当：

（1）所有堆的石子数为 1 且游戏的SG值为 0。

（2）有些堆的石子数大于 1 且游戏的SG值不为 0。

prove：

游戏可以被分为三种情况：

1.每堆只有一个石子

每一堆石子的 SG值显然是这堆石子的个数，每一堆石子就是一个起点，故：

当总异或值（游戏和的SG值）为 0 时（有偶数堆），先手必胜

否则，必胜。

2.只有一堆石子数大于1，先手必胜

如果除去这堆的异或和为0，就把这堆剩下一个，这样就回到情况1

否则把这堆取完，同样类同情况1

3.至少存在两堆石子数大于 1

当异或和为 0 时，先手必败

当异或和不为 0 时，先手必胜

当异或和为 0 时，由于至少有两堆石子的数目大于 1，则在先手决策完之后，必定至少有一堆的石子数大于 1，且SG值不为 0，这时对于此时的先手（比赛开始前的先手）到达了只有一堆石子数大于 1 的情况，先手必胜。也就意味着此时，无论先手如何决策，都只会将游戏带入到先手必胜局，所以先手必败。

当异或和不为 0 时，由于还有至少两堆石子的数目大于 1，则先手通过一次操作将 SG值变为 0 即可，局面就变成了上面那种先手必败的局面送给后手，也就意味着先手必胜。

综上，定理得证。

Anti-SG游戏

之前内容关于 Anti-Nim 游戏的结论推导只对 Anti-Nim 这一简单游戏成立。因为我们在证明 SG函数性质时，用到了这样一个性质：SG值为0的局面不一定为终止局面。

也就是说 Anti-Nim 游戏的结论并不适合所有的 SG 游戏。

因此对于我们再来研究一下普通的 Anti-SG 游戏。

定义 Anti-SG 游戏：决策集合为空的游戏者获胜，也可以理解为将所有集合变为空的游戏者即为失败。其余规则与普通的 SG 游戏相同。

为了解决这一问题，定义 SJ 定理：

对于任意一个 Anti-SG 游戏，如果我们规定：当局面中所有的单一游戏的SG值为 0 时，游戏结束，则先手必胜当且仅当：

游戏的 SG函数值不为 0 且游戏中某个单一游戏的 SG函数值大于1。
游戏的 SG函数值为 0 且游戏中没有任意一个单一游戏的 SG函数值大于1。

由于证明过程略显冗长，感兴趣的读者可以点击这里。

Multi-SG游戏

Multi-Nim 游戏

我们还是先从最简单的 Multi-Nim 游戏出发

有n堆石子，两个人可以从任意一堆石子中拿任意多个石子（不能不拿）或者把一堆数量不少于 2 的石子堆分为两堆不为空的石子堆，没法拿的人失败。问谁会胜利。

Multi-Nim 游戏一共有两种操作，其中操作一很明显就是普通的 Nim 游戏。操作二实际上就是把一个单一游戏分为两个单一游戏，根据 SG 定理，我们知道两个游戏的异或和就是这个单一游戏拆分前的SG函数值，作为一个后继状态。

eg1.1：SG（3）的后继状态有{(0),(1),(2),(1,2)}也就是这堆有 3 个石子的石子堆，可以拿走或者分开等四种情况，他们的SG值分别为{0,mex{0}=1,mex{0,1}=2,mex{0,1,2}=3}，因此SG(3)=mex{0,1,2,3}=4

Multi-Nim游戏的性质：

$SG(x)=\left\{\begin{matrix} x-1 (x mod 4 = 0) \\ x (x mod 4= 1 or 2) \\ x+1 (x mod 4 = 3 ) \end{matrix}\right.$

Multi-SG游戏

因此我们定义 Multi-SG 游戏：

Multi-SG 游戏规定，在符合拓扑原则的前提下，一个单一游戏的后继可以为多个单一游戏。
Multi-SG 其他规则与SG游戏相同。

可以理解为每次操作能将一个当前的单一游戏分为多个单一游戏，也就是将当前这个堆石子分为多堆石子的特殊游戏。

对于一个状态来说，不同的划分方法会产生多个不同的后继，而在一个后继中可能含有多个独立的游戏

一个后继状态的SG值即为后继状态中所有独立游戏的异或和

该状态的 SG 函数值即为后继状态的 SG 函数值中未出现过的最小值

注意区分，可以再看一遍 eg1.1 加深理解。

竞赛例题选讲

Problem A Nim or not Nim？（HDU - 3032）

题意：给定 n 堆石子，两人轮流操作，每次选一堆石子，取任意石子或则将石子分成两个更小的堆（非0），取得最后一个石子的为胜。

Solution

Mul-Nim 游戏的模板题。

我们打表找规律可以得到上面给出的性质：

$SG(x)=\left\{\begin{matrix} x-1 (x mod 4 = 0) \\ x (x mod 4= 1 or 2) \\ x+1 (x mod 4 = 3 ) \end{matrix}\right.$

Da Biao Code

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
#include <algorithm>

using namespace std;

typedef long long ll;
const int N = 50007, M = 507;
const int INF = 0x3f3f3f3f;


int sg[N];
bool vis[M + 7];
int main(){
    sg[0] = 0, sg[1] = 1;
    for (int i = 2; i < M; ++ i){
        memset(vis, 0, sizeof(vis));
        //操作一，至少取一个
        for (int j = 1; j <= i; ++ j)
            vis[sg[i - j]] = 1;
        //操作二，分成两堆，不为空
        for (int j = 1; j < i; ++ j)
                    vis[sg[j] ^ sg[i - j]] = 1;
        int j = 0;
        while (vis[j]) j ++ ;
        sg[i] = j;
    }

    for (int i = 1; i <= M; ++ i)
        printf("sg[%d] : %d\n", i, sg[i]);
    return 0;
}

View Code

AC Code

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>

using namespace std;
typedef long long ll;
typedef int itn;
const int N = 2e6 + 7;

int n, a[N], sg[N];

int main()
{
    int t;
    scanf("%d", &t);
    while(t -- ) {
        int ans = 0;
        scanf("%d", &n);
        for(int i = 1; i <= n; ++ i)
            scanf("%d", &a[i]);
        for(int i = 1; i <= n; ++ i) {
            if(a[i] % 4 == 0) sg[i] = a[i] - 1;
            else if(a[i] % 4 == 3) sg[i] = a[i] + 1;
            else sg[i] = a[i];
            ans ^= sg[i];
        }
        if(ans == 0) puts("Bob");
        else puts("Alice");
    }
    return 0;
}

View Code

Problem C A Simple Nim （HDU-5795）

游戏中有 n 堆石子，每次行动可以选择：

取走某堆的任意数量的石子（不可不取）。

将石子拆分成三堆（三堆都不可为空）。

最后取走为胜，问先手胜还是后手。

Solution

打表找规律：

$SG(x)=\left\{\begin{matrix} x-1(x mod 8 = 0)\\ x(otherwise)\\ x+1(x mod 8=7) \end{matrix}\right.$

Da Biao Code

将上题代码略作修改即可。

//操作二，分成三堆不为空
for (int j = 1; j <= i; ++ j)
    for (int k = j; k <= i; ++ k)
        if ((j + k) < i)
            vis[sg[k] ^ sg[j] ^ sg[i - j - k]] = 1;

View Code

AC代码基本同上题，略...

Every-SG游戏（每一个可以移动的棋子都要移动）

定义 Every - SG 游戏：

给定一张无向图，上面有一些棋子，两个顶尖聪明的人在做游戏，每人每次必须将所有可以移动的棋子都进行移动，最后不能移动的人输。

Solution

题目中的要求实际是“不论前面输与否，只要最后一个棋子胜利，那么就算胜利”

这样的话，能赢得游戏必须赢

因为两个人都顶尖聪明，因此当一个人知道某一个游戏一定会输的话，它一定会尽力缩短游戏的时间，当它知道某一个游戏一定会赢得话，一定会尽力延长游戏的时间

定义Every-SG游戏

对于还没有结束的单一游戏，游戏者必须对该游戏进行一步决策；其他规则与普通SG游戏相同

Every-SG游戏与普通SG游戏最大的不同就是它多了一维：时间

对于SG值为0的点，我们需要知道最少需要多少步才能走到结束，对于SG值不为0的点，我们需要知道最多需要多少步结束

这样我们用step变量来记录这个步数

posted @ 2023-06-09 17:01 青阳buleeyes 阅读(94) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

buleeyes

退役了

博弈论