组合数学

记录一些特殊的数字

卡特兰数：

1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...

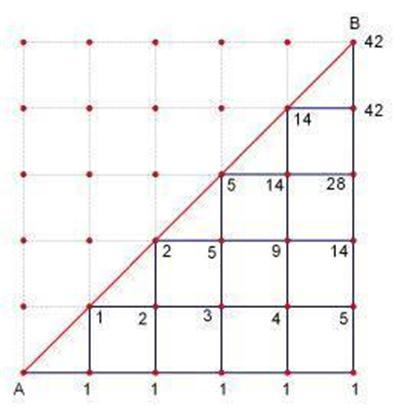
 红线就是我们的卡特兰数，递推公式： f[i][j]=f[i-1][j-1]+f[i-1][j]

即 C(2n,n)-C(2n,n-1)

eg:有 2*n 个由 '(' 和 ')' 组成的字符串，合法的括号序列是多少。

prove：从 2*n 个位置中选择 n 个作为1有 C(2*n,n)种情况。对于不合法的情况，假设第一次 1 多于 0 的位置是 2*m+1， 那么 [2*m+2,2*n] 中 0 比 1 多一个，假如将该区间中的 1->0,0->1 ，那么一共含有 n+1 个1，n-1 个0。那么所有翻转后满足该情况的数量为 C(2*n,n-1)。

 

斯特林数

第一类Stirling数

定义：将 n 个不同元素构成 m 个圆排列的数目。又根据正负性分为无符号第一类Stirling数 和带符号第一类Stirling数。有无符号Stirling数分别表现为其升阶函数和降阶函数的各项系数（类似于二项式系数），形式如下：

                                 

                                 

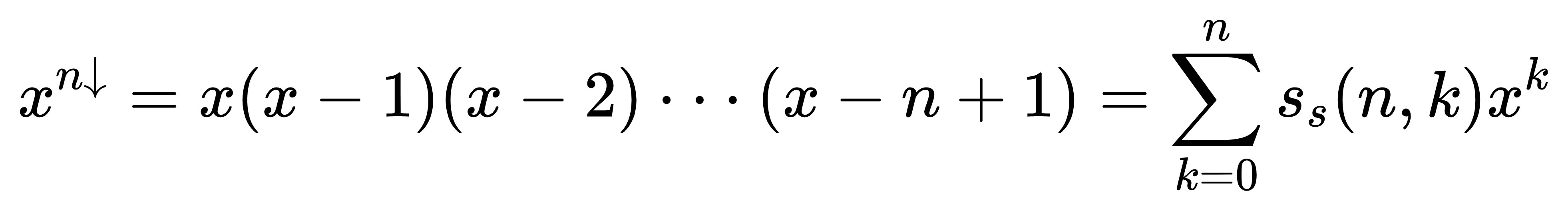
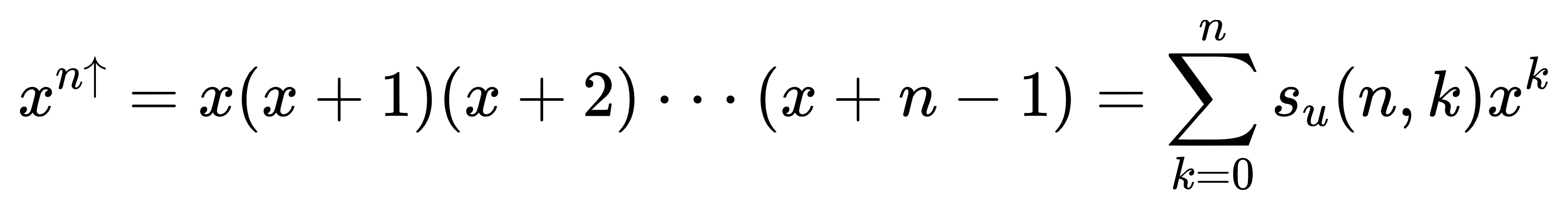
 对于有无符号Stirling数之间的关系有 s_s(n,m)=(-1)^n+ms_u(n,m)。组合数学中的Stirling数一般指第一类Stirling数。即 n 个不同元素构成 m 个圆排列的方案数。

递推式

（1）如果 n 个元素构成了 m-1 个圆排列，那么第 n+1 个元素独自构成一个圆排列。

（2）如果 n 个元素构成了 m 个圆排列，那么第 n+1 个元素可以插入到任意元素的左边。

综合两者情况，得：

　　s_u(n+1,m)=s_u(n,m-1)+n*s_u(n,m)

 

 

第二类Stirling数

定义：将 n 个不同的元素拆分成 m 的集合的方案数。

第二类Stirling数要求盒子是无区别的，所以可以得到其方案数公式：

                                     

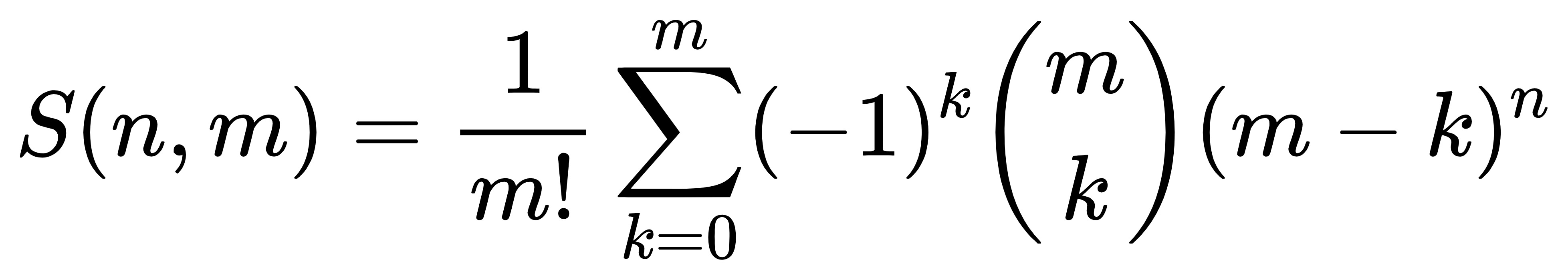
 递推式

（1）如果 n 个元素构成了 m-1 个集合，那么第 n+1 个元素单独构成一个集合。

（2）如果 n 个元素构成了 m 个集合，那么第 n+1 个元素可以插入任意一个集合。

综合两者情况，得：

　　S(n+1,m)=S(n,m-1)+m*S(n,m)

拓展

（1）n 个不同的球，放入 m 个无区别的盒子，不允许盒子为空

方案数：S(n,m)。与第二类Stirling数的定义一致。

（2）n 个不同的球，放入 m 个有区别的盒子，不允许盒子为空

方案数：m!*S(n,m)。因盒子有区别，乘上盒子的排列即可。

（3）n 个不同的球，放入 m 个无区别的盒子，允许盒子为空

方案数：。枚举非空盒的数目即可。

 （4）n 个不同的球，放入 m 个有区别的盒子，允许盒子为空

方案数：mⁿ。既然允许盒子为空，且盒子间有区别，那么对于每个球有 m 种选择，每个球相互独立。

 

 

两类Stirling数之间的关系

两类Stirling数之间的递推式和实际含义很类似，事实上他们之间存在一个互为转置的转化关系：

                        

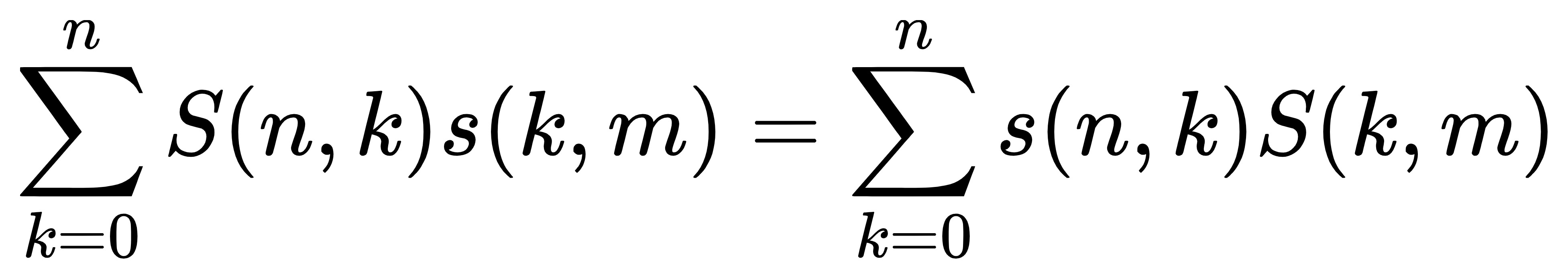
 类似于矩阵的对称转置关系。

 

斐波那契数

1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,75025,121393,196418,317811,514229,832040,1346269,2178309,3524578,5702887,9227465,14930352,24157817,39088169,63245986,102334155,165580141,267914296,433494437,701408733,1134903170,1836311903,2971215073,4807526976,7778742049,12586269025,20365011074,32951280099

递推式

f[n]=f[n-1]+f[n-2]

通项公式

 （证明过程省略...）

斐波那契与黄金分割

　　早在古希腊，就有人发现了黄金分割，似乎在1.618这个比例是最美的，建筑物的比例，雕塑的比例，然后再到美女的比例，都在这个值的区间内。这也就解释美女为什么看上去都差不多的原因。实际上，黄金分割和斐波那契数列本质上是一种概念的两种外在形式。下图是七位数的斐波那契数列，我们让相邻的两个分别相除，则会发现，数字越大，这个值越接近黄金分割值。

　　下面通过简单数学公式，证明斐波那契数列和黄金分割之间的内在关联。在极限的情况下，我们认为相邻两个元素的商等于黄金分割值，我们假设值为△，则有如下等式： 

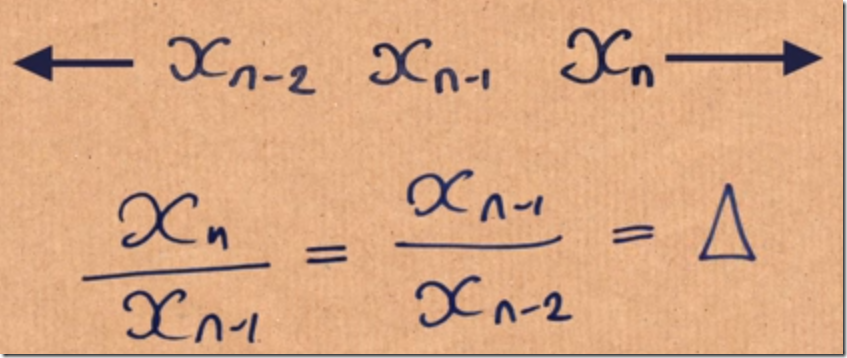
 而该数列又满足 X(n)=X(n-1)+X(n-2)，我们替换X(n)后，等式转换为：

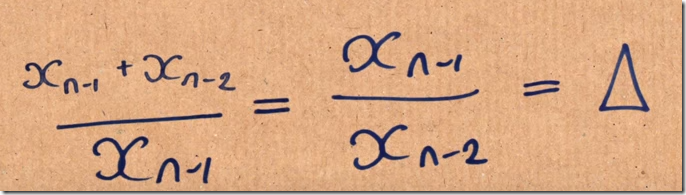
 套用二次方程公式，我们可以得到△ =(1 + √5)/2，约等于1.618。

 　　其实，这不是斐波那契数列的全部，数学家并不甘于到此为止，而是进一步的发现了更本质的规律，只要数列满足X(n) = X(n-1) + X(n-2)，无论前两个值是多少，都满足黄金分割的条件，这就是Brady Number。而斐波那契数列是最简单的特例：前两个元素均为1

       再后来，数学家还发现了费马大定理和这个数列的关系(费马大定理的证明历时三百五十年)，并应用到诸多领域（比如加密）。你会发现，学习数学并不只是为了考试，而在于让你拥有一双纯粹的，永恒的眼睛，让你看到看不见的美。