Splay（权值）

首先介绍一下BST，它的中文名字叫二叉查找树，是一切平衡树的开始。

BST

 

什么是二叉查找树呢？很显然最起码它是一棵树。但是这棵树满足一个性质：一个节点的左儿子一定比他小，右儿子一定比他大。

比如说

 

 

 

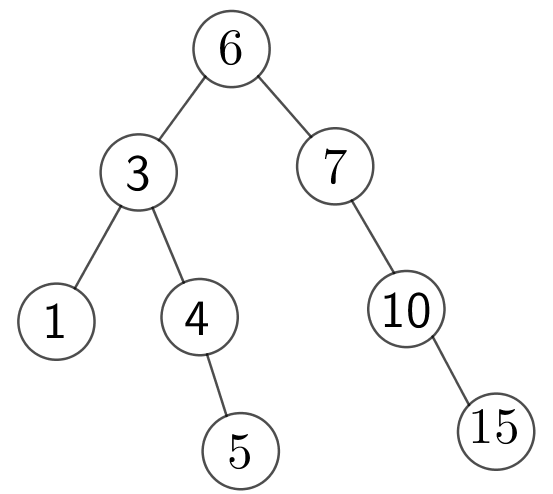
对于每次插入，它的期望复杂度是logn级别的，但是存在极端情况，面对999999......1这种情况，会直接被卡成n²

在这种情况下，平衡树出现了。

Splay

百度百科的定义：伸展树（Splay Tree），也叫分裂树，是一种二叉排序树，它能在O(log n)内完成插入、查找和删除操作。

Splay是平衡树的一种，中文名为伸展树，由丹尼尔·斯立特Daniel Sleator和罗伯特·恩卓·塔扬Robert Endre Tarjan在1985年发明的。

它的主要思想是：对于查找频率较高的点，使其处于离根节点相对较近的节点。

这样就可以保证了查找的效率。

如何定义查找效率高的点？

我们姑且认为每次被查询的点频率较高，将每次被查询的点搬到根节点去。

当然，你也可以每次查找之后随机一个点作为根，于是Treaplay这种数据结构就诞生啦

Splay基本操作

rotate

首先考虑一下，我们要把一个点挪到根，那我们首先要知道怎么让一个点挪到它的父节点。

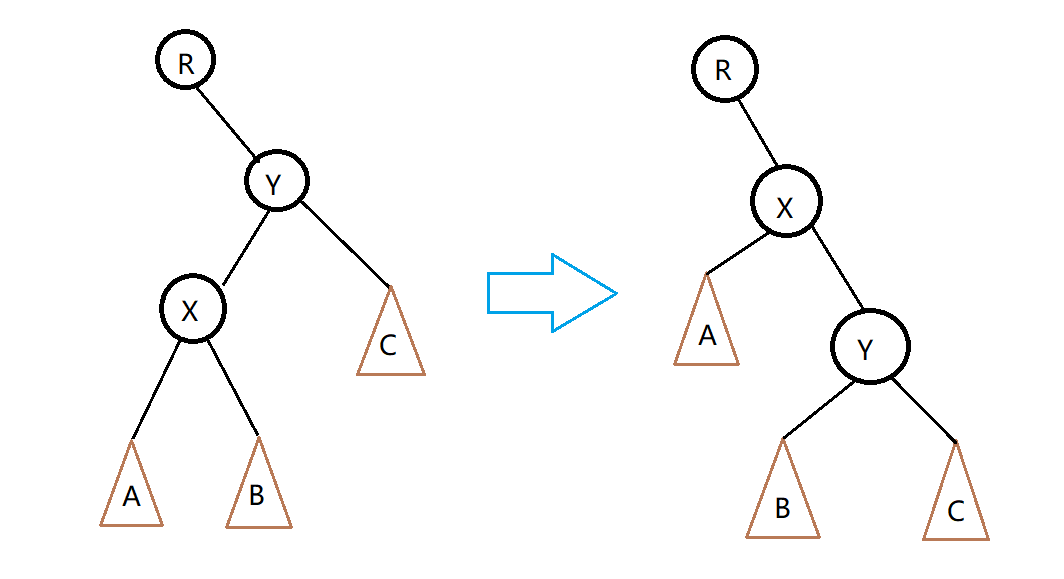
情况一

当X是Y的左儿子

这时候如果我们让X成为Y的父亲，只会影响到3个点的关系

B与X，X与Y，X与R

根据二叉排序树的性质

B会成为Y的左儿子

Y会成为X的右儿子

X会成为R的儿子，具体会成为什么儿子，这个要看Y是R的啥儿子

经过变换之后，大概是这样

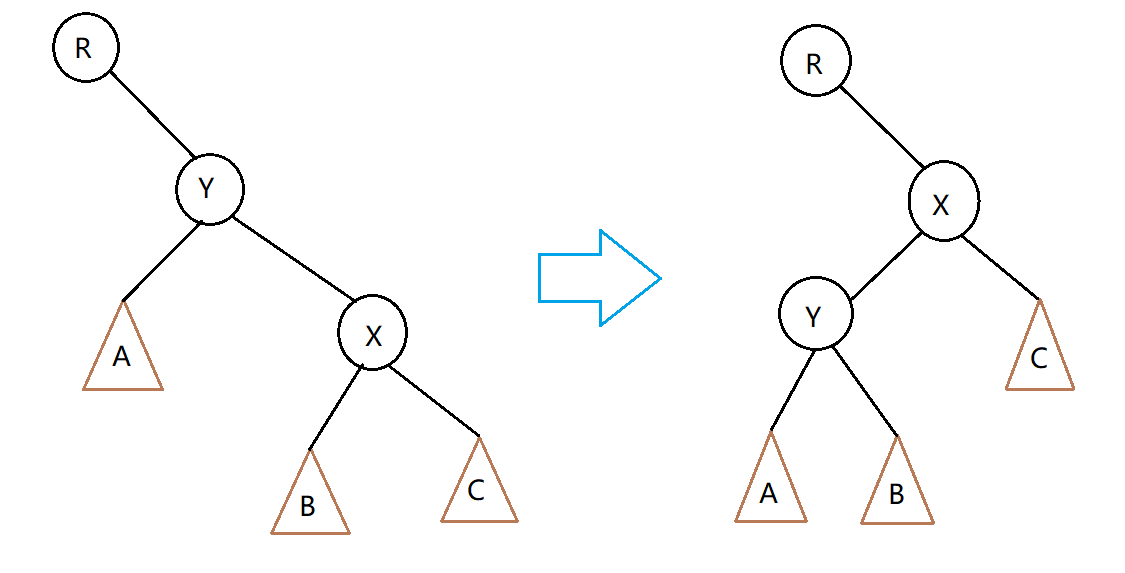
情况2

当X是Y的右儿子

本质和上面是一样的

 

 

 这两种代码单独实现都比较简单

 

void update(int x){
    t[x].size=t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}
inline void rotate(int x){
    int y=t[x].ff,z=t[y].ff,k=t[y].ch[1]==x;
    t[z].ch[t[z].ch[1]==y]=x;
    t[x].ff=z;
    t[y].ch[k]=t[x].ch[k^1];
    t[t[x].ch[k^1]].ff=y;
    t[x].ch[k^1]=y;
    t[y].ff=x;
    update(y);
}

 

Splay

Splay(x,to)是实现把x节点搬到to节点

最简单的办法，对于x这个节点，每次上旋直到to

这样会卡到O(n²)，为什么呢？我们先往下看。

Splay操作规定：每访问一个节点x后都要强制将其旋转到根节点。具体分为六种情况

 

 

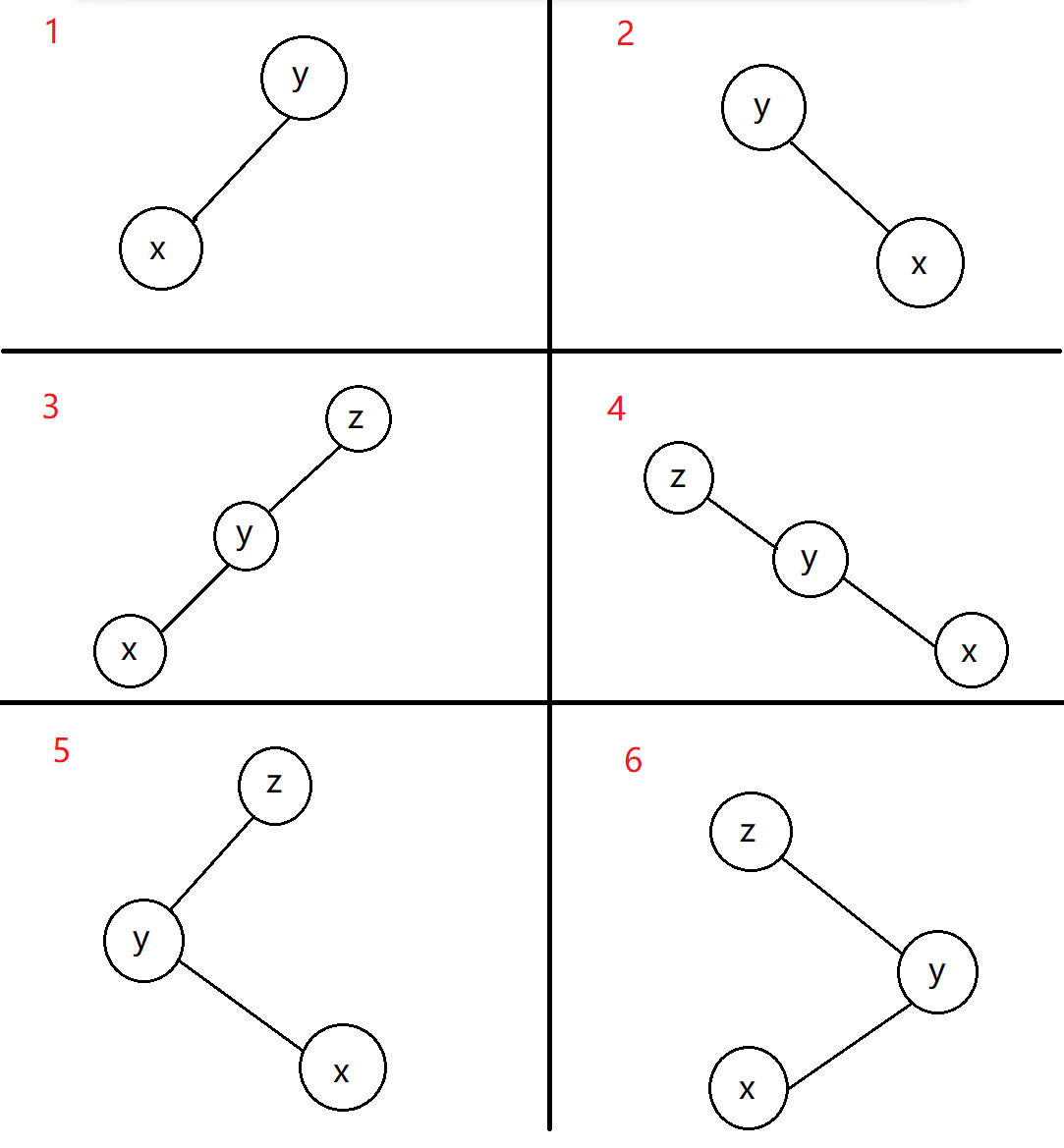
 1.zig：在y是根节点时操作。Splay树会根据x和p间的边旋转。zig存在是用于处理奇偶校验问题，仅当x在splay操作开始时具有奇数深度时作为splay操作的最后一步执行。  

　　直接将x左旋或者右旋(图1,2)

2.zig-zig：在y不是根节点且x和y都是右侧子节点或都是左侧子节点时操作。splay树首先旋转y到其父节点z，再旋转x到其父节点y。

　　即首先将y左旋或者右旋，然后将x右旋或者左旋(图3,4)

3.zig-zag：在y不是根节点且x和y一个是右侧子节点一个是左侧子节点时操作。splay首先按y和x之间的边旋转，然后按x和z新生成的结果边旋转。

　　即将x先左旋后右旋，或先右旋再左旋(图5,6)。

 

int get(int x){
    int y=t[x].ff;
    return t[y].ch[0]==x?1:0;
}
void splay(int x,int goal){
    for(int y=t[x].ff;y=t[x].ff,y!=goal;rotate(x))
        if(t[y].ff!=goal) rotate(get(x)==get(y)?y:x);
    if(goal==0) root=x;
　　 update(x);
}

 

 

请读者尝试自行模拟6种旋转情况，以理解splay的基本思想。

 

Splay的时间复杂度

因为zig和zag是对称操作，我们只需对zig，zig-zig，zing-zag操作分析复杂度。采用 势能分析(亲爱的物理)，定义一个n个节点的splay树进行了m次splay步骤。可记，定义势能函数为，在第i次操作后势能为，则我们只需要求出初始势能和每次势能变化量的和即可。

1.zig：势能的变化量为

　　　　 　　　　　　    1+w'(x)+w'(y)-w(x)-w(y)≤1+w'(y)-w(x)

　　　　　 　　　　　　　　　　　　　　　 　　　　≤1+w'(x)-w(x)

2.zig-zig：势能变化量为

　　　　　 1+w'(x)+w'(y)+w'(z)-w(x)-w(y)-w(z)≤1+w'(y)-w'(z)-w(x)-w(y)

　　　　　　　　　　　　　　　　　　　　  　　　　≤1+w'(x)-w'(z)-2w(x)

　　　　　　　　　　　　　　　　　　　　  　　　　≤3(w'(x)-w(x))

3.zig-zag：势能变化量为

　　　　　 1+w'(x)+w'(y)+w'(z)-w(x)-w(y)-w(z)≤1+w'(y)+w'(z)-w(x)-w(y)

　　　　　　　　　　　　　　　　　　　　  　　　　≤1+w'(y)+w'(z)-2w(x)

　　　　　　　　　　　　　　　　　　　　  　　　　≤2w'(x)-w'(y)-w'(z)+w'(y)+w'(z)-w(x)-w(y)

　　　　　　　　　　　　　　　　　　　　  　　　　≤2(w'(x)-w(x))

由此可见，三种splay步骤的势能全部可以缩放为 ≤3(w'(x)-w(x)).令w⁽ⁿ⁾(x)=w^(n-1)(x).令    w⁽⁰⁾(x)=w(x)，假设splay操作一次依次访问了x₁,x₂,···,x_n，最终x₁成为根节点，我们可以得到：

       　　

 

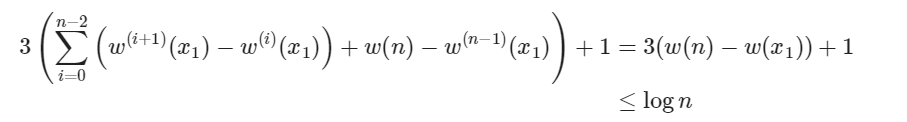
 继而可得：

    

 

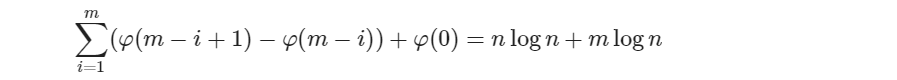
 因此，对于n个节点的splay树，做一次spaly操作的均摊复杂度为O(logn)。因此，基于splay的插入，查询，删除等操作的均摊时间复杂度也为O(logn)。

 所谓势能分析是均摊复杂度的一种分析，我认为没有触及本质，我们可以手动模拟单旋与双旋，得出两者的区别：

　　前者容易构成链，后者容易构成树

find操作 

inline void find(int x){//求出x的排名
    int u=root;
    if(!u) return;
    while(t[u].ch[x>t[u].val]&&x!=t[u].val)
        u=t[u].ch[x>t[u].val];
    splay(u,0);
}

 

insert操作

inline void insert(int x){//插入x
    int u=root,ff=0;
    while(u&&t[u].val!=x){
        ff=u;
        u=t[u].ch[x>t[u].val];
    }
    if(u) t[u].cnt++;
    else{
        u=++tot;
        if(ff) t[ff].ch[x>t[ff].val]=u;
        t[u].ch[0]=t[u].ch[1]=0;
        t[tot].ff=ff;t[tot].val=x;
        t[tot].cnt=1;t[tot].size=1;
    }
    splay(u,0);
}

 

前驱/后继操作Next

inline int Next(int x,int f){
    find(x);
    int u=root;
    if(t[u].val>x&&f) return u;
    if(t[u].val<x&&!f) return u;
    u=t[u].ch[f];
    while(t[u].ch[f^1]) u=t[u].ch[f^1];
　　 splay(u,0);
    return u;
}

 

删除操作

inline void Delete(int x){
    int last=Next(x,0);
    int next=Next(x,1);
    splay(last,0);splay(next,last);
    int del=t[next].ch[0];
    if(t[del].cnt>1)
        t[del].cnt--,splay(del,0);
    else t[next].ch[0]=0,splay(next,0);
}

 

第K大

 

inline int kth(int x){
    int u=root;
    if(t[u].size<x) return 0;
    while(1){
        int y=t[u].ch[0];
        if(x>t[y].size+t[u].cnt){
            x-=t[y].size+t[u].cnt;
            u=t[u].ch[1];
        }
        else{
            if(t[y].size>=x) u=y;
            else return splay(u,0),t[u].val;
        }
    }
}

 

代码

 

#include<bits/stdc++.h>
#define ls(p) p<<1
#define rs(p) p<<1|1
using namespace std;
const int N=3e6+10;
struct splay_tree{
    int ff,cnt,ch[2],val,size;
}t[N];
int root,tot,n,q;
int get(int x){
    int y=t[x].ff;
    return t[y].ch[0]==x?1:0;
}
void update(int x){
    t[x].size=t[t[x].ch[0]].size+t[t[x].ch[1]].size+t[x].cnt;
}
inline void rotate(int x){
    int y=t[x].ff,z=t[y].ff,k=t[y].ch[1]==x;
    t[z].ch[(t[z].ch[1]==y)]=x;
    t[x].ff=z;
    t[y].ch[k]=t[x].ch[k^1];
    t[t[x].ch[k^1]].ff=y;
    t[x].ch[k^1]=y;
    t[y].ff=x;
    update(y);
}
void splay(int x,int goal){
    for(int y=t[x].ff;y=t[x].ff,y!=goal;rotate(x))
        if(t[y].ff!=goal) rotate(get(x)==get(y)?y:x);
    if(goal==0) root=x;
    update(x);
}
inline void find(int x){
    int u=root;
    if(!u) return;
    while(t[u].ch[x>t[u].val]&&x!=t[u].val)
        u=t[u].ch[x>t[u].val];
    splay(u,0);
}
inline void insert(int x){
    int u=root,ff=0;
    while(u&&t[u].val!=x){
        ff=u;
        u=t[u].ch[x>t[u].val];
    }
    if(u) t[u].cnt++,t[u].size++;
    else{
        u=++tot;
        if(ff) t[ff].ch[x>t[ff].val]=u;
        t[u].ch[0]=t[u].ch[1]=0;
        t[tot].ff=ff;t[tot].val=x;
        t[tot].cnt=1;t[tot].size=1;
    }
    splay(u,0);
}
inline int Next(int x,int f){
    find(x);
    int u=root;
    if(t[u].val>x&&f) return u;
    if(t[u].val<x&&!f) return u;
    u=t[u].ch[f];
    while(t[u].ch[f^1]) u=t[u].ch[f^1];
    splay(u,0);
    return u;
}
inline void Delete(int x){
    int last=Next(x,0);
    int next=Next(x,1);
    splay(last,0);splay(next,last);
    int del=t[next].ch[0];
    if(t[del].cnt>1)
        t[del].cnt--,t[del].size--,splay(del,0);
    else t[next].ch[0]=0,splay(next,0);
}
inline int kth(int x){
    int u=root;
    if(t[u].size<x) return 0;
    while(1){
        int y=t[u].ch[0];
        if(x>t[y].size+t[u].cnt){
            x-=t[y].size+t[u].cnt;
            u=t[u].ch[1];
        }
        else{
            if(t[y].size>=x) u=y;
            else return splay(u,0),t[u].val;
        }
    }
}
int main(){
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin>>q;
    insert(1e9),insert(-1e9);
    while(q--){
        int op,x;
        cin>>op>>x;
        if(op==1){
            insert(x);
        }
        else if(op==2){
            Delete(x);
        }
        else if(op==3){
            find(x);
            cout<<t[t[root].ch[0]].size<<'\n';
        }
        else if(op==4){
            cout<<kth(x+1)<<'\n';
        }
        else if(op==5){
            cout<<t[Next(x,0)].val<<'\n';
        }
        else  cout<<t[Next(x,1)].val<<'\n';
    }

    return 0;
}