【剑指Offer】1、二维数组中的查找

【剑指Offer】1、二维数组中的查找

题目描述：

在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

解题思路：

很明显，由于该二维数组上到下递增，左到右递增的特殊性，遍历整个矩阵进行查找不是该题目的意图所在。总结规律我们可以发现：应该从矩阵的右上角或者左下角开始查找。

以右上角为例，首先选取右上角的数字，如果该数字等于要查找的数字，则查找过程结束；如果该数字大于要查找的数字，则说明该列其他元素都大于要查找的数字，便可以删掉该列；如果该数字小于要查找的数字，则说明该行其他元素也都小于要查找的数字，便可以删掉该行。

这样，每一次比较都可以剔除一行或者一列，进而缩小查找范围，时间复杂度为O(n)。

举例：

比如在下面的二维数组中查找数字7，查找过程如下：

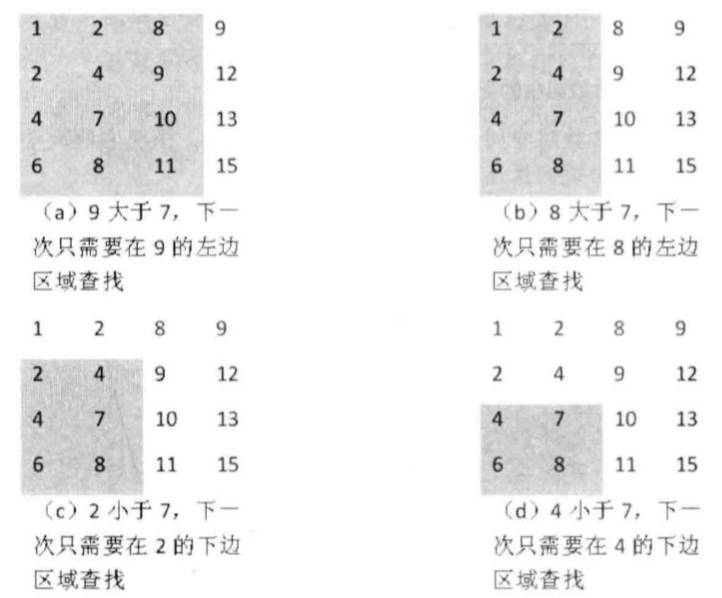
编程实现（Java）：

public class Solution {
    public boolean Find(int target, int [][] array) {
        /*
        思路：从左下角（或者右上角）开始查找，因为该行右边大于它，上边小于它，每次比较可以删除某一行或者某一列
        注意：左上和右下不可以，因为无法减小问题规模（行和列都无法删除）
        */
        if(array==null)
            return false;
        int row=array.length; //行数
        int col=array[0].length; //列数
        for(int i=row-1,j=0;i>=0&&j<col;){ //从左下角开始查找
            if(array[i][j]==target) //找到
                return true;
            else if(array[i][j]>target) //不可能在该行，跳过该行
                i--;
            else //不可能在该列，跳过该列
                j++;
        }
        return false;
    }
}