AcWing：175. 电路维修（bfs）

达达是来自异世界的魔女，她在漫无目的地四处漂流的时候，遇到了善良的少女翰翰，从而被收留在地球上。

翰翰的家里有一辆飞行车。

有一天飞行车的电路板突然出现了故障，导致无法启动。

电路板的整体结构是一个R行C列的网格（R,C≤500），如下图所示。

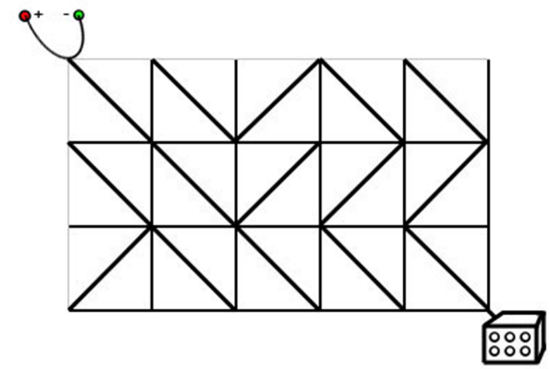
每个格点都是电线的接点，每个格子都包含一个电子元件。

电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。

在旋转之后，它就可以连接另一条对角线的两个接点。

电路板左上角的接点接入直流电源，右下角的接点接入飞行车的发动装置。

达达发现因为某些元件的方向不小心发生了改变，电路板可能处于断路的状态。

她准备通过计算，旋转最少数量的元件，使电源与发动装置通过若干条短缆相连。

不过，电路的规模实在是太大了，达达并不擅长编程，希望你能够帮她解决这个问题。

输入格式

输入文件包含多组测试数据。

第一行包含一个整数T，表示测试数据的数目。

对于每组测试数据，第一行包含正整数R和C，表示电路板的行数和列数。

之后R行，每行C个字符，字符是"/"和"\"中的一个，表示标准件的方向。

输出格式

对于每组测试数据，在单独的一行输出一个正整数，表示所需的缩小旋转次数。

如果无论怎样都不能使得电源和发动机之间连通，输出NO SOLUTION。

数据范围

1≤R,C≤5001≤R,C≤500,
1≤T≤51≤T≤5

输入样例：

1
3 5
\\/\\
\\///
/\\\\

输出样例：

1

样例解释

样例的输入对应于题目描述中的情况。

只需要按照下面的方式旋转标准件，就可以使得电源和发动机之间连通。

 

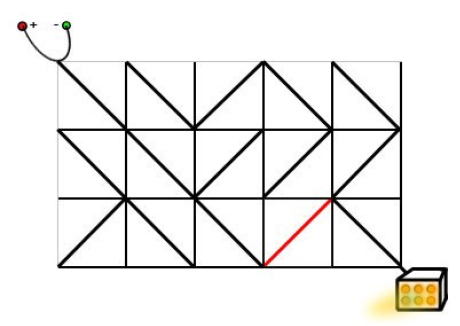
算法：bfs

题意：从原点到最后的那个端点需要的最短距离，如果当前移动的时候有适当的电线的话，你的移动的距离就是0，否则你就需要旋转一下，移动的距离就是1。注：你只能斜着走。

题解：你只需要满足单调性，每条路径都走一次，取最小值就行，因为只有0或者1，所以用双端队列求解即可。

#include <iostream>
#include <cstdio>
#include <deque>
#include <memory.h>

using namespace std;

#define INF 0x3f3f3f3f
const int maxn = 5e2+7;

char Map[maxn][maxn];
int dir1[4][2] = {-1, -1, 1, 1, 1, -1, -1, 1};  //方向数组，点移动的数组
int dir2[4][2] = {0, 0, 1, 1, 1, 0, 0, 1};      //这个是控制每个电线的数组
int dis[maxn][maxn];    //存储着原点到当前位置的最小距离
int n, m;

bool check(int x, int y) {
    if(x < 0 || x > n || y < 0 || y > m) {
        return false;
    }
    return true;
}

void bfs() {
    deque<pair<int, int > > q;
    memset(dis, INF, sizeof dis);
    dis[0][0] = 0;
    q.push_back(make_pair(0, 0));
    while(!q.empty()) {
        pair<int, int> t = q.front();
        q.pop_front();
        for(int i = 0; i < 4; i++) {
            int dx = t.first + dir1[i][0], dy = t.second + dir1[i][1];
            int tx = t.first + dir2[i][0], ty = t.second + dir2[i][1];
            int tmp = Map[tx][ty] != (i <= 1 ? '\\' : '/');     //如果现在我要移动的位置有适当的电线，就是1，否是是0
            if(check(dx, dy) && (dis[dx][dy] > dis[t.first][t.second] + tmp)) { 
                dis[dx][dy] = dis[t.first][t.second] + tmp;
                if(tmp) {   
                    q.push_back(make_pair(dx, dy));     
                } else {
                    q.push_front(make_pair(dx, dy));
                }
            }
        }
    }
}

int main() {
    int T;
    scanf("%d", &T);
    while(T--) {
        scanf("%d %d", &n, &m);
        for(int i = 1; i <= n; i++) {
            getchar();
            for(int j = 1; j <= m; j++) {
                scanf("%c", &Map[i][j]);
            }
        }
        bfs();
        // for(int i = 0; i <= n; i++) {
        //     for(int j = 0; j <= m; j++) {
        //         printf("%12d ", dis[i][j]);
        //     }
        //     printf("\n");
        // }
        if(dis[n][m] < INF) {
            printf("%d\n", dis[n][m]);
        } else {
            printf("NO SOLUTION\n");
        }
    }
    return 0;
}