参考地址：
贪心学院:https://github.com/GreedyAIAcademy/Machine-Learning
1 回顾一下决策树
学习XGBoost过程中险些把之前决策数的知识也弄迷茫了,因此首先回顾一下决策树
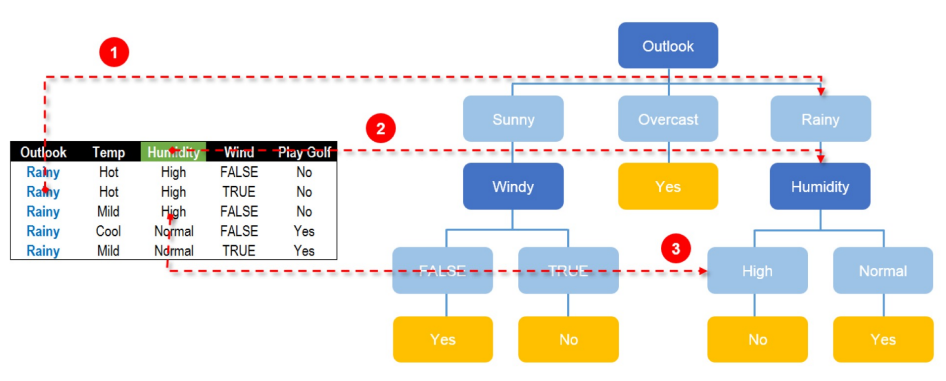
据信息熵来的,也就是信息熵大的字段会更靠近决策树的根节点
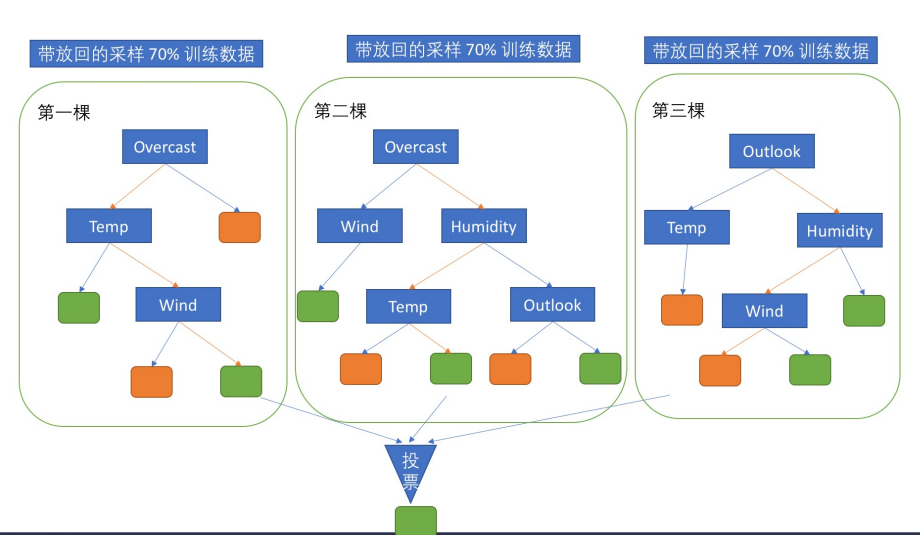
林最重要的就是根据不同的字段的先后决策顺序组成不同的树。
2 XGBoost举例
说实话刚接触XGBoost算法的时候我就蒙了,仔细分析了例子之后就清晰了
2.1 问题和结果
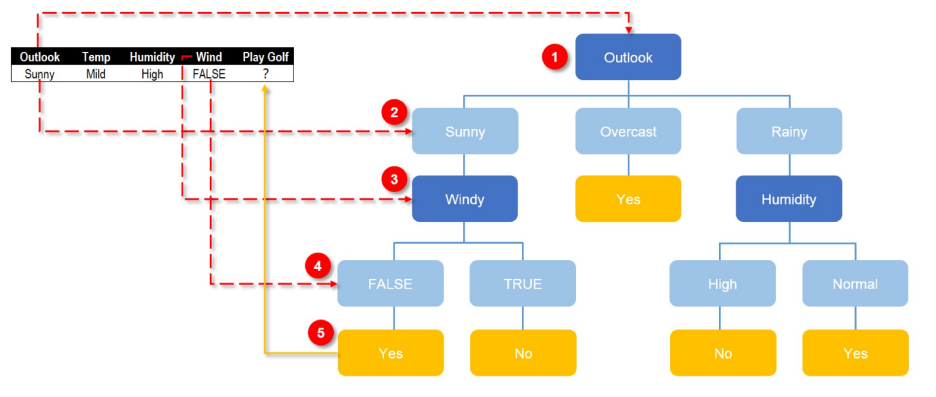
请分析下图示例：
假设我们不知道用户年龄的情况下,通过用户行为来预测用户的年龄
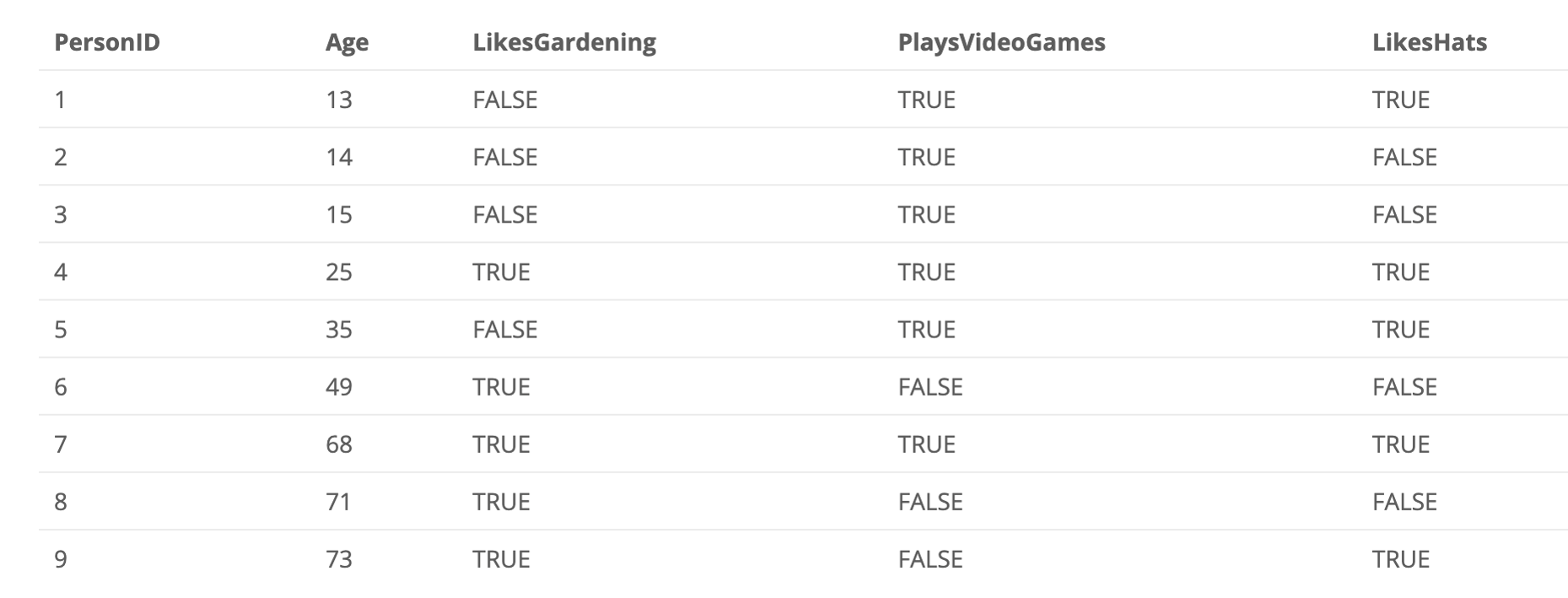
,XGBoost的计算结果如下：
2.2 第一棵树的计算方法
19.25和57.2是怎么来的呢？
$ (13 + 14 + 15 + 35) / 4 = 19.25 \(
\) (25 + 49 + 68 + 71 + 73) / 5 = 57.2$
为什么要这么算？因为XGBoost算法就是一个号称"三个臭皮匠,顶个诸葛亮"的算法,其强悍之处在于多棵树计算结果的迭代,所以最初取平均值影响不大。
这里面还有一个残差(residual)的概念,残差 = 实际结果 - 预测结果
比如：Person1的Tree1残差为\(13 - 19.25 = -6.25\)
2.3 第二棵树的计算方法
(https://img2018.cnblogs.com/blog/753880/201908/753880-20190802183318845-666594384.png)
这里要注意是第二棵决策树,并非是第一棵树的一个节点。
第一棵决策树是按LikeGardening来分的,第二棵树是按PlaysVedioGames来分的。
第二棵树的预测结果是怎么算的？
$ 7.133 = (-8.2 + 13.8 + 15.8) / 3 \(
\) -3.567 = (-6.25 -5.25 -4.25 -32.2 + 15.75 + 10.08) / 6 \(
也就是第二棵树的预测结果是第一棵树残差的平均数。
最终的联合预测结果的计算方法：
比如：Person1的计算方法：
\) 15.683 = 19.25 + (-3.567) \(
最新的残差的算法：
\) 2.683 = 15.683 - 13 $
从上面的例子中我们可以看出,实际上问题是由预测年龄转变成了找到最佳的残差值。
这样多棵树就起到了联合学习的效果，残差也会逐渐逼近最终的真实年龄值。
这样做的好处就在于节省了很大的计算量，也因此XGBoost会火。
Bagging：Leverages unstable base learners that are weak because of overfitting
Boosting: Leverage stable base learners that are weak because of underfitting
3 XGBoost公式推导
3.1 第一种理解公式
残差：
\(y_{i,residual} = y_{i,true}-y_{i,predict}\)
预测值：
$ y_{(i,k,predict)} = \frac{1}{m}\sum_{j}^{m} y_{(i,j,k-1)} , y_{(i,0,predict)}=y_{(i,true)} $
其中m就是i所在叶子节点所包含的记录数, 我们求和的就是此叶子节点中每条记录的上一个棵树的预测值。
最终的结果就是把所有的预测值加起来就行了。
3.2 第二种理解公式
这样标达过于麻烦,因此我们换一种简单的方法：
假设训练了K棵树,\(f_{k}(x_{i})\)为第i个人在第k棵树上的预测值(其实这个值就是上面例子中的残差而已),而训练完k棵树的最终预测值是：
\hat{y}{i} = \sum^{K}f_{k}(x_{i})
有预测值并不是我们的目标，我们的目标是方差最小，因此目标函数为：
第2节的例子，后面的公式推导就是按部就班地代入就行了。
首先将目标函数展开，再封装用泰勒公式模型求导，找出极值点再带回到目标函数求得极值的值，把k个极值加起来作为得分就可以找到最佳的树的分割了。
(后面的部分太麻烦了,就不一一解释了)
