BUGAWAY算法小抄-差分数组

BUGAWAY算法小抄-差分数组

什么是差分数组？

差分数组的思想是通过对原始数组进行处理，得到一个新的数组（差分数组），利用该数组来高效地进行区间更新操作。具体来说，差分数组记录的是相邻元素之间的差值，而不是原始数组的元素本身。

差分数组的原理

1. 差分数组的构造：

假设有一个数组 A = [a1, a2, a3, ..., an]，我们可以构造一个差分数组 D，使得 D[i] = A[i] - A[i-1]（D[0] = A[0]）。

这样，D 记录了 A 中相邻元素的差值。

2. 区间更新：

在差分数组中，给定一个区间 [l, r]，想要将该区间内的所有元素加上某个值 v，只需要做以下两步操作：

• D[l] += v，表示从位置 l 开始所有元素都增加 v。
• D[r+1] -= v，表示从位置 r+1 开始所有元素都不再增加 v。

最后，通过差分数组计算得到原始数组的最终值。

3. 恢复原始数组：

利用差分数组 D 可以恢复原始数组 A，通过累加差分数组的元素得到原数组的值：

• A[0] = D[0]
• A[i] = D[i] + D[i-1] + ... + D[0] （即累加差分数组的值）

差分数组的算法应用

差分数组主要用于高效地处理区间更新操作，通常出现在以下几类问题中：

1. 区间加法操作：

如果需要对数组的一个区间 [l, r] 进行加法更新，传统的方法可能需要遍历区间内的每个元素，时间复杂度是 O(r - l + 1)，但通过差分数组可以将区间更新的时间复杂度降为 O(1)。这使得对于大量的区间更新操作，算法效率大大提高。

示例：

• 给定一个数组 arr 和多个区间 [l, r, v]，对于每个区间，将 arr[l] 到 arr[r] 之间的所有元素加上 v。使用差分数组处理，可以将时间复杂度从 O(k * n)（k 个区间，n 为数组大小）降低到 O(k + n)。

2. 区间查询问题：

如果题目需要在处理区间更新的同时进行区间查询，差分数组也可以与前缀和结合，帮助实现高效的查询和更新。

• 差分数组用于快速实现区间加法更新。

• 前缀和则用于在差分数组上进行恢复，快速查询指定区间的和。

示例：

• 对数组进行区间更新后，要求查询某个位置的元素值。差分数组通过前缀和可以在 O(1) 时间内恢复出数组元素。

3. 区间求和与区间赋值操作：

在一些变种问题中，差分数组的思想可以用来进行区间求和或其他区间相关的操作，减少时间复杂度。

---

🥱闲话少说，直接上例题！

实践

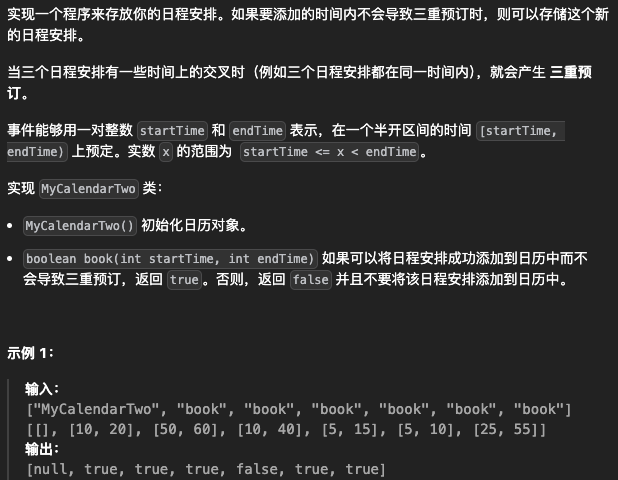
731. 我的日程安排表 II

class MyCalendarTwo {
    // 由于时间范围比较大，可以考虑用TreeMap实现
    TreeMap<Integer, Integer> cnt;

    public MyCalendarTwo() {
        cnt = new TreeMap<Integer, Integer>();
    }

    public boolean book(int start, int end) {
        // 预定[start,end]的时段，说明该时段每个时点的预定数都需要+1——符合差分数组“区间更新”的思想。
        int ans = 0;
        int maxBook = 0;
        cnt.put(start, cnt.getOrDefault(start, 0) + 1);
        cnt.put(end, cnt.getOrDefault(end, 0) - 1);
        for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
            int freq = entry.getValue();
            maxBook += freq;
            ans = Math.max(ans, maxBook);
            if (maxBook > 2) {
                // 复原操作
                cnt.put(start, cnt.getOrDefault(start, 0) - 1);
                cnt.put(end, cnt.getOrDefault(end, 0) + 1);
                return false;
            }
        }
        return true;
    }
}

/**
 * Your MyCalendarTwo object will be instantiated and called as such:
 * MyCalendarTwo obj = new MyCalendarTwo();
 * boolean param_1 = obj.book(startTime,endTime);
 */

732. 我的日程安排表 III

class MyCalendarThree {
    TreeMap<Integer, Integer> cnt;
    public MyCalendarThree() {
        cnt = new TreeMap<Integer, Integer>();
    }
    
    public int book(int start, int end) {
        int maxBook = 0;
        int ans = 1;
        cnt.put(start, cnt.getOrDefault(start, 0) + 1);
        cnt.put(end, cnt.getOrDefault(end, 0) - 1);
        for(Map.Entry<Integer, Integer> entry: cnt.entrySet()){
            int freq = entry.getValue();
            maxBook += freq;
            ans = Math.max(ans, maxBook);
        }
        return ans;
    }
}

/**
 * Your MyCalendarThree object will be instantiated and called as such:
 * MyCalendarThree obj = new MyCalendarThree();
 * int param_1 = obj.book(startTime,endTime);
 */