BUGAWAY算法小抄-树状数组(2024.03.23 更新)
什么是树状数组?
树状数组是支持单点修改和区间查询的、代码量小的数据结构。
事实上,树状数组能解决的问题是线段树(一棵二叉树,每个节点表示一个区间,并存储该区间的一些相关信息。线段树可以高效地进行区间查询和区间更新操作。不是本文重点)能解决的问题的子集:树状数组能做的,线段树一定能做;线段树能做的,树状数组不一定可以。然而,树状数组的代码要远比线段树短,时间效率常数也更小,因此仍有学习价值。
有时,在差分数组和辅助数组的帮助下,树状数组还可解决更强的区间加单点值和区间加区间和问题。
举个栗子🌰,想知道a[1,...,7]的前缀和,怎么做?
一种方法就是将所有数都加起来。但如果已知三个数 A,B,C,A=a[1,...,4],B=a[5,...,6],C=a[7,...,7]。求和只需要 A + B + C 。
这就是树状数组能快速求解信息的原因:我们总能将一段前缀拆成 不多于logn 段区间,使得这 logn 段区间的信息是 已知的。于是,我们只要合并这些段区间的信息,就可以得到答案,相比于原先直接合并 n 个元素,效率有了很大提升。
直接上结论,不难发现,c[x]管辖的一定是[x - lowbit(x)+1, x]的区间总信息。如c[88]管辖的是[88-8+1,...,88]即[81,...,88]的区域($88_{(10)}$=$1011000_{(2)}$,因此 lowbit(88) = $1000_{(2)}$=8)。
⚠️注意:lowbit 指的不是x 的最低位1 所在的位数 k,而是这个 1 和其后面的 0 所组成的 $2^k$。
lowbit 对应代码为:
public int lowbit(int x){
// x 的二进制中,最低位的 1 以及后面所有 0 组成的数。
// lowbit(0b01011000) == 0b00001000
// ~~~~^~~~
// lowbit(0b01110010) == 0b00000010
// ~~~~~~^~
return x & -x;
}
树状数组有两大核心功能:
单点更新update(i, v): 把序列 i 位置的数加上一个值 v;区间查询query(i): 查询序列 [1⋯i] 区间的区间和,即 i 位置的前缀和;
修改和查询的时间代价都是 O(logn),其中 n 为需要维护前缀和的序列的长度。
OK,我们不扯长篇大论,以练促学,接下来我们实操一下!💪
实践
【板子题】307. 区域和检索 - 数组可修改
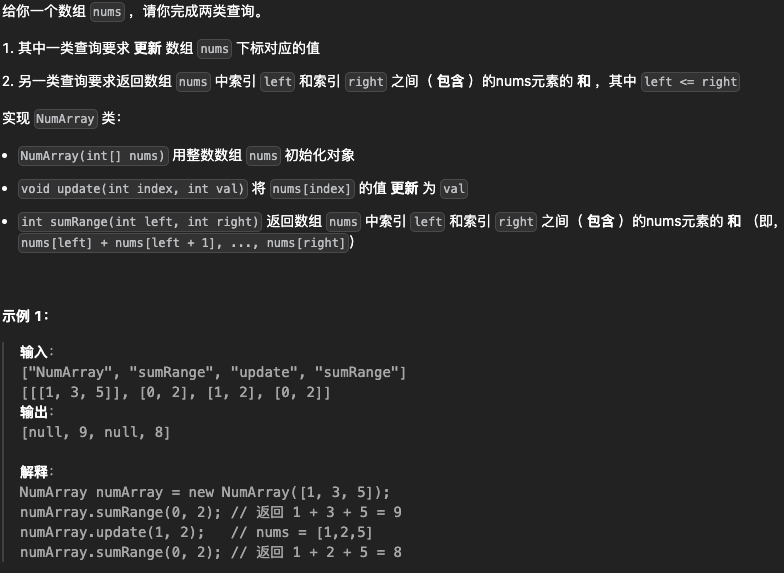
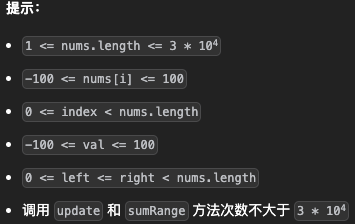
class NumArray {
private int[] nums; // 基础数组
private int[] tree; // 树状数组,功能是单点修改和区间查询。下标表示右边界。
public void add(int index, int val) {
// 单点修改,把序列第 index 个数增加 val
// 为保证效率,我们只需遍历并修改管辖了 a[index]的 tree[y],其他的 tree 没有明显变化
// 管辖 a[index]的 tree[y] 一定包含tree[index]。所以 y 在形态上是 index 的祖先
// 因此我们从 index 开始不断往上跳父亲,直到超出数组边界
while (index < tree.length) {
tree[index] += val;
index += lowbit(index);
}
}
public int prefixSum(int index) {
// 区间查询,查询前 index 个元素的前缀和
int sum = 0;
while (index > 0) {
sum += tree[index];
index -= lowbit(index);
}
return sum;
}
public NumArray(int[] nums) {
this.tree = new int[nums.length + 1];
this.nums = nums;
for (int i = 0; i < nums.length; i++) {
add(i + 1, nums[i]);
}
}
public void update(int index, int val) {
add(index + 1, val - nums[index]);
nums[index] = val;
}
public int sumRange(int left, int right) {
return prefixSum(right + 1) - prefixSum(left);
}
// lowbit 函数计算区间管辖的左边界
public int lowbit(int x) {
return x & -x;
}
}
【离散化树状数组】315. 计算右侧小于当前元素的个数
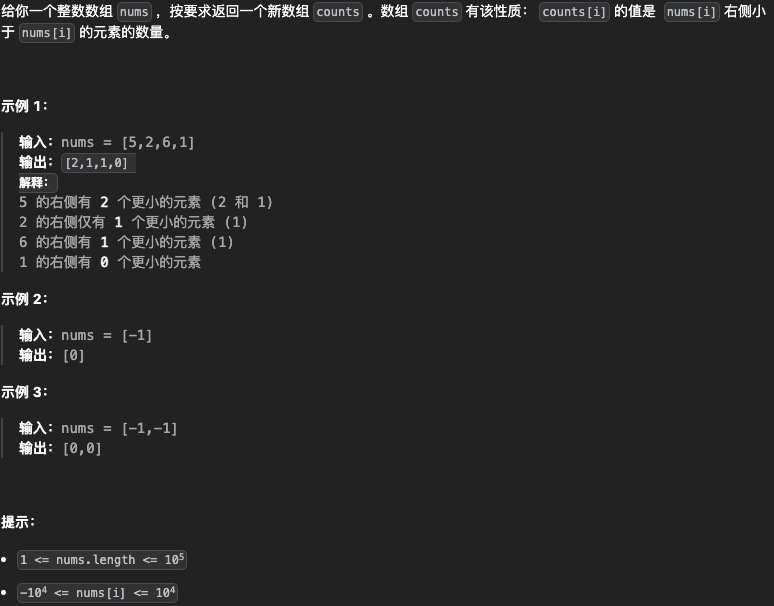
class Solution {
int[] a; // 原始数组
int[] c; // 树状数组
public List<Integer> countSmaller(int[] nums) {
// 离散化+ 树状数组
// 离散化的目的是因为“把原序列的值域映射到一个连续的整数区间,并保证它们的偏序关系不变。“
List<Integer> resultList = new ArrayList<>();
discretization(nums);
init(nums.length);
for(int i = nums.length -1; i >= 0; i--){
int id = getId(nums[i]); // 离散化之后相当于id 为 nums[i]在 nums 中第 id 小的元素
resultList.add(query(id-1)); // id-1是因为不包括 id 的个数
update(id);
}
Collections.reverse(resultList);
return resultList;
}
public void init(int length){
c = new int[length];
Arrays.fill(c,0);
}
public int lowbit(int x){
return x & -x;
}
public int query(int pos){
// 范围查询
int ret = 0;
while(pos > 0){
ret += c[pos];
pos -= lowbit(pos);
}
return ret;
}
public void update(int pos) {
// 单点更新
while( pos < c.length){
c[pos] += 1;
pos += lowbit(pos);
}
}
// 离散化操作
public void discretization(int[] nums){
Set<Integer> set = new HashSet<Integer>();
for(int num: nums){
set.add(num);
}
int size = set.size(); // 有 size 个不一样的数
a = new int[size];
int index = 0;
for(int num: set){
a[index++] = num;
}
Arrays.sort(a);
}
public int getId(int x){
return Arrays.binarySearch(a,x) + 1;
}
}
解释:

过程如下:





 浙公网安备 33010602011771号
浙公网安备 33010602011771号