leetcode解题报告 32. Longest Valid Parentheses 用stack的解法

第一道被我AC的hard题！菜鸡难免激动一下，不要鄙视..

Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.

For "(()", the longest valid parentheses substring is "()", which has length = 2.

Another example is ")()())", where the longest valid parentheses substring is "()()", which has length = 4.

题目大意：给出一个字符串，给出左右括号完全匹配的最大子串长度。

 

最开始想着套动态规划，当s[i]..s[j]是完全匹配的，dp[i][j] = j - i +1. 否则dp[i][j] = 0;

然后对各个长度判断。。太笨了。O(n2)的复杂度，超时是必然的，还有bug。

 

忍不住点开discuss，看了一眼标题，人家是O(n)复杂度，一遍过。惊叹！用的stack。我怎么这么笨呢。。括号匹配、表达式求值就用过stack啊。

懒得琢磨答案的代码，继续自己想。感觉这个题有戏。

在纸上画个字符串模拟，怎么用好一个栈(或者两个栈)。

直接写最后的想法了。中间过程全靠灵感。。

 

遇到(就压栈。

遇到)，取出一个元素。如果取出的是(，匹配了，把()变成数字2，压进去。

如果取出的是数字，继续取，把取出的所有连续数字变成一个长度，直到pop出来的不是数字(字符或者空)。

 把最近的左右括号变成2，把相邻的2变成4，把相邻的数字变成更大的和。

然后进行匹配的时候，栈里的数字当做透明的。先全部取出数字，再判断左右括号的匹配。

不管是否匹配，最后要把数字和符号原路压回去。

用字符串演示一下过程：

 

i = 0和1，左括号入栈

i = 2，s[1]出栈，匹配。变成2压入栈。

i = 3和4， s[3]、s[4]入栈

i = 5，s[4]出栈，变成2压进去。

i = 6，把2取出来，把s[3]取出来，s[3]和s[6]匹配变成2。加上取出来的2，变成4，压进去。

....

 

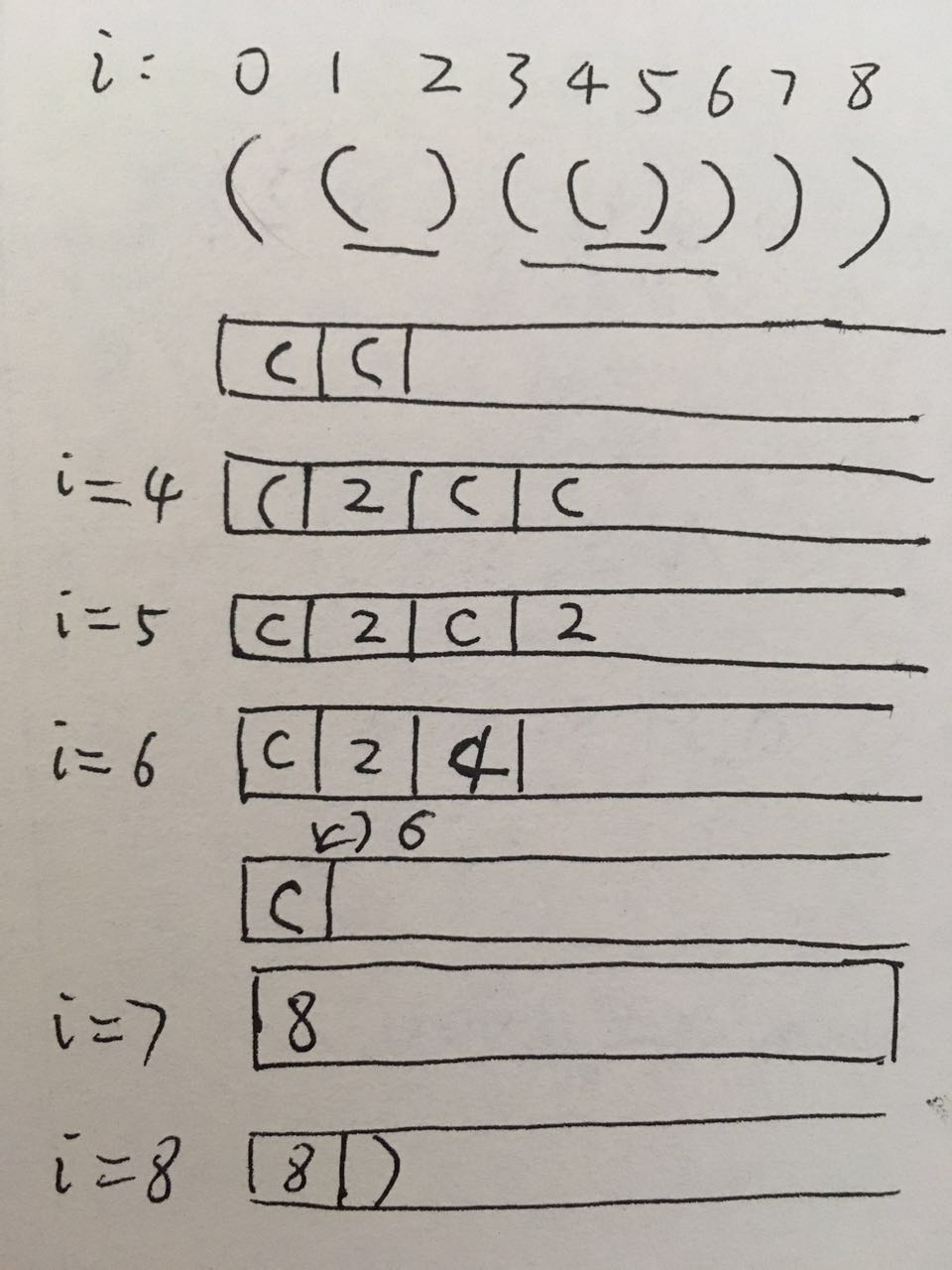
最后计算栈里面连续的、不被字符隔断的数字的总和的最大值。

 

这里遇到一个问题，就是数字 和 () 符号怎么区分。我用了负数来表示。中间出了两次bug，就是有的地方依然用char表示的，负数肯定不能用char了。。

 

上代码了。。用的C语言，自己写的栈。笨啊   赶紧把STL搞起来！

虽然代码很长，但是好像可读性强一点？ 呵呵

struct stack{
    int *data;　　　　//存放 括号或者已经匹配的个数(负值)
    int n;　　　　　　//size
    int top;
};

typedef struct stack* Stack;

Stack new_stack(int n)
{
    Stack hd = (Stack)malloc(sizeof(struct stack));
    hd->data = (int*)malloc(n*sizeof(int));
    hd->top = -1;
    hd->n = n;
    return hd;
}

void del_stack(Stack hd)
{
    if(hd)
    {
        if(hd->data) free(hd->data);
        free(hd);
    }
}
bool is_full(Stack hd)
{
    return hd->top == hd->n - 1;
}

void push(Stack hd, int ch)
{
    if( is_full(hd) )
    {
        int *tmp = (int*)malloc(sizeof(int)*(hd->n + 10));
        memcpy(tmp,hd->data,hd->n*sizeof(int));
        free(hd->data);
        hd->data = tmp;
        hd->n += 10;
    }
    
    hd->data[++hd->top] = ch;
} 

int pop(Stack hd)　　　　　　　　// 返回值为0表示空栈。
{
    if(hd->top < 0)
        return 0;
    return hd->data[hd->top--];
}
int top(Stack hd)　　　　　　　　// 返回值为0表示空栈。
{
    if(hd->top < 0)
        return 0;
    
    return hd->data[hd->top];
}

int longestValidParentheses(char* s) {
    Stack hd ;
    int i,j,k,n = strlen(s);
    int cnt,ans;

    if(s == NULL || n == 0)
    {
        return 0;
    }
    
    hd = new_stack(100);
    for(i=0; i<n; i++)
    {
        if( s[i] == '(' )       //  左侧括号放入
        {
            push(hd,s[i]);
        }
        else                    //  遇到右括号开始处理
        {
            int ch = pop(hd);      // 有4种： '('   ')'   0   负值
            if(ch == '(')   
            {
                push(hd,-2);        //说明匹配了，放进去一个-2代替()
            }
            else if(ch == 0)        //表示已经空了。无法匹配了。把)放进去作为间隔
            {
                push(hd,s[i]);
            }
            else if(ch < 0 )        //如果之前有匹配好的，
            {
                while(top(hd)<0)
                {
                    ch += pop(hd);      //拿出来匹配好的，归并成一个数
                }
                if(top(hd) == '(' )    //如果是远程匹配，又多了一个2
                {
                    ch += -2;
                    pop(hd);
                    push(hd,ch);
                }
                else                //如果确定不匹配了，把计算好的匹配数放进去，再把s[i]放进去作为间隔
                {
                    push(hd,ch);
                    push(hd,s[i]);
                }
            }
            else        // 总之是不匹配了
            {
                push(hd,s[i]);
            }
        }
    }  
    //计算栈中连续负数的最大值。

    ans = cnt =  0; 
    while(hd->top >= 0)
    {
        int ch = pop(hd);
        if(ch < 0)
        {
            cnt -= ch;
            if(cnt > ans)   ans = cnt;
        }
        else
        {
            cnt = 0;
        }
    }
    del_stack(hd);
    
    return ans;
}