统计分析模型
内容目录
- 统计分析模型概述
- 方差分析模型
- 线性回归模型
在实际的业务中,我们常常需要对一些业务问题进行建模,运用统计分析模型来解决问题,接下来我们就进入统计学习的进阶阶段,了解一下统计分析模型有哪些。
1 统计分析方法体系
变量测量尺度
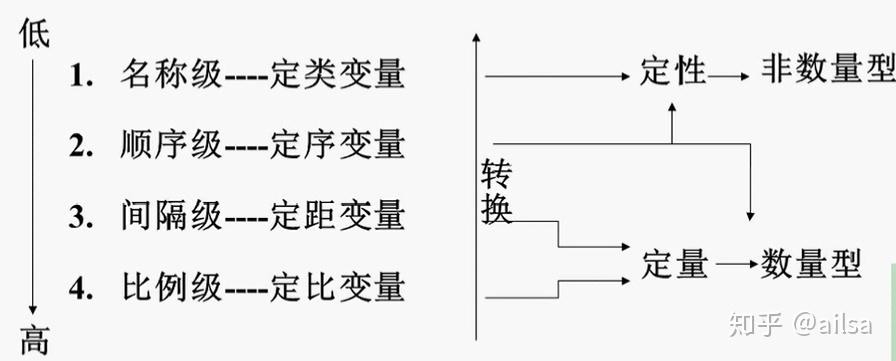
多变量统计分析方法分类
当我们需要根据某些因素(自变量)去预测结果(因变量)时,例如:根据房子的一些信息(面积,楼层,地理位置等)去预测未来的房价,并按照不同的情况分类如下:
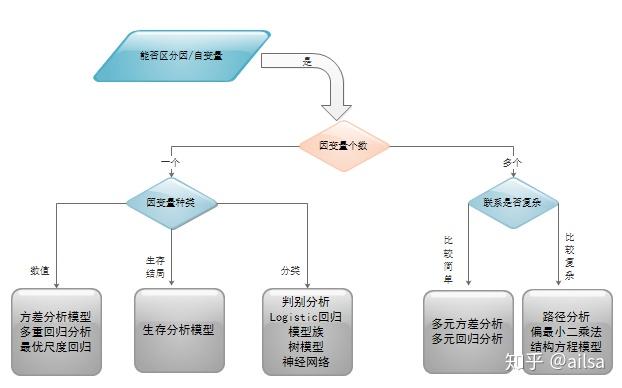
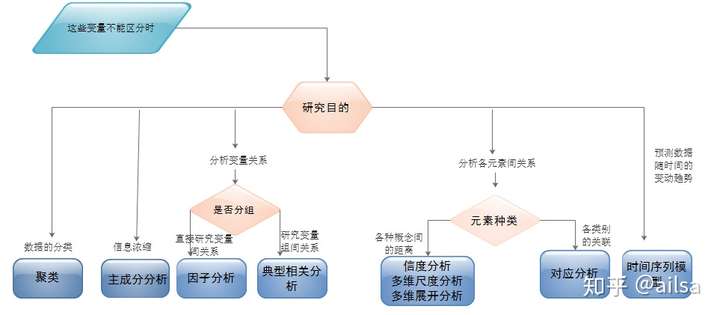
2 方差分析模型
2.1 什么是方差分析?
方差分析是在20世纪20年代发展起来的一种统计方法,它是由英国统计学家费希尔在进行实验设计时为解释实验数据而首先引入的。
方差分析(analysis of variance ANOVA) 就是通过检验各总体的均值是否相等来判断分类型自变量对数值型因变量是否有显著影响。
从定义上可以得出:在研究一个(或多个)分类型自变量与一个数值型因变量之间的关系时,方差分析就是其中的主要方法之一。他跟回归分析方法有许多相似之处,但又有本质区别。
从表面上看,方差分析是检验多个总体均值是否相等的统计分析方法,但本质上它是所研究的分类型自变量对数值型因变量的影响,例如:变量之间有没有关系,关系的强弱等问题。
方差分析根据分类型自变量的多少,分为:单因素方差分析,多因素方差分析
举个栗子
消费者协会经常会受到来到消费者对各行各业的各种投诉,现在消费者协会想研究一下,不同行业的服务质量是否存在显著差异,因此对不同行业随机不同数量的公司,抽取如下数据进行测试。
分析:从方差分析的概念中,我们知道方差分析主要判断分类型自变量对数值型因变量是否有显著影响。
这里的自变量:就是零售业、旅游业、航空公司和家电制造业
因变量:这些行业统计出来的投诉次数,
分析目的:分析不同行业对于被投诉次数是否有显著影响
数据如图:
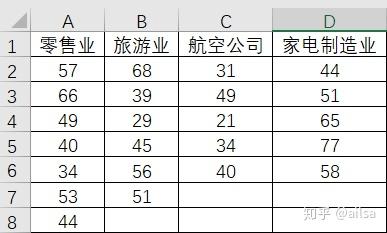
2.2 理解几个概念
因素或因子:要检验的对象,本例子中,行业是要检验的对象,因此行业就是因素,因为只有一个因素,因此称为单因素方差分析
水平或处理:因素的不同表现,零售业、旅游业、航空公司和家电制造业是行业的具体表现,就是水平或处理。
观测值:每个因子水平下得到的样本数据称为观测值,表中得出的每个行业的投诉数量则为观测值。
2.3 方差分析的基本假定
1 每个总体都应服从正态分布,例如:本例子中要求每个行业被投诉的次数必须服从正态分布
2 各个总体的方差 必须相同,也就是说,各组观察数据是从具有相同方差的正态总体中抽取的,例如:本例子中要求每个行业的方差都相同。
3 观测值是独立的。本例子中,每个企业被投诉次数与其他企业相互独立。
2.4 方差分析的原理
为了分析分类型自变量对数值型因变量的影响,需要从数据误差来源分析。
从方差分析的基本假定中可以看出,对于分类型自变量而言,他们的总体方差相同,并且服从正态分布,相当于最终比较的是他们之间的均值是否相等,如果相等,则代表来自于同一个总体,则他们之间就没有显著性差异,若均值不相等,则有可能是两个原因:
1 抽样误差造成的后果
2 他们来不同的总体,因此存在显著性差异
那我们要分析的就是从是否是抽样误差造成的入手,计算相关数据,若最终得出如果是抽样误差的概率P非常小,小于a,则代表自变量之间存在显著性差异。
2.5 单因素方差分析
方差分析中只涉及一个分类型自变量
接下来,我们进行实际操作
还是上述案例
分析不同行业对于服务质量是否存在显著差异
1.提出假设
设均值为μ
:
=
=
=
自变量对因变量没有显著影响
:
(i = 1,2,3,4) 不全相等 自变量对因变量有显著影响
2.构建检验的统计量
计算各样本均值及总体均值
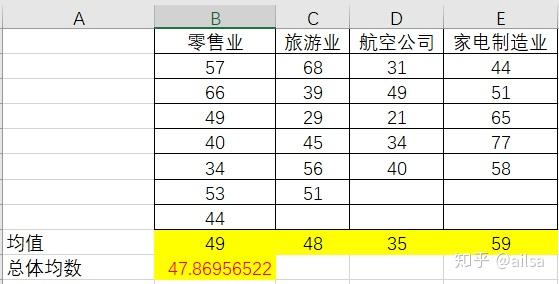
计算总误差平方和(SST)
SST 总平方和,它是全部数据与总体均值的误差平方和,是对全部数据总误差程度的度量
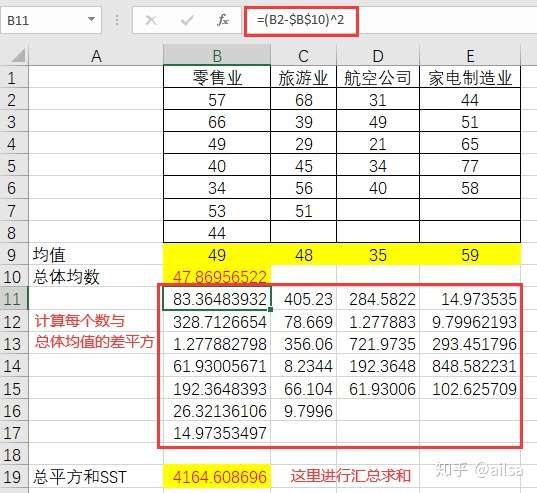
计算组间平方和(SSA)
SSA是各组均值与总体均值的误差平方和,SSA反映的是各样本之间的差异程度,又称为因素平方和,是对随机误差和系统误差大小的衡量。
计算方法:每组的均值与总均值误差平方和*改组的数据个数
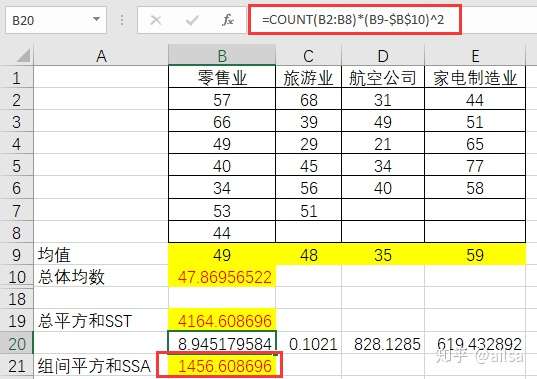
计算组内平方和(SSE)
它是每个水平或组的各样本数据与其组均值的误差平方和,反映了每个样本各观测值的离散程度。SSE是对随机误差大小的衡量,它反映了除自变量对因变量的影响因素之外,其他因素对因变量的影响,因此SSE也称为残差变量。
计算方式如下:
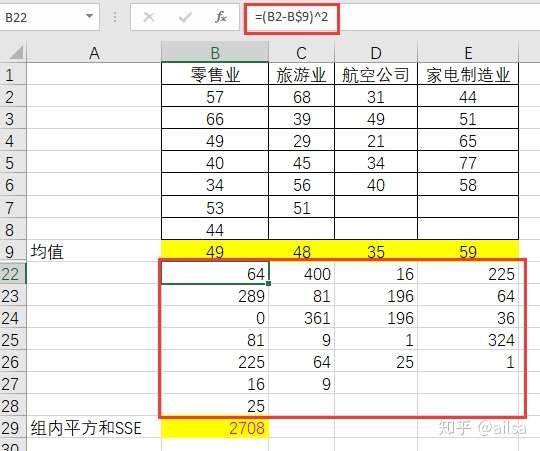
其中 三者之间的关系如下图,可通过数据验证
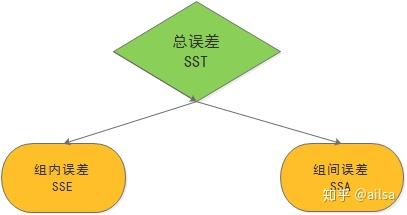
计算统计量
由于误差平方和大小与观测值有关,为了消除观测值多少对误差平方和和大小的影响,需要对其平均,也就是用平方和除以自由度,这一结果称为均方,也称为方差,三个平方和所对应的自由度分别为:
SST的自由度为n-1,其中n为全部观测值的个数,本题中n=23
SSA的自由度为k-1,其中k为因素水平(总体)的个数,本题中 k = 4
SSE的自由度为n-k
我们其实是要比较SSA与SSE,因为我们确认SSE,即组内误差来自随机误差,那我们就以SSE为基准,去比较SSA,若二者相差不大,则认为组间误差也仅仅是随机误差而没有系统误差,而由于二者之间的数量级不一样(自由度),难以直接比较,所以我们可以比较二者的均方误差:
MSA (组间均方)= =
=
=485.536231884057
MSE(组内均方) = =
=
=142.526315789474
将上述MSA与MSE对比,即得到需要的检验统计量F,当 为真时,二者的比值服从分子为自由度k-1,分母为自由度n-k的F分布
F = ~F(k-1,n-k)
计算得出F = 3.40664269047159
3 统计决策
如果原假设正确,则表明只有随机误差,没有系统误差,那MSA与MSE的差异就不会太大,反之,则代表原假设不正确,在本实例中,如果行业对被投诉次数没有影响,则四个行业的被投诉次数均值之间的差异和每个行业被投诉次数的内部差异相比,二者就不会相差太大;那现在的问题演变成计算得出的F统计量,如何去评判到底是否存在显著性差异,由于F统计量服从F分布,这时可以给定显著性水平a的临界值F与计算得出的F统计量进行对比,如何对原假设做出对应决策。
本例子中F= 3.40664269047159
假设取a = 0,05
分子自由度df = 3
分母自由度 = 19
查F表得出 (3,19) = 3.127
得出: F >
因此拒绝原假设,行业对于被投诉次数有显著影响。
有兴趣的同学还可以了解一下关系强弱的度量 的实现过程。
但是如果按照上述的步骤,计算下来实在太麻烦了,不过没关系,Excel专门提供了方差分析的功能,操作如下,简单几步,就全部实现啦
使用Excel进行方差分析
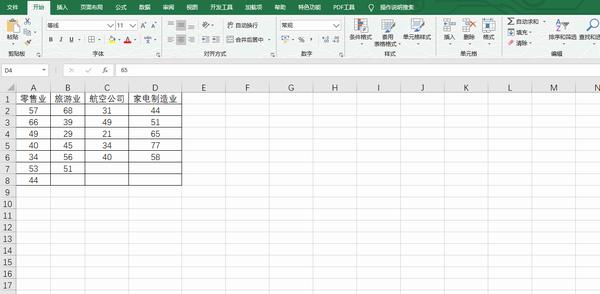
若在【数据选项卡】中未找到数据分析功能按钮,则需要单独设置
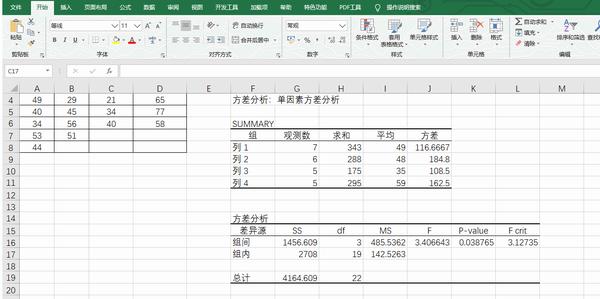
Excel得出的结果
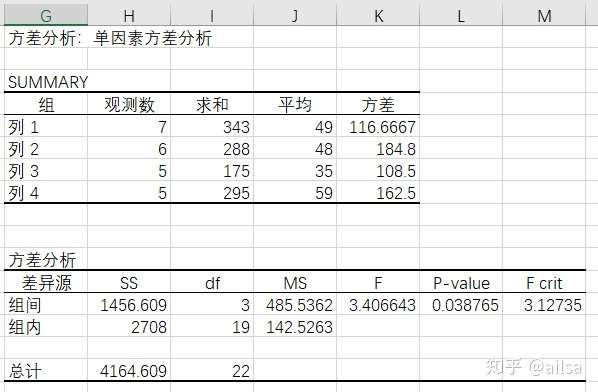
SPSS操作单因素方差分析
操作如下:
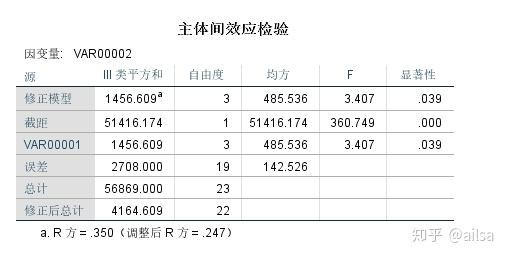
在进行决策时,可以直接利用方差分析表中的P值与显著性水平α的进行比较,若P<α,则拒绝原假设;若P>α,则不能拒绝原假设。在本题中P=0.038756<0.05,则拒绝原假设。
4 多重比较
但是我们现在只知道,他们之间有显著性差异,具体是哪些行业有差异,我们并未体现,因此需要进一步进行两两比较:
常用的方法有:
LSD法:
是由费希尔提出的最小显著差异方法(least significant difference),实际上就是t检验的变形,只是在变异和自由度的计算上利用了整个样本信息,因此仍然存在放大一错误的问题。
Scheffe(雪费)法:
当各组人数不相等,或者想进行复杂的比较时,用此方法较为稳妥,但它相对比较保守。
S-N-K法:
是运用最广泛的一种两两比较方法,它采用Student Range分布进行所有各组均值间的配对比较。该方法保证在H0真正成立时总的α水准等于实际设定值,即控制了一类错误。
下面演示scheffe检验的操作方式:
结果显示:
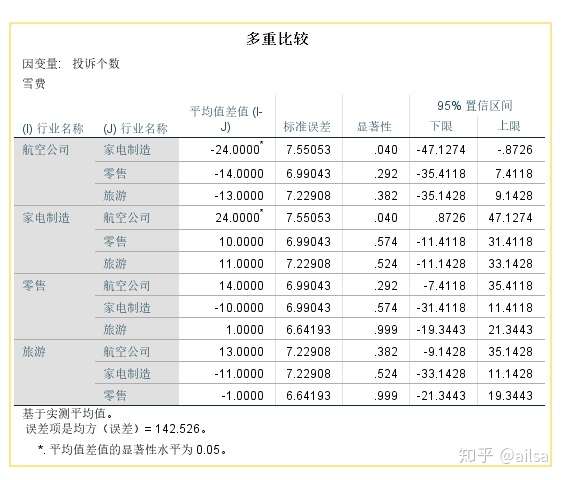
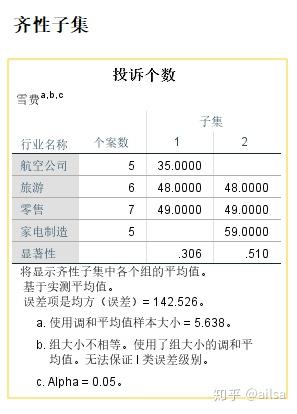
解释:处于同一列的差异不大,那从上图可以看出,航空公司与家电制造业被投诉次数之间有显著性差异
3 回归分析模型
3.1 相关分析与回归分析对比
说回归分析之前,先聊聊相关分析与回归分析的区别
相关关系:变量之间存在的不确定的数量关系,称为相关关系
先来看这幅图
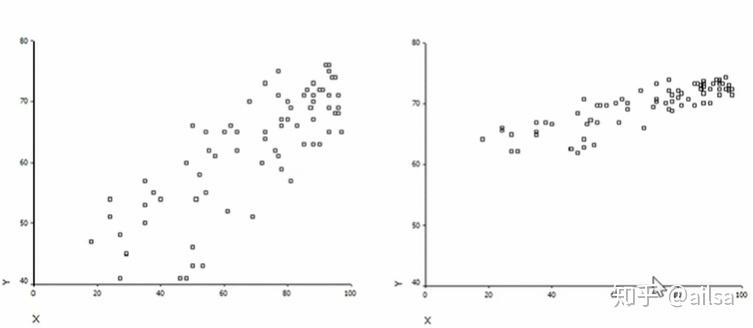
随机变量X与Y的相关系数(从协方差引申过来)
其中 Cov(X,Y) = E{[X-E(X)][Y-E(Y)]} 协方差公式。
从上图中,我们可以看出左图相对离散,右图相对集中
从相关角度分析:则右图比左图的相关性更强,呈现正相关,因为随着随机变量X变量,Y整体呈现同方向上升走势;而左图则随着X的变化,Y大体是呈上升,但会有更多的离散点。
从回归角度分析:则随着X变化,Y的变化大小左图比右图更大,它重点描述的是X变化对Y带来的具体大小的影响变化,而相关分析只能告诉你X与Y之间是否存在联系,联系的强弱如何,并不是用具体数值来体现变化的大小。
但是实际上他们描述的问题是一样的,只是各自侧重点不同而已。
回归分析和相关分析都是研究变量间关系的统计学课题,它们的差别主要是:
1、在回归分析中,y被称为因变量,处在被解释的特殊地位,而在相关分析中,x与y处于平等的地位,即研究x与y的密切程度和研究y与x的密切程度是一致的;
2、相关分析中,x与y都是随机变量,而在回归分析中,y是随机变量,x可以是随机变量,也可以是非随机的,通常在回归模型中,总是假定x是非随机的;
3、相关分析的研究主要是两个变量之间的密切程度,而回归分析不仅可以揭示x对y的影响大小,还可以由回归方程进行数量上的预测和控制.
3.2 回归分析模型介绍
研究一个连续型变量(因变量)的取值随着其他变量(自变量)的数值变化而变化的趋势
通过回归方程解释两变量之间的关系显得更为精确,可以计算出自变量改变一个单位时因变量平均改变的单位数量,这是相关分析无法做到的。
除了描述两变量的关系以外,通过回归方程还可以进行预测和控制,这在实际工作中尤为重要。
回归分析假定自变量对因变量的影响强度是始终不变的,如公式所示:
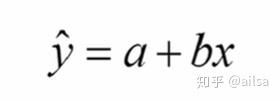
对于因变量的预测值可以被分解成两部分:
常量:x取值为0时y的平均估计量,可以被看成是一个基线水平
回归部分:它刻画因变量Y的取值中,由因变量Y与自变量X的线性关系所决定的部分,即可以由X直接估计的部分。
解释一下公式
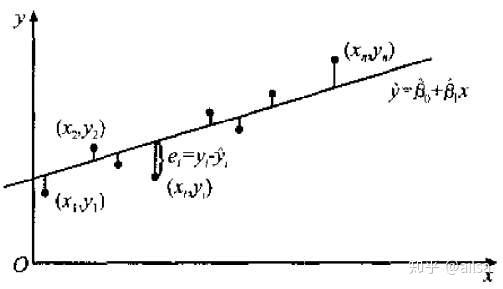
a:常数项,表示自变量取值均为0时因变量的平均水平,4回归直线在y轴上的截距
b:回归系数,在多变量回归中也称偏回归系数。自变量X改变一个单位,Y估计值的改变了,即回归直线的频率。
残差
估计值与每个实测值之间的差被称为残差。它刻画了因变量y除了自变量x以外的其他所有未进入该模型,或未知但可能与y有关的随机和非随机因素共同引起的变异,即不能由x直接估计的部分。
为了方程可以得到估计,我们往往假定 服从正态分布N(0,
)
= a + bx +
3.3 模型的几个假定条件
在一元线性回归模型中,y是x的线性函数(a+bx)加上误差项 ,a+bx反映了由于x的变化而引起的y的线性变化;
是被称为误差项的随机变量,反映了除x和y之间的线性关系之外的随机因素对y的影响,是不能由x和y的线性关系所解释的变异性,其中a和b称为模型的参数。
- 1 因变量y与自变量x之间具有线性关系
- 2 在重复抽样中,自变量x的取值是固定的,即假定x是非随机的
- 3 误差项
是一个期望值为0的随机变量
- 4 对于所有的x值,
的方差
都相同,这意味着对于一个特定的x值,y的方差也等于
- 5 误差项
是一个服从正态分布的随机变量,且独立,即
~ N(0,
)
3.4 回归方程
根据回归方程的假定, 的期望值为0,因此y的期望值E(y) =
+
x ,也就是说y的期望值是x的线性函数,因此因变量y的期望值如何变化依赖于自变量x的方程称为回归方程,一元线性回归方程的形式为:
3.5 估计回归方程
如果回归方程 和
已知,对于一个给定的x值,根据解析式可以计算出y值,但是总体回归参数往往是未知的,需要通过样本数据去估计,用样本统计量,则估计的回归方程式:
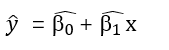
3.6 最小二乘法
观测值与估计值的差的平方和
计算出观测值与估计值的差的平方和的最小值来求未知参数的值。
3.7 判定系数
线性回归方程的最优情况,就是所有的观测点都落在这条拟合好的直线上,但是这种情况一般都不存在,那退一步讲,如果各观测点越是紧密围绕直线,说明直线对观测数据的拟合程度越好,反之越差。回归直线与各观测点的接近程度称为回归直线对数据的拟合优度,为说明直线的拟合优度,需要计算判定系数。
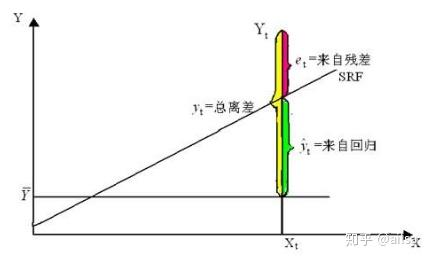
因变量y的取值是不同的,y的这种波动称为变差,变差计算可根据实际观测值y与其均值之差( -
)来表示,而n个观测值的总变差可由这些离差的平方和表示,称为总平方和,记为SST
根据图可知
因此公式可转化为
其中 是实际观测点与回归值的残差平方和,它是除了x对y的线性影响之外的其他因素引起的y的变化部分,是不能由回归直线来解释的变差部分,称为残差平方和或误差平方和,记为SSE。
看作是由于自变量x的变化引起的y的变化,而其平方和则反映了y的总体变差中由于x与y之间的线性关系引起的y的变化部分 ,它是可以由回归直线解释y的变差部分 ,记为回归平方和,SSR
总平方和(SST)= SSR(回归平方和) + SSE (残差平方和)
回归直线拟合的好坏取决于SSR及SSE的大小,或者说取决于SSR占SST的比例的大小
各观测值越靠近直线,则SSR/SST 则越大,直线拟合的越好。
回归平方和占总平方和的比例称为判定系数,记为:
判定系数 测度了回归直线对观测数据的拟合程度,取值范围[0,1],若观测值全部落在直线上,则
= 1,如果x变化y始终在均值上,则
= 0
我们之前学习的相关分析中的r,其实二者都是来判断二者相关强弱的数据,这里的r就是 的平方根,其实是一个指标啦。
案例:
分析销量的影响因素
某公司准备在国内开几家分店,于是提供了目前已开设分店的销售数据以及分店所在城市的16以上的人数,显分析一下城市所在人数对于销售的影响大小。
分析步骤如下:
做出散点图,观察变量间的趋势
操作步骤

结果如下:
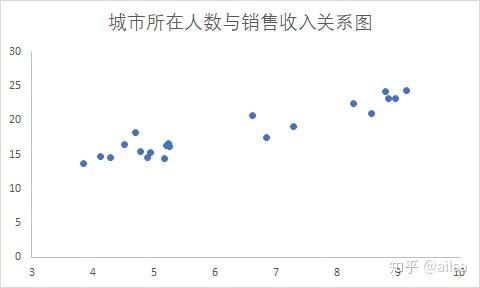
从图中可以看出,要分析是否呈现线性,是否有离群点,是否存在一定趋势
分析后大体满足
拟合模型
= a + bx +
Excel操作
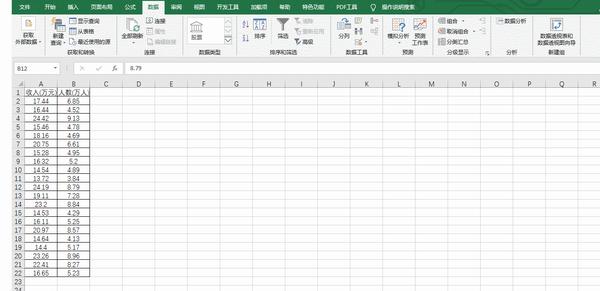
结果输出:

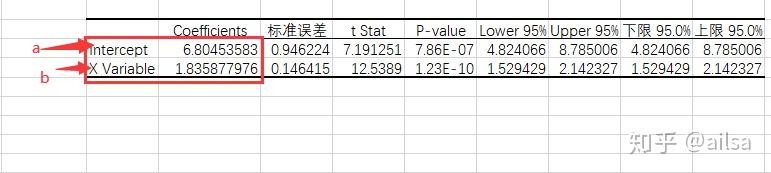
得出结果a = 6.8 ,b = 1.8
y = 6.8+1.8x
如何预测呢?
简单,把x带入,求出y值就可以啦。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号