分类数据分析

我们知道统计数据的类型分为分类数据和数值型数据，那对于分类数据而言，如果我想对其进行统计分析主要涉及哪些方面呢？

内容目录

• 分类数据的描述统计
• 分类数据的推断统计

1 分类数据的描述统计

分类数据的基本描述方式

• 频数列表
• 百分比
• 累计频数
• 累计百分比
• 众数

举个例子

以下是某个班级的小组人员数，班级总共83人，从百分比（构成比），我们可以得知每个小组人数的占比情况。

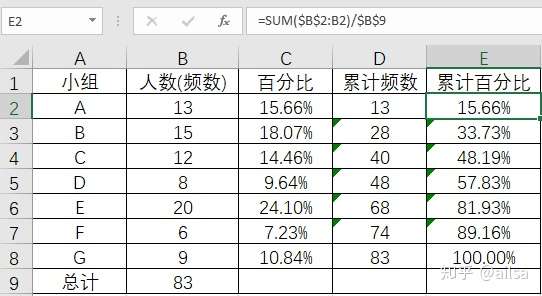
这里简单了解就可以了

2 分类数据的推断统计

对于分类数据而言，我们如果想检验变量之间是否存在某种关系，那这个就要用到 检验了

什么是卡方检验呢

对分类数据的频数进行分析的统计方法

例如：泰坦尼克号遇难的事件中，我们可以把上船人数分为男女两个类别，如图

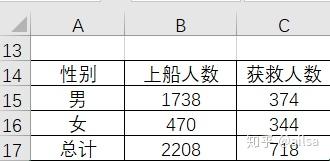
我们可以把获救人数看作频数

我们对于数值型数据还可以转换成分类数据，例如，可以把成绩按照不同水平分为不同的级别

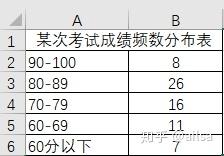
每个级别的人数就是频数

如何对分类数据的结果进行卡方检验？

我们需要通过卡方统计量来实现，先来看卡方统计量的定义

若用  表示观察值频数，用  表示期望频数，则  统计量可以写成：

举个实例来解释定义

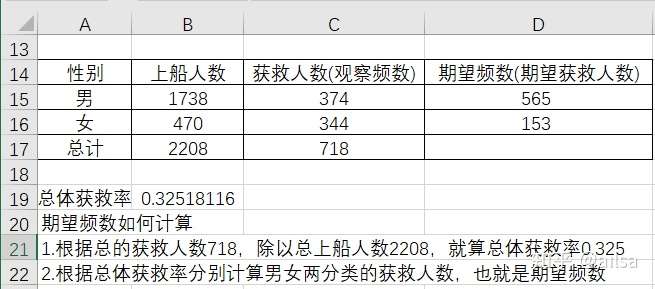
现在我们想分析一下性别对于是否获救有没有关系呢？也就是不同的性别对于是否能够存活有无影响呢？

这就需要用到拟合优度检验

拟合优度检验是针对只有一个分类变量的检验

拟合优度检验是用  统计量进行统计显著性检验的重要内容之一。它是依据总体分布情况，计算出分类变量中各类别的期望频数，与分布的观察频数进行对比，判断期望频数与观察频数是否有显著性差异，从而达到对分类变量进行分析的目的。

我们还拿刚才的例子，假设以  = 0.1的显著性水平检验存活状况与性别是否有关

解：本例中需要判断观察频数与期望频数是否一致

 ：观察频数与期望频数一致

 ：观察频数与期望频数不一致

计算过程如下：

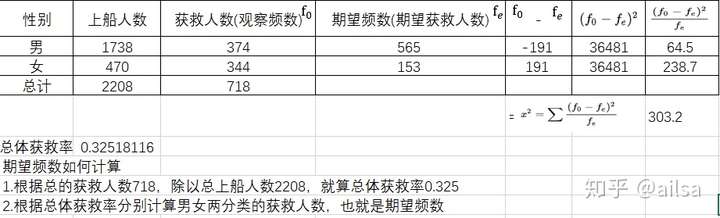
自由度的计算公式为R-1，R为分类变量的个数，这里分为男女两类，因此自由度 = 1

通过查卡方分布表可得  (1) = 2.706

因此计算结果303.2远大于2.706，所以拒绝原假设，说明性别对于是否存活有显著影响。

那对于一个分类变量的检验使用的是拟合优度检验，对于两个分类变量呢，例如分析对于原料而言，不同地区与不同等级这两个变量之间是否有关联呢？

独立性检验

首先，这种形式叫做列联表，对其进行检验叫独立性检验，是由两个以上的变量进行交叉分类的频数分布表

我们拿原料的生产地区与等级这两个变量进行分析

一种原料来自三个不同的地区，原料质量被分成三个不同的等级。从这批原料中随机抽取500件进行检验，结果如下图，要求检验各个地区和原料质量之间是否存在依赖关系（  =0.05）

 ：地区与原料等级之间是独立的（不存在依赖关系）

 ：地区与原料等级之间不独立（存在依赖关系）

1.计算交叉表的期望比率

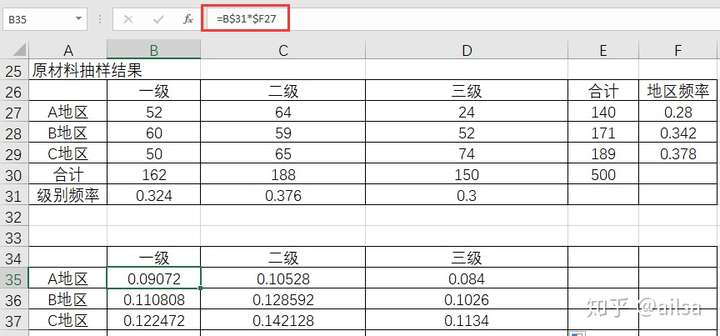
=B$31*$F27

注：每个地区的总占比跟每个等级的总占比相乘，得出3X3个结果，如上图

2.期望比率*500得出每个期望频数

=B$31*$F27*500

3.根据样本统计量公式计算结果

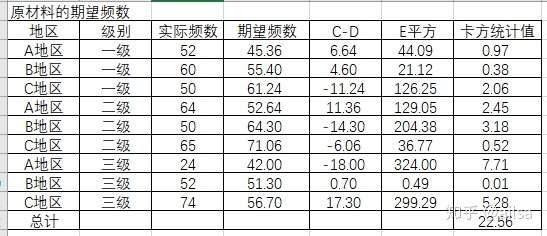
 的自由度 = （R-1）（C-1）= 2*2 = 4

自由度是两个变量分别对应的个数减1

假设  = 0.05 查卡方分布表可得  = 9.4877

由于卡方统计量远大于9.4877，所以拒绝原假设，说明材料质量与地区有关联关系。