推断统计分析
推断统计
是研究如何利用样本数据来推断总体特征的统计方法,从样本信息外推到总体,以最终获得对所感兴趣问题的解答。
内容目录
- 统计学的几个概念
- 概率分布
- 抽样分布
- 参数估计
- 假设检验
统计学的几个概念
1 变量
1 分类变量
- 无序分类变量
说明事物类别的一个名称,如性别有男女两种,二者无大小之分,无顺序之分,还有如血型、民族等
- 有序分类变量
也是说明事物类型的一个名称,但是有次序之分,例如:满意度分为满意 一般 不满意,三者是有顺序的,但是无大小之分
2 数值型变量
- 连续型变量
取值范围是一个区间,它可以在该区间中连续取值,即连续型变量可以取到区间中的任意值,并且有度量单位。例如:身高、年龄、体重、金额
- 离散型变量
取值范围是有限个值或者一个数列构成的,表示分类情况,如:企业数量 产品数量等
总结:
无序分类变量:无大小之分,无顺序之分,仅知道属于哪个类别
有序分类变量:无大小之分,但是有顺序之分,各个类别客户划分等级
连续型变量:有大小之分,一定区间范围内取值个数无法确定
离散变量:有小大之分,一定区间范围内取值个数是有限的,可数的。
2 概率
随机事件:随机现象某种可能的观察结果称为随机事件
概率:刻画随机事件发生可能性大小,取值介于0-1之间,是经过大量的重复的独立的实验而得出的结论。
- 小概率事件
在统计学中,如果随机事件发生的概率小于或等于0.05,则认为是一个小概率事件,表示该事件在大多数情况下不会发生,并且一般认为小概率事件在一次随机抽样中不会发生,这就是小概率原理。小概率原理是推断统计的基础。
经典案例:

瞎猫碰上死耗子
3 随机变量
随机事件的数量化
比如:还是抛硬币,出现正面,我们定义为“成功”,记为1,出现反面定义为“失败”,记为0,,那{0,1}就是本次实验的结果的量化值,为随机变量
离散型随机变量:随机变量X可以一一列举出来,在一定区间范围内X是有限个,可数的
例如抛硬币,X可取1或0
连续型随机变量:随机变量X无法一一列举,在一定区间范围内是无限个,
例如:统计北京市30岁以上男性身高,每个人的身高都不一样,测量单位一定的情况下,数据是连续的
4 总体和样本
总体:根据研究目的确定的所有个体某指标观察值(测量值)的集合
样本:在一个较大范围的研究对象中随机抽出一部分个体进行观察或预测,这些个体的测量值构成的集合称为样本。
大多数统计研究只能接触到样本,例如:灯泡检验是否合格只能通过样本
例:
任务
检验某批生产的所有灯泡是否达到合格率,某批生产的所有灯泡就是总体
随机从中抽取5%的灯泡进行检验,随机抽取的5%的灯泡就是样本5 随机抽样
在抽样研究中,随机抽取一部分个体进行观察和测量的过程称为随机抽样
随机抽样的本质:每个个体最终是否入选在抽样进行前是不可知的,但是其入选的可能性是确切可知的(每个个体被抽到的概率是相等的)
注:随机≠随便

暗箱中有5个球,3个黄的,2个白的,1个红的,随机抽取其中一个
街头随机采访5个人,回答单身的原因【这种真的是随机吗】
6 总体参数和统计量
总体参数:刻画总体特征的指标称为总体参数,例如:总体均值(μ),总体标准差(σ),总体比例 (π)
统计量:刻画样本特征的指标称为统计量,例如:样本均值(x-bar),样本标准差(s),样本比例(p)
但是往往总体参数都是不可知的,我们经常会通过样本统计量去估算总体参数。
7 抽样误差
许多总体指标是未知的,需要用相应的样本统计量对其进行估计。由随机抽样造成的样本统计量与总体指标之间的差异称为抽样误差(sampling error)
虽然在一次抽样研究中的抽样误差大小是随机的,但是抽样误差在概率意义下有规律可循,这种规律称为抽样分布,后面会详细讲到。
概率分布
随机变量的概率存在一定的规律,这个规律叫做概率分布,但是离散型随机变量和连续型随机变量的规律并不相同,离散型随机变量的概率分布有:二项分布、泊松分布;连续型随机变量的概率分布:正态分布。
1 离散型随机变量的概率分布
二项分布
说到二项分布,不得不提一下他的前辈:伯努利分布
伯努利实验
在现实生活中,许多事件的结果往往只有两个。例如:抛硬币,正面朝上的结果只有两个:国徽或面值;检查某个产品的质量,其结果只有两个:合格或不合格;购买彩票,开奖后,这张彩票的结果只有两个:中奖或没中奖;拨打女朋友电话:接通或没接通。。。以上这些事件都可被称为伯努利试验

伯努利试验是单次随机试验,只有"成功(值为1)"或"失败(值为0)"这两种结果,是由瑞士科学家雅各布·伯努利(1654 - 1705)提出来的。
其概率分布称为伯努利分布(Bernoulli distribution),也称为两点分布或者0-1分布,是最简单的离散型概率分布。我们记成功概率为p(0≤p≤1),则失败概率为q=1-p,则概率:
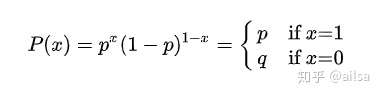
而二项分布是指在只有两个结果的n次独立的伯努利试验中,所期望的结果出现次数的概率
在单次试验中,结果A出现的概率为p,结果B出现的概率为q,p+q=1。那么在n=10,即10次试验中,结果A出现0次、1次、……、10次的概率各是多少呢?这样的概率分布呈现出什么特征呢?这就是二项分布所研究的内容。
案例:还是抛硬币,抛5次,计算2次正面朝上的概率

计算过程

假设某个试验是伯努利试验,其成功概率用p表示,那么失败的概率为q=1-p。进行n次这样的试验,成功了x次,则失败次数为n-x,发生这种情况的概率可用下面公式来计算:
二项分布公式

其中
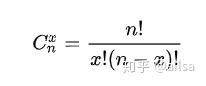
是二项式的计算方式 !表示阶乘
上述案例使用Excel计算方式:
=BINOM.DIST(2,5,0.5,FALSE)
函数介绍
BINOM.DIST(number_s,trials,probability_s,cumulative)
BINOM.DIST 函数语法具有以下参数:
- Number_s 必需。 试验的成功次数。
- Trials 必需。 独立试验次数。
- Probability_s 必需。 每次试验成功的概率。
- cumulative 必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE,则 BINOM.DIST 返回累积分布函数,即最多存在 number_s 次成功的概率;如果为 FALSE,则返回概率密度函数,即存在 number_s 次成功的概率。
二项分布的特征:
1.进行n次相同条件下的相互独立的重复试验
2.每次试验,只有2个结果,成功或者失败
3.出现成功的概率P每次试验是相同的,失败的概率q也是,并且p+q=1
如果符合上面的条件,那就是二项分布,如果上述试验只进行一次,就叫做伯努利试验,也是就二项分布是n次伯努利试验的结果。
二项分布的均值和方差分别为np和npq
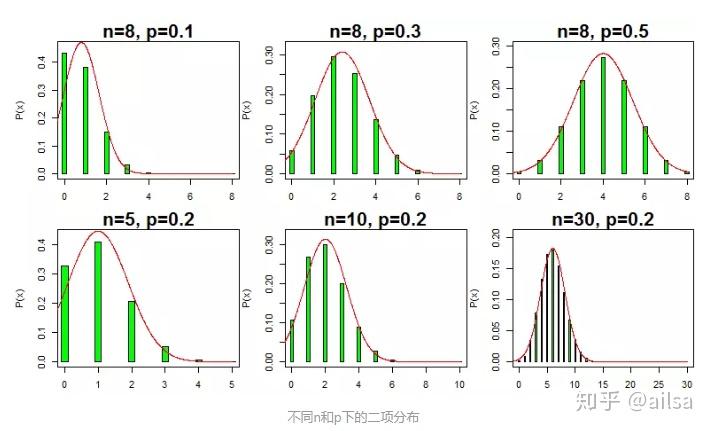
二项分布形状变化规律,可明显由下图观察出来。图中的横轴代表试验"成功"的次数;纵轴代表次数对应的概率;红线是均值为np、方差为npq的正态分布曲线。
由此可见,二项分布是一个概率分布族,随着试验次数n和成功概率p的不同而不同,且它与正态分布关系密切。
二项分布在工作中并不经常用到,不过在赌场倒是挺有用的,有想去玩一把的同学可以深入研究一下。
泊松分布

用来描述在一指定时间范围内或在指定的面积或体积内某一事件出现的次数的分布,他们对应的随机变量的概率服从的分布叫做泊松分布。
例如:
1 某企业中每月某设备出现故障的次数
2 单位时间内到达某一服务台需要服务的顾客人数
举个例子
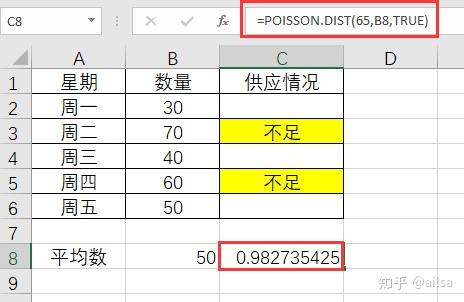
小王的婶婶新开了一个包子铺,生意还不错,但是有一天小王去买包子,看见婶婶一筹莫展,问其原因,原来是因为包子铺6点-10点营业,这一周头有两天包子蒸少了,不到8点就卖完了,后来吸取教训蒸多了,又因为卖不完而不新鲜了,早上6点-10点到底蒸多少包子合适呢?
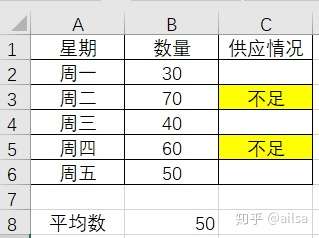
还好小王学过统计学,婶婶把馒头数据简单假设如下:

我们想一想,首先能不能用均值,我们算一下平均数

如果按照平均数,则5天中有2天都供不应求,这个不太合适
这可该怎么办?
我们换个思路,包子在6点-10点之间,每个包子的命运只有两个结果,要么卖出了,要么没卖出,那我们可以把6点-10点这个时间段当成一条有长度的线,假设分成20等份,假设每个时间段上放一个包子,要么卖出去了,要么没卖出去,类似于抛8次硬币,要么出现正面,要么出现反面,我们计算一下,卖出去7个包子的概率,利用二项分布公式
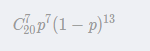
如果我们把时间段分成n等份,则卖出7个包子的概率为
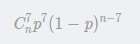
运用极限,把时间段分的越细越好,并计算在这个时间段内卖出 k 个馒头的概率为:
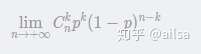
对于这个p该怎么计算呢?
我们知道它服从二项分布,二项分布的期望为np,则

因此

推导过程(了解就行):

假设每天准备65个包子,μ在这里可以直接使用均值50来计算,最后得出
概率为98.2%,其实大部分时候我们基本能满足每天的需求,因为数据量小,所有可能实际意义不是很明显,这里只是为了教学参考。
Excel使用Poisson.dist函数计算结果:
函数介绍
=POISSON.DIST(65,B8,TRUE)
POISSON.DIST(x,mean,cumulative)
POISSON.DIST 函数语法具有下列参数:
- X 必需。 事件数。
- Mean 必需。 期望值。
- cumulative 必需。 一逻辑值,确定所返回的概率分布的形式。 如果 cumulative 为 TRUE,则 POISSON.DIST 返回发生的随机事件数在零(含零)和 x(含 x)之间的累积泊松概率;如果为 FALSE,则 POISSON 返回发生的事件数正好是 x 的泊松概率密度函数。
泊松分布是二项分布的极限
在n重伯努利实验中,当成功的概率很小,实验次数很大时,二项分布可近似等于泊松分布
在实际应用中,当p<=0.25,n>20,np<=25时,用泊松分布近似二项分布的效果良好

2 连续型随机变量的概率分布
正态分布
德国的高斯

法国的拉普拉斯

回到最开始的业务场景
通过统计描述,分析师已经了解了配件A过去的日消耗量波动情况,现希望基于历史数据设定库存控制线,要求该库存量能够保证99%的使用日不会出现库存断货情况。
该怎么办呢?
控制线设置成均数可以吗?
肯定是不可以的,因为均值只是代表一般水平,换句话说,有大概一半的数据在均数以下,有一半在以上,如果把均数设置为库存控制线,最多也就只能满足50%左右的使用日不会出现库存断货情况
如果使用百分位数呢?
计算P99位置的数值,这样理论是可以的,但是百分位数对于样本量比较大的数据集才具有意义,样本量太小,实际意义不大
举个例子:零件日消耗量分布从1-100,我们随机抽取50个样本,计算P99,要求这个值要大于99%的日消耗,假设这个样本数据的最大值是80,比这个数小的是78,最终我们计算出来的是78,显然跟100差的很远,这个数据拿到实际应用中,是不满足要求的,因为样本量少造成的误差太大的缘故。
那该怎么办?
那就用到接下来要讲的内容
从频数分布到概率分布

那我们来分析一下
直方图/频率图的性质
直条的面积实质上就是频率(或者百分比)
面积=直条高度X宽度(组距) = 频率
因此直条的面积相加等于1
当样本量越来越大,频率(面积) 趋向概率
并且组距越来越小时,直方条的顶缩成点并且各个直方条的顶连接成一条曲线,这条曲线就是 概率密度分布曲线
概率密度的概念和固体的密度基本类似
哪个地方的概率大说明密度就大

这就是正态分布
官方概念

正态分布的两个重要特征:均数μ和标准差σ

μ是分布曲线的最高峰的位置(集中趋势)
σ标准差是离散程度的度量(离散趋势)
正态分布是具有对称性的
正态分布是应用最广泛的一种分布,在我们生活中正态分布随处可见
人的智商
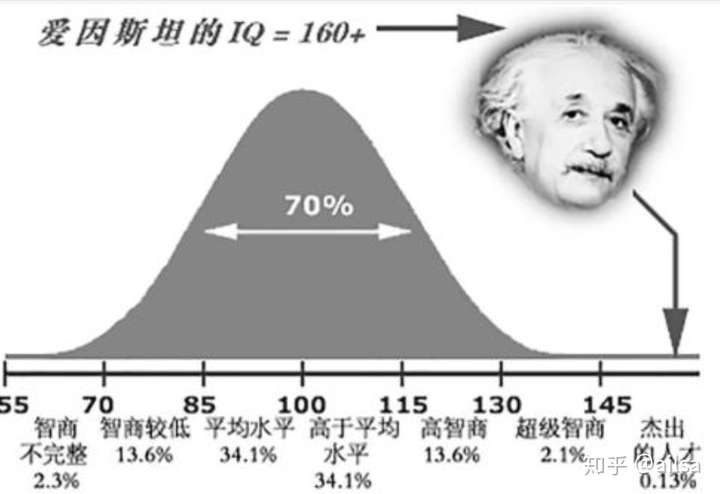
大部分人的智商是正常的,只有少数像爱伊斯坦老爷子这样的才会智商发飙
人的身高,这个是西方国家的
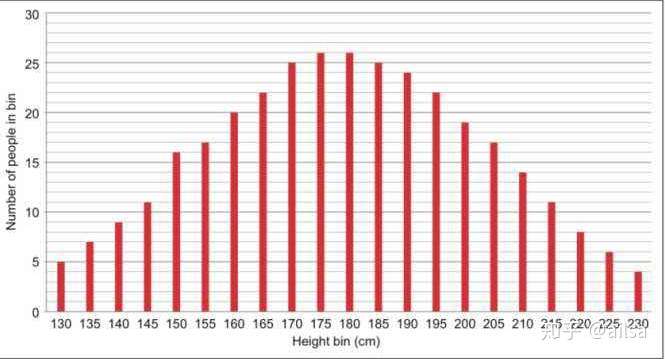
什么是标准正态分布?
不同的正态分布,其曲线下方的面积分布规律各不相同,使得在应用上很不方便,需要为每种分布单独计算曲线下面积的分布规律
为此统计学家优先计算了均数为0,标准差为1的正态分布N(0,1)曲线下面积分布规律。
其曲线下概率面积分布规律非常常用
95% 99%
双侧 1.96 2.58
单侧 1.64 2.33
95%的情况下最常用

标准正态分布的曲线下面积分布规律
只要将相应的指标转换成服从标准正态分布,就可以根据该面积分布规律计算出累积概率。
例:95%的双侧个体参考值范围

看看这张图,参考值就是应用了正态分布的知识
回到刚才的例子中
解题思路
首先确定数据是否大致服从正态分布
如果服从,直接采用正态分布公式计算参考值范围
如果不服从,那么是否可以采取某种形式进行变换成正态分布
如果还不行,只能采用百分位数,但是如果样本量小的话,数据可能不准确
举个栗子,详细看看如何根据正态分布计算区间范围
某零件的长度服从正态分布,平均长度为10mm,标准差为0.2mm,问: 从该批零件中随机抽取一件,其长度不到9.4,mm的概率是多少?
计算过程

使用Excel如何计算
=NORMDIST(9.4,10,0.2,TRUE)
函数介绍
NORMDIST(x,mean,standard_dev,cumulative)
NORMDIST 函数语法具有下列参数:
- X 必需。 需要计算其分布的数值。
- Mean 必需。 分布的算术平均值。
- standard_dev 必需。 分布的标准偏差。
- cumulative 必需。 决定函数形式的逻辑值。 如果 cumulative 为 TRUE,则 NORMDIST 返回累积分布函数;如果为 FALSE,则返回概率密度函数。
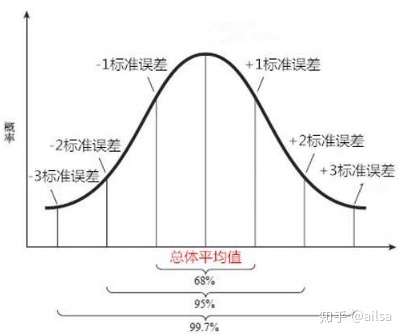
正态分布的经验法则

抽样分布
统计推断
就是根据你拥有的信息来对现实世界进行某种判断
我们在生活中的推断
可以根据一个人的衣着、言谈和举止判断其身份
看一个脸色,来判断心情好坏,身体状况
统计中的推断也不例外,只不过它是完全依据数据做出的
那什么是统计推断呢
从数据得到关于现实世界的结论的过程就叫做统计推断(statistical inference)
因为我们在实际工作中,往往只能通过样本去推估总体,所以统计推断非常重要
重要提示:任何一个总体参数都可以进行统计推断
例:配件日消耗量的均数、中位数、标准差等等,都是可以进行统计推断的
但是目前比较成熟,用的最多的就是对于均值的推断
应用场景:
基于配件A的领用历史数据,我们能否估计出其总体日均领用量的大致范围?
解决方案:
最简单的方式:样本均数就等于总体均数,但是这个到底对不对,有点太没有说服力了
给定一个范围是不是更准确一些
抽样误差与标准误
抽样误差:由样本导致的样本均数与相应的总体均数在数值上的差异
但是如何定量表达其大小?
样本均数与真实总体均数之差看上去是可以表示抽样误差大小的,但实际上无法计算
考虑在一个总体中实际上可进行无限多次抽样,实际上这些样本的抽样误差应当也服从某种分布规律
从统计总体的角度来看,其实就是要回答对于一个相同的总体,如果我们从中进行抽样研究的话,则相应的样本统计量(例如均数)的离散程度是怎样的。
例:研究人群为上海成年男性,研究指标为脉搏每分钟跳动次数
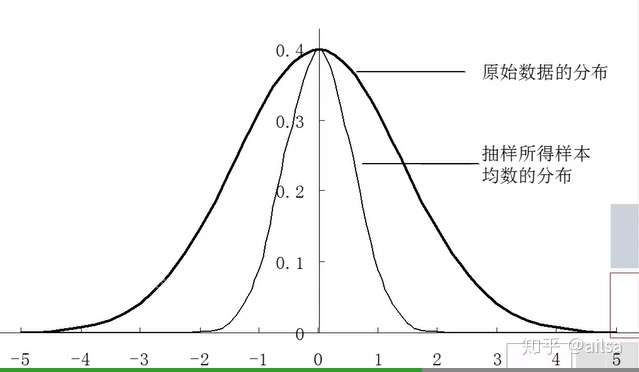
假设随机在华东地区按样本量为25抽取样本,并测量其脉搏,每个样本计算样本均数,如果重复10000次抽样,则会得到10000次样本均数
显然,样本均数存在随机变异,但在大量重复观察的情况下,可以证明同样有一定的规律,即:样本均数的概率分布。

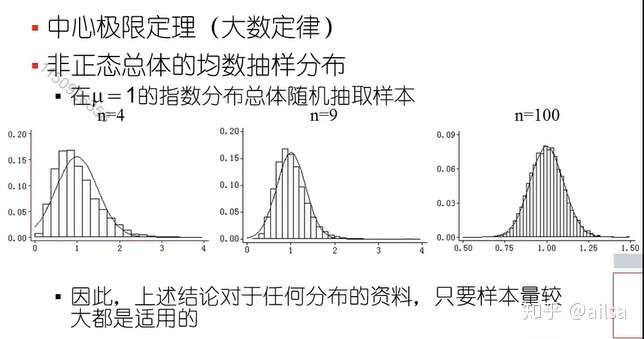
中心极限定理
设从均值为μ,方差为 (有限)的任意一个总体中抽取样本量为n样本,当n充分大时,样本均值
的抽样分布近似服从均值为μ,方差为σ^2/n的正态分布。
也就是说,你抽取n个样本,每个样本的均值近似服从的正态分布。
大数定律和中心极限定理
大数定理是在当时间发生次数趋近无穷之后,强调样本平均数会依概率收敛与原分布的期望,比如投一枚硬币正反两面都可以,正面记为1,反面为0,那么期望为0.5。当次数无穷之后(或者理解为很大)那么那么多时间的平均期望会离0.5非常近。
中心极限定理用一句话来理解,次数发生很多之后(次数要求没有大数定理的次数高),样本均值近似服从N(μ,σ²/n)的正态分布。
然后再来看,当我们中心极限定理的n次数非常大,就会发现方差无限接近于0,就意味着一直在均值附近了,那么也就是我们的大数定理了
当样本量大于等于30时,样本均数则默认是服从正态分布,对于总体是否是正态都适用。

显然,影响抽样误差大小的因素有两个
- 总体内各个体间的变异程度
- 样本含量N的大小
使用标准误,我们就可以知道如果使用样本统计量(如均数)来估计总体参数,可能的变动范围是多大,从而提高结论的实用性。
但是实际上,我们对于总体标准差并不知道,因此只能用样本标准差S来代替,从而均数标准误的估计公式为:

如果使用总体标准差进行计算,则
是服从标准正态分布的
但是如果用样本标准差进行估计,则
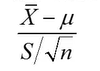
是服从t分布的
由标准正态分布推导出的其他分布:卡方分布、t分布、F分布
卡方分布
卡方分布在实际应用中主要是解决方差相关的问题
卡方分布的定义

简单来说,卡方分布就是多个标准正态分布的平方和
补充:自由度
可以自由取值的个数,当我们通过样本去推估总体时,取n个样本,自由度则为n-1,如果单纯想对样本进行计算,则自由度为n。
卡方分布的特点

卡方分布图

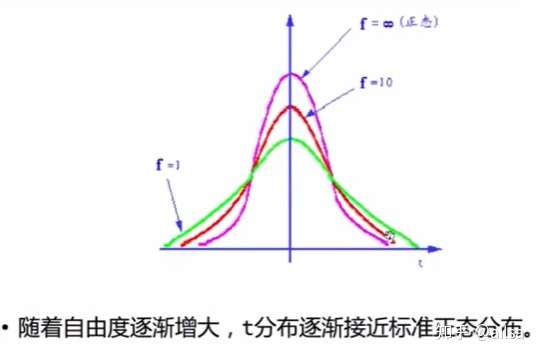
t分布

t分布的定义
若随机变量X服从标准正态分布N(0,1),随机变量Y服从自由度为n的卡方分布,且X与Y独立,则

简单来说,t分布就是标准正态分布除以均方的根,主要用于处理小样本问题
注:均方:一组数的平方和的平均值
F分布
功能:均方之比,用来对比两个方差
由统计学家费希尔首先提出的,以其姓氏的第一个字母来命名

F分布的密度函数图

参数估计
推断方法:点估计与区间估计
样本均数直接作为总体均数的点估计,但显然仅有点估计是不够的
区间估计:根据响应标准误的大小,按照一定的可信度给出一个总体参数可能的取值范围。
该区间被称为可信区间


可信区间的含义
可信度仅仅是大量重复抽样时的一个渐进概念。认为“95%的可信区间包括真实参数值的概率为0.95”
这种理解方式是错误的
计算出的可信区间是固定的,而总体参数值也是固定的。因此只有两种可能。95%的可信度只是说如何我们能够大量重复实验的话,则平均下来每100个可信区间中,会有大约95个覆盖真实值。
可信区间的实际应用
例:调查结果显示,某电视节目在观众中的收视率为90%,在95%的置信度下,抽样误差为正负3%
如何实现参数估计
绝大多数统计软件都是将参数估计功能和统计描述功能或者相应的假设检验功能整合在一起实现的

假设检验
1 为什么要做检验
- 从统计描述结果中发现可能的数据规律
- 但如果是抽样研究的样本,此时获取的只是样本的信息
- 研究者关心的并不仅仅是样本,更希望了解相应的总体特征
- 参数估计:推估样本所在的总体特征
- 假设检验:对提出的一些总体假设进行分析判断,做出统计决策
2 假设检验步骤之前需要做的工作
- 运用统计学知识根据研究设计和资料的性质正确选择分析过程
- 初步的统计描述(集中趋势、离散趋势)和统计分析
- 集中趋势:均数、中位数
- 离散趋势:标准差/方差、四分位差
- 分布特征
- 异常值及其他
3 假设检验的原理
基于小概率反证法,小概率原理,即认为小概率事件在一次随机抽样中不会发生
最经典的小概率事件:瞎猫碰到死耗子
基本思想:先建立一个关于样本所属总体的假设,考察在假设条件下随机样本的特征信息是否属于小概率事件,若为小概率事件,则怀疑假设成立有悖于该样本所提供特征信息,因此拒绝假设。
事实上,小概率事件在随机抽样中还是可能发生的,只是发生的概率很小。若正好碰上了,则假设检验的结论就是错误的,当然,犯这种错误的概率很小,是我们为了做出决策而愿意付出的代价。
举个栗子
一家大型超市连锁店上个月接到几例消费者投诉,某品牌60克装薯片包装内的土豆片太少
店方猜想引起这些投诉的原因是运输过程总沉积在食品袋底部的土豆片碎屑过多,而不是整包的重量不足,但为了保险起见,店方仍然决定对这批存货的平均重量(克)进行检验
问题:
检验多少包才合适?少了没有说服力,多了成本高
究竟差异要和60克大到什么程度才能认为确实有差异呢
这个时候就需要用到假设检验了
现有的样本均数和已知总体均数不同,其差别可能有两个方面的原因造成
- 样本来自已知总体,现有差别为抽样误差
- 样本所来自的总体与已知总体不同,存在本质差异
为了识别这两种可能,应当对其做假设检验
如何做呢?需要按照以下步骤
4 假检验的基本步骤
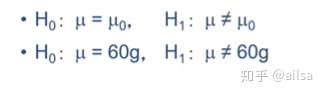
- 建立假设
根据统计推断的目的而提出对总体特征的假设
统计学中的假设有两方面的内容: 原假设:H0
备择假设:H1
原假设就是来当枪把子的,是被推翻的对象,一般是我们不希望成立的情况
备择假设:当H0被拒绝时就可以接受H1了,两者是互斥的,非此即彼
上述例子中,原假设和备择假设如下:
- 确定检验水准
实际上就是确定拒绝H0时的最大允许误差的概率
检验水准(size of test),常用a表示,是指检验假设H0本来成立,却根据样本信息拒绝H0的可能性大小,换言之,a是拒绝了实际上成立的H0的概率。
常用的检验水准为a=0.05
其意义是:在所设H0的总体中随机抽得一个样本,其均数比现有样本均数更偏离总体均数的概率不超过5%
类似于考试中习惯用的60%作为及格线
- 计算统计量和P值
实际上在此之前还有一步叫做进行验证,样本数据即从此得来
统计量只是工具,概率值才是目的,它可以客观衡量样本对假设总体偏离程度。
从H0假设的总体中抽出现有样本(及更极端情况)的概率,即P值
还是回到刚才薯片重量的问题,假设我们抽取50袋薯片,计算出的均值为58克,通过一些资料我们知道薯片的总体标准差为3克
我们知道,当样本量大于等于30时,其样本统计量服从正态分布,这里是检验均值,因此根据中心极限定理,我们可以采用z统计量来计算
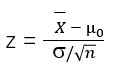
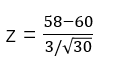
计算所得z = -3.65
查z表或者使用=NORMSDIST(3.65)得出0.9999,因为是负值,所以 p = 1-0.9999 = 0.000131
p < 0.05 因此拒绝原假设,不能肯定薯片包装的平均重量是60克
检验统计量的特点
- 该统计量应当服从某种已知的分布,从而可以计算出P值
- 各种检验方法所利用的分布及计算原理不同,从而检验统计量也不同
- 得出推断结论
按照事先确定的检验水准a界定上面得到的P值,并按小概率原理认定对H0的取舍,作出推断结论。
若P<=a
- 基于H0假设的总体情况出现了小概率事件
- 则拒绝H0,接受H1,可以认为样本与总体的差别不仅仅是抽样误差造成的,可能存在本质上的差别,属“非偶然的”,因此,可以认为两者的差别有统计学意义
- 进一步根据样本信息引申,得出实用性的结论
若P>a
- 基于H0出现了很常见的事件
- 则样本与总体间的差别尚不能排除纯碎由抽样误差造成,可能的确属“偶然的”,故尚不能拒绝H0
- 因此,认为两者的差别无统计学意义,但这并不意味着可以接受H0
尚不能认为有罪 不等于 可确认无罪
两种错误类型

检验效能:H1是真的,实际拒绝H0的概率=1-β,称为Power,又称为检验效能
我们其实往往更希望得到的是拒绝H0的结论,所以实际问题在分析时检验效能不应当太低。
5 假设检验分为单侧检验和双侧检验
双侧检验
- 不知道样本所在总体和假定总体的相应指标谁高谁低
- 得到拒绝结论更困难,因此相应的结果也更稳妥
单侧检验
- 在专业上可知所在总体的相应指标不可能更高/更低于假定总体值
- 单侧检验更为敏感,但设定单侧检验需要有充分的专业知识来支持
左单侧检验
某批发商欲从厂家购进一批灯泡,根据合同规定灯泡的使用寿命平均不能低于1000小时,已知灯泡燃烧寿命服从正态分布,标准差为200小时。在总体中随机抽取了100个灯泡,得知样本均值为960小时,批发商是否应该购买这批灯泡?
显然,灯泡的使用寿命越长越好,因此我们并不太关心灯泡大于1000小时,而是关注灯泡小于1000是否属于正常现象
原假设H0:μ>=1000
备择假设H1:μ<1000
这就是左单侧检验,也称为下限检验
计算过程:
我们知道φ(-x) = 1-φ(x)
查出p=1-0.9772 = 0.0228<0.05 拒绝原假设
右单侧检验
与之相反,不关心低于某个值,只关心高于某个值的情况,例如次品率,这里就不详细赘述
统计方法应当注意其适用条件
- 独立性(independence):各观察值间相互独立,不能互相影响
- 正态性(normality):理论上要求样本取自正态总体
- 方差齐性(homogeneity):两样本所对应的总体方差相等

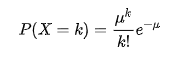
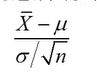

 浙公网安备 33010602011771号
浙公网安备 33010602011771号