栈,队列,双端队列,顺序表和链表
1.数据结构&算法的引言+时间复杂度
一.什么是计算机科学?
首先明确的一点就是计算机科学不仅仅是对计算机的研究,虽然计算机在科学发展的过程中发挥了重大的作用,但是它只是一个工具,一个没有灵魂的工具而已。所谓的计算机科学实际上是对问题、解决问题以及解决问题的过程中产生产生的解决方案的研究。例如给定一个问题,计算机科学家的目标是开发一个算法来处理该问题,最终得到该问题的解、或者最优解。所以说计算机科学也可以被认为是对算法的研究。因此我们也可以感受到,所谓的算法就是对问题进行处理且求解的一种实现思路或者思想。
二.如何形象化的理解算法?
- 案例引导:
一个常胜将军在作战之前都会进行战略的制定,目的是为了能够在最短的时间切成本消耗最低的情况下获取最终的胜利。如果将编码作为战场,则程序员就是这场战役的指挥官,你如何可以将你的程序可以在最短且消耗资源最小的情况下获取最终的执行结果呢?算法就是我们的策略!
- 意义所在:
- 数据结构和算法思想的通用性异常的强大,在任何语言中都被使用,它们将会是我们编码生涯中伴随我们最长久利器(左膀右臂)。有一定经验的程序员最终拼的就是算法和数据结构。
- 数据结构和算法思想也可以帮助我们拓展和历练编码的思维,可以让我们更好的融入到编程世界的角角落落。
三.什么是算法分析?
- 案例引入:刚接触编程的学生经常会将自己编写的程序和别人的程序做比对,获取在比对的过程中会发现双方编写的程序很相似但又各不相同。那么就会出现一个有趣的现象:两组程序都是用来解决同一个问题的,但是两组程序看起来又各不相同,那么哪一组程序更好呢?例如下述代码:
def sumOfN(n): theSum = 0 for i in range(1,n+1): theSum = theSum + i return theSum print(sumOfN(10))
def foo(tom): fred = 0 for bill in range(1,tom+1): barney = bill fred = fred + barney return fred print(foo(10))
分析:
- 哪个函数更好,答案取决于你的标准。如果你关注可读性,函数 sumOfN 肯定比 foo 好。事实上,你可能已经在介绍编程的课程中看到过很多例子,他们的目标之一就是帮助你编写易于阅读和理解的程序。然而,在本课程中,我们对算法本身的表示更感兴趣(当然我们希望你继续努力编写可读的,易于理解的代码)。
- 算法分析是基于每种算法使用的计算资源量来比较算法。我们比较两个算法,说一个比另一个算法好的原因在于它在使用资源方面更有效率,或者仅仅使用的资源更少。从这个角度来看,上面两个函数看起来很相似。它们都使用基本相同的算法来解决求和问题。
- 问题:a+b+c = 1000 a**2 + b**2 = c**2 (a,b,c均为自然数),求出a,b,c可能的组合?
for a in range(0,1001): for b in range(0,1001): for c in range(0,1001): if a**2+b**2 == c**2 and a+b+c==1000: print(a,b,c)
for a in range(0,1001): for b in range(0,1001): c = 1000 - a - b if a**2+b**2 == c**2 and a+b+c==1000: print(a,b,c)
分析:很明显上述两中问题的解决方案是不同的。那如何判定上述两种解决方案(算法)的优劣呢?有同学会说,观察计算两种算法使用耗费计算机资源的大小和它们的执行效率呀!但是我想说的是,一些较为复杂的算法,它耗费计算机资源的大小和执行效率我们很难能够直观的从算法的编码上分析出来。所以我们必须采用某种量化的方式求出不同算法的资源耗费和执行效率的具体值来判定算法之间的优劣。问题来了,如何进行量化计算呢?方法有两种:
- 方法1:计算算法执行的耗时(不推荐)。
import time start_time = time.time() for a in range(0,1001): for b in range(0,1001): for c in range(0,1001): if a**2+b**2 == c**2 and a+b+c==1000: print(a,b,c) end_time = time.time() print(end_time-start_time) #执行结果为: 0 500 500 200 375 425 375 200 425 500 0 500 1221.7778379917145
import time start_time = time.time() for a in range(0,1001): for b in range(0,1001): c = 1000 - a - b if a**2+b**2 == c**2 and a+b+c==1000: print(a,b,c) end_time = time.time() print(end_time-start_time) #执行结果为: 0 500 500 200 375 425 375 200 425 500 0 500 1.410386085510254
注意:单靠执行时间可以反应算法的效率吗?不能。跟机器(执行环境)存在很大关系。
方法2:计算算法的时间复杂度(推荐)
- 时间复杂度:量化算法需要的操作或者执行步骤的数量。
四.时间复杂度
- 我们试图通过算法的执行时间来判定算法的优劣。但是仅仅根据执行时间判定算法优劣有些片面,因为算法是独立于计算机的。重要的是量化算法需要的操作或者步骤的数量。选择适当的基本计算单位是个复杂的问题,并且将取决于如何实现算法。对于先前的求和算法,一个比较好的基本计算单位是对执行语句进行计数。
- 在 sumOfN 中,赋值语句的计数为 1(theSum = 0) 加上 n 的值(我们执行 theSum=theSum+i 的次数)。我们通过函数 T 表示 T(n)=1+n。参数 n 通常称为“问题的规模”,我们称作 “T(n) 是解决问题大小为 n 所花费的时间,即 1+n 步长”。在上面的求和函数中,使用 n 来表示问题大小是有意义的。我们可以说,100,000 个整数和比 1000 个问题规模大。因此,所需时间也更长。我们的目标是表示出算法的执行时间是如何相对问题规模大小而改变的。
- 计算机科学家更喜欢将这种分析技术进一步扩展。事实证明,操作步骤数量不如确定 T(n) 最主要的部分来的重要。换句话说,当问题规模变大时,T(n) 函数某些部分的分量会超过其他部分。函数的数量级表示了随着 n 的值增加而增加最快的那些部分。
- 数量级通常称为大O符号,写为 O(f(n))。它表示对计算中的实际步数的近似。函数 f(n) 提供了 T(n) 最主要部分的表示方法。T(n)的最主要部分是:在上述示例中,T(n)=1+n。当 n 变大时,常数 1 对于最终结果变得越来越不重要。如果我们找的是 T(n) 的近似值,我们可以删除 1。因此T(n)中最主要的部分为n,因此f(n)=n。因此在sumOfN函数对应的算法的时间复杂度可即为O(f(n)),即为O(n)。
- 另外一个示例,假设对于一些算法,确定的步数是 T(n)=5n^2+27n+1005。当 n 很小时, 例如 1 或 2 ,常数 1005 似乎是函数的主要部分。然而,随着 n 变大,n^2 这项变得越来越重要。事实上,当 n 真的很大时,其他两项在它们确定最终结果中所起的作用变得不重要。当 n 变大时,为了近似 T(n),我们可以忽略其他项,只关注 5n^2 。系数 5 也变得不重要。我们说,T(n) 具有的数量级为 f(n)=n^2,或者 O( n^2 )。
1 a=5 2 b=6 3 c=10 4 for i in range(n): 5 for j in range(n): 6 x = i * i 7 y = j * j 8 z = i * j 9 for k in range(n): 10 w = a*k + 45 11 v = b*b 12 d = 33
分析:前三行赋值语句执行操作步骤为3,5-8行的执行操作步骤为3n,结合第四行的外部循环,整个内外循环的执行步骤为3n^2。9-11行为2n,12行为1。最终得出T(n)=3+3n^2+2n+1,简化操作后T(n)=3n^2+2n+4。通过查看指数,我们可以看到 n^2 项是最重要的,因此这个代码段是 O(n^ 2)。当 n 增大时,所有其他项以及主项上的系数都可以忽略。
四.数据结构:
- 对于数据(基本类型的数据(int,float,char))的组织方式就被称作为数据结构。数据结构解决的就是一组数据如何进行保存,保存形式是怎样的。
- 案例:需要存储一些学生的学生信息(name,score),那么这些数据应该如何组织呢?查询某一个具体学生的时间复杂度是什么呢?
- 组织形式1:
[{'name':'zhangsan','score':100},
{'name':'lisi','score':99}
]
- 组织形式2:
[('zhangsan',100), ('lisi',99) ]
- 组织形式3:
{'zhangsan':{'score':100},
'lisi':{'score':99}
}
- 三种组织形式基于查询的时间复杂度分别为:O(n),O(n),O(1)
- 发现:python中的字典,列表,元组本身就是已经被封装好的一种数据结构啦。使用不同的数据结构进行数据的存储,所导致的时间复杂度是不一样。因此认为算法是为了解决实际问题而设计的,数据结构是算法需要处理问题的载体。
2.python数据结构的性能分析
一.引言
- 现在大家对 大O 算法和不同函数之间的差异有了了解。本节的目标是告诉你 Python 列表和字典操作的 大O 性能。然后我们将做一些基于时间的实验来说明每个数据结构的花销和使用这些数据结构的好处。重要的是了解这些数据结构的效率,因为它们是本博客实现其他数据结构所用到的基础模块。本节中,我们将不会说明为什么是这个性能。在后面的博文中,你将看到列表和字典一些可能的实现,以及性能是如何取决于实现的。
二.列表:
- python 的设计者在实现列表数据结构的时候有很多选择。每一个这种选择都可能影响列表操作的性能。为了帮助他们做出正确的选择,他们查看了最常使用列表数据结构的方式,并且优化了实现,以便使得最常见的操作非常快。
- 在列表的操作有一个非常常见的编程任务就是是增加一个列表。我们马上想到的有两种方法可以创建更长的列表,可以使用 append 方法或拼接运算符。但是这两种方法那种效率更高呢。这对你来说很重要,因为它可以帮助你通过选择合适的工具来提高你自己的程序的效率。
- 让我们看看四种不同的方式,我们可以生成一个从0开始的n个数字的列表。首先,我们将尝试一个 for 循环并通过创建列表,然后我们将使用 append 而不是拼接。接下来,我们使用列表生成器创建列表,最后,也是最明显的方式,通过调用列表构造函数包装 range 函数。
def test1(): l = [] for i in range(1000): l = l + [i] def test2(): l = [] for i in range(1000): l.append(i) def test3(): l = [i for i in range(1000)] def test4(): l = list(range(1000))
- 下面我们来使用timeit模块来计算上述四种方式的平均运行时长是多少:
- timeit模块:该模块可以用来测试一段python代码的执行速度/时长。
- Timer类:该类是timeit模块中专门用于测量python代码的执行速度/时长的。原型为:class timeit.Timer(stmt='pass',setup='pass')。
- stmt参数:表示即将进行测试的代码块语句。
- setup:运行代码块语句时所需要的设置。
- timeit函数:timeit.Timer.timeit(number=100000),该函数返回代码块语句执行number次的平均耗时。
- 案例:
from timeit import Timer #被测试的代码块 def func(n): sum = 0 for i in range(0,100): sum += i print(sum) if __name__ == "__main__": #参数2:因为参数1必须为字符串且表示的是即将被测试代码块函数的名字,因此参数2必须设置为执行参数1函数所需的设置 t = Timer('func(10)','from __main__ import func') print(t.timeit(1000))
- 使用timeit模块来计算上述四种方式的平均运行时长是多少:
t1 = Timer("test1()", "from __main__ import test1") print("concat ",t1.timeit(number=1000), "milliseconds") t2 = Timer("test2()", "from __main__ import test2") print("append ",t2.timeit(number=1000), "milliseconds") t3 = Timer("test3()", "from __main__ import test3") print("comprehension ",t3.timeit(number=1000), "milliseconds") t4 = Timer("test4()", "from __main__ import test4") print("list range ",t4.timeit(number=1000), "milliseconds") concat 6.54352807999 milliseconds append 0.306292057037 milliseconds comprehension 0.147661924362 milliseconds list range 0.0655000209808 milliseconds
注意:你上面看到的时间都是包括实际调用函数的一些开销,但我们可以假设函数调用开销在四种情况下是相同的,所以我们仍然得到的是有意义的比较。因此,拼接字符串操作需要 6.54 毫秒并不准确,而是拼接字符串这个函数需要 6.54 毫秒。你可以测试调用空函数所需要的时间,并从上面的数字中减去它。剩下的基于列表的其他操作大家也可以使用timeit进行平均耗时的测量计算。
- 列表的相关操作的方法都是被封装好的,我们没有必要对相关操作的底层算法时间进行分析,下面直接给出大家一张基于列表操作的时间复杂度的表,供大家参考:
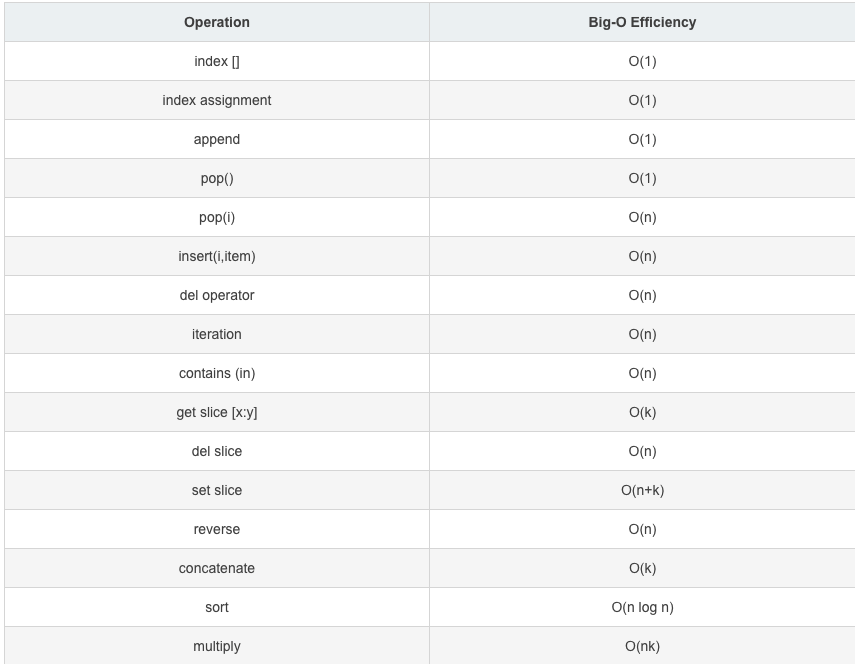
三.字典
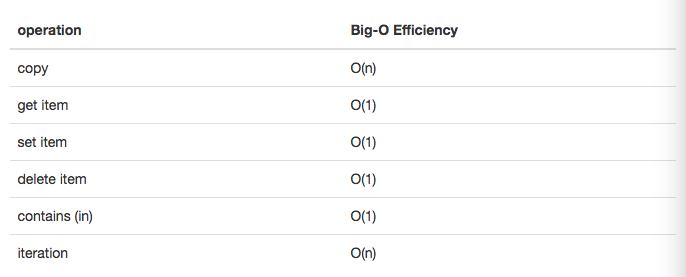
- python 中第二个主要的数据结构是字典。你可能记得,字典和列表不同,你可以通过键而不是位置来访问字典中的项目。
- 字典的时间复杂度:
3.基本数据结构-栈
一.线性数据结构
- 我们从四个简单但重要的概念开始研究数据结构。栈,队列,deques(双向队列), 列表是一类数据的容器,它们数据元素之间的顺序由添加或删除的顺序决定。一旦一个数据元素被添加,它相对于前后元素一直保持该位置不变。诸如此类的数据结构被称为线性数据结构。
- 线性数据结构有两端,有时被称为左右,某些情况被称为前后。你也可以称为顶部和底部,名字都不重要。将两个线性数据结构区分开的方法是添加和移除元素的方式,特别是添加和移除元素的位置。例如一些结构允许从一端添加元素,另一些允许从另一端移除元素。
二.栈
- 概念:栈(有时称为“后进先出栈”)是一个元素的有序集合,其中添加移除新元素总发生在同一端。这一端通常称为“顶部”。与顶部对应的端称为“底部”。栈的底部很重要,因为在栈中靠近底部的元素是存储时间最长的。最近添加的元素是最先会被移除的。这种排序原则有时被称为 LIFO,后进先出。它基于在集合内的时间长度做排序。较新的项靠近顶部,较旧的项靠近底部。
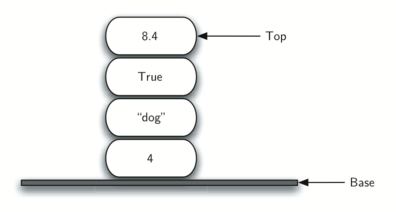
- 案例:栈的例子很常见。几乎所有的自助餐厅都有一堆托盘或盘子,你从顶部拿一个,就会有一个新的托盘给下一个客人。想象桌上有一堆书, 只有顶部的那本书封面可见,要看到其他书的封面,只有先移除他们上面的书。下图展示了另一个栈,包含了很多 Python 对象。
- 栈的分析与应用:
- 分析:和栈相关的最有用的想法之一来自对它的观察。假设从一个干净的桌面开始,现在把书一本本叠起来,你在构造一个栈。考虑下移除一本书会发生什么。移除的顺序跟刚刚被放置的顺序相反。栈之所以重要是因为它能反转项的顺序。插入跟删除顺序相反。
- 应用:每个 web 浏览器都有一个返回按钮。当你浏览网页时,这些网页被放置在一个栈中(实际是网页的网址)。你现在查看的网页在顶部,你第一个查看的网页在底部。如果按‘返回’按钮,将按相反的顺序浏览刚才的页面。
三.Python实现栈
- 栈的抽象数据类型定义:栈的抽象数据类型应该由以下结构和操作定义。栈操作如下:
-
- Stack() 创建一个空的新栈。 它不需要参数,并返回一个空栈。
- push(item)将一个新项添加到栈的顶部。它需要 item 做参数并不返回任何内容。
- pop() 从栈中删除顶部项。它不需要参数并返回 item 。栈被修改。
- peek() 从栈返回顶部项,但不会删除它。不需要参数。 不修改栈。
- isEmpty() 测试栈是否为空。不需要参数,并返回布尔值。
- size() 返回栈中的 item 数量。不需要参数,并返回一个整数。
- 代码实现:Python 中的列表类提供了有序集合机制和一组方法。例如,如果我们有列表 [2,5,3,6,7,4],我们只需要确定列表的哪一端将被认为是栈的顶部。一旦确定,可以使用诸如 append 和 pop 的列表方法来实现操作。
class Stack: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def push(self, item): self.items.append(item) def pop(self): return self.items.pop() def peek(self): return self.items[len(self.items)-1] def size(self): return len(self.items)
- 应用:
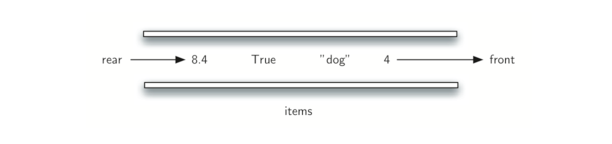
from basic.stack import Stack s=Stack() print(s.isEmpty()) s.push(4) s.push('dog') print(s.peek()) s.push(True) print(s.size()) print(s.isEmpty()) s.push(8.4) print(s.pop()) print(s.pop()) print(s.size())
4.基本数据结构-队列
一.队列
- 概念:队列是项的有序结合,其中添加新项的一端称为队尾,移除项的一端称为队首。当一个元素从队尾进入队列时,一直向队首移动,直到它成为下一个需要移除的元素为止。最近添加的元素必须在队尾等待。集合中存活时间最长的元素在队首,这种排序成为 FIFO,先进先出,也被成为先到先得。
- 案例:队列的最简单的例子是我们平时不时会参与的列。排队等待电影,在杂货店的收营台等待,在自助餐厅排队等待(这样我们可以弹出托盘栈)。行为良好的线或队列是有限制的,因为它只有一条路,只有一条出路。不能插队,也不能离开。你只有等待了一定的时间才能到前面。
- 队列的应用:我们的计算机实验室有 30 台计算机与一台打印机联网。当学生想要打印时,他们的打印任务与正在等待的所有其他打印任务“一致”。第一个进入的任务是先完成。如果你是最后一个,你必须等待你前面的所有其他任务打印。我们将在后面更详细地探讨这个有趣的例子。
除了打印队列,操作系统使用多个不同的队列来控制计算机内的进程。下一步做什么的调度通常基于尽可能快地执行程序和尽可能多的服务用户的排队算法。此外,当我们敲击键盘时,有时屏幕上出现的字符会延迟。这是由于计算机在那一刻做其他工作。按键的内容被放置在类似队列的缓冲器中,使得它们最终可以以正确的顺序显示在屏幕上。
二.Python实现队列
- 队列的抽象数据类型定义:队列的抽象数据类型应该由以下结构和操作定义。队列操作如下:
-
- Queue() 创建一个空的新队列。 它不需要参数,并返回一个空队列。
- enqueue(item) 将新项添加到队尾。 它需要 item 作为参数,并不返回任何内容。
- dequeue() 从队首移除项。它不需要参数并返回 item。 队列被修改。
- isEmpty() 查看队列是否为空。它不需要参数,并返回布尔值。
- size() 返回队列中的项数。它不需要参数,并返回一个整数。
class Queue: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def enqueue(self, item): self.items.insert(0,item) def dequeue(self): return self.items.pop() def size(self): return len(self.items)
- 使用:
>>> q.size() 3 >>> q.isEmpty() False >>> q.enqueue(8.4) >>> q.dequeue() 4 >>> q.dequeue() 'dog' >>> q.size() 2
- 面试题:如何实现两个队列生成一个栈
q1 = Queue() q2 = Queue() alist = [1,2,3,4,5] #将数据加入队列 for i in alist: q1.enqueue(i) while True: while q1.size() > 1: item = q1.dequeue() q2.enqueue(item) print(q1.dequeue()) q1,q2 = q2,q1 if q1.size() == 0: break
5.队列的应用案例
烫手山芋游戏介绍:6个孩子围城一个圈,排列顺序孩子们自己指定。第一个孩子手里有一个烫手的山芋,需要在计时器计时1秒后将山芋传递给下一个孩子,依次类推。规则是,在计时器每计时7秒时,手里有山芋的孩子退出游戏。该游戏直到剩下一个孩子时结束,最后剩下的孩子获胜。请使用队列实现该游戏策略,排在第几个位置最终会获胜。
- 这个游戏相当于著名的约瑟夫问题,一个一世纪著名历史学家弗拉维奥·约瑟夫斯的传奇故事。故事讲的是,他和他的 39 个战友被罗马军队包围在洞中。他们决定宁愿死,也不成为罗马人的奴隶。他们围成一个圈,其中一人被指定为第一个人,顺时针报数到第七人,就将他杀死。约瑟夫斯是一个成功的数学家,他立即想出了应该坐到哪才能成为最后一人。
分析:为了模拟这个圈,我们可以使用队列。假设游戏开始时,排在队列中的第一个(队首)的孩子手里拿着山芋。游戏开始后,拿着山芋的孩子出队列然后再入队列,将山芋传递给下一个孩子。每当山芋到队首孩子手里后,队首的孩子先出队列再入队列,一次类推。当传递六次后,手里有山芋的孩子淘汰,游戏继续,继续传递山芋。
from basic.queue import Queue def hotPotato(namelist, num): simqueue = Queue() for name in namelist: simqueue.enqueue(name) while simqueue.size() > 1: for i in range(num): kid = simqueue.dequeue() simqueue.enqueue(kid) simqueue.dequeue() return simqueue.dequeue() print(hotPotato(["Bill","David","Susan","Jane","Kent","Brad"],7))
6.基本数据结构-双端队列(Deque)
一.双端队列(Deque)
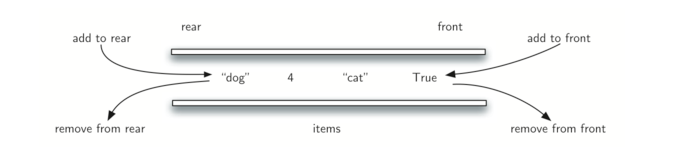
- 概念:deque(也称为双端队列)是与队列类似的项的有序集合。它有两个端部,首部和尾部,并且项在集合中保持不变。
- 特性:deque 特殊之处在于添加和删除项是非限制性的。可以在前面或后面添加新项。同样,可以从任一端移除现有项。在某种意义上,这种混合线性结构提供了单个数据结构中的栈和队列的所有能力。
- 注意:即使 deque 可以拥有栈和队列的许多特性,它不需要由那些数据结构强制的 LIFO 和 FIFO 排序。这取决于你如何持续添加和删除操作。
二.Python实现Deque
- Deque的抽象数据类型定义:Deque的抽象数据类型应该由以下结构和操作定义。其中元素可以从首部或尾部的任一端添加和移除。Deque操作如下:
-
- Deque() 创建一个空的新 deque。它不需要参数,并返回空的 deque。
- addFront(item) 将一个新项添加到 deque 的首部。它需要 item 参数 并不返回任何内容。
- addRear(item) 将一个新项添加到 deque 的尾部。它需要 item 参数并不返回任何内容。
- removeFront() 从 deque 中删除首项。它不需要参数并返回 item。deque 被修改。
- removeRear() 从 deque 中删除尾项。它不需要参数并返回 item。deque 被修改。
- isEmpty() 测试 deque 是否为空。它不需要参数,并返回布尔值。
- size() 返回 deque 中的项数。它不需要参数,并返回一个整数。
class Deque: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def addFront(self, item): self.items.append(item) def addRear(self, item): self.items.insert(0,item) def removeFront(self): return self.items.pop() def removeRear(self): return self.items.pop(0) def size(self): return len(self.items)
7.Deque的应用案例-回文检查
- 回文检测:设计程序,检测一个字符串是否为回文。
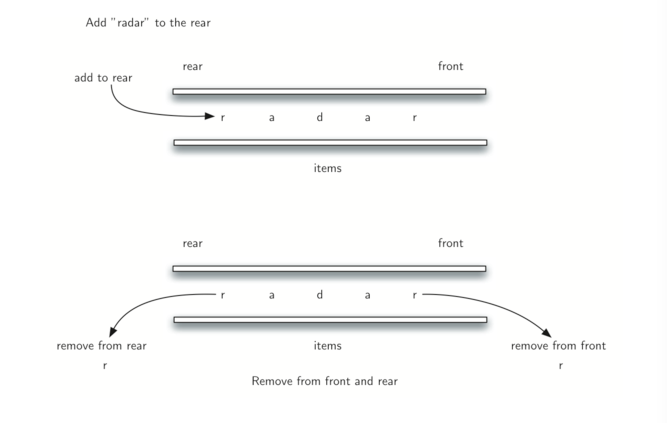
- 回文:回文是一个字符串,读取首尾相同的字符,例如,radar toot madam。
- 分析:该问题的解决方案将使用 deque 来存储字符串的字符。我们从左到右处理字符串,并将每个字符添加到 deque 的尾部。在这一点上,deque 像一个普通的队列。然而,我们现在可以利用 deque 的双重功能。 deque 的首部保存字符串的第一个字符,deque 的尾部保存最后一个字符。我们可以直接删除并比较首尾字符,只有当它们匹配时才继续。如果可以持续匹配首尾字符,我们最终要么用完字符,要么留出大小为 1 的deque,取决于原始字符串的长度是偶数还是奇数。在任一情况下,字符串都是回文。
from basic.deque import Deque def palchecker(aString): chardeque = Deque() for ch in aString: chardeque.addRear(ch) stillEqual = True while chardeque.size() > 1 and stillEqual: first = chardeque.removeFront() last = chardeque.removeRear() if first != last: stillEqual = False return stillEqual print(palchecker("lsdkjfskf")) print(palchecker("radar"))
8.基本数据结构-顺序表和链表
一.内存
- 计算机的作用:对数据进行存储和运算。首先我们需要知道我们目前使用的计算机都是二进制的计算机,就以为着计算机只可以存储和运算二进制的数据。例如下载好的一部电影,该电影可以存储到计算机中,计算机中存储的是基于二进制的电影数据,然后我们可以通过相关的视频播放软件结合相关的硬件对电影的二进制数据进行相关的运算操作,所产生的结果就是我们可以看到电影的画面和听到音频的声音。
- 问题:阐述计算机如何计算1+2的结果?
- 阐述:简单理解为,首先可以将1和2输入到计算机中,然后计算机会将1和2转换成二进制的数据进行数据存储,然后通过加法器进行两个二进制数值的计算并返回结果。
- 分析:上述的阐述中提到,计算机首先需要存储1和2这两个数值,那么计算机如何进行数据的存储呢?那么毫无疑问,计算机可以将数据直接存储到内存中。
- 变量:我们在编程世界中,可以将某个数值直接赋值给一个变量,但是最终数值会被存储到计算机的内存中,因此我们可以理解为,变量表示的就是计算机中进行数据存储的某一块内存。
- 如何形象化的理解计算机的内存?
- 举例:将计算机的内存空间映射到我们现实生活中的话,内存就好比是我们在现实生活中三维立体的空间。生活在北京的北漂们,几乎都居住的是一个独立的公寓或者合租在一个几居室的某一个房间中,那么北漂甲就好比是数据,而他所居住的房间则就是存储数据的一块内存空间。
- 分析:从上述案例中,我们可以得知北漂甲居住的房间会有两个基本的属性,其一就是房间空间的大小,其二就是房间的一个位置标识(门牌号)。那么计算机中存储数据的内存空间也会有这两个最基本的属性:内存空间大小和内存空间的地址。内存空间的大小可以表示该空间可以存储数据值的大小范围,内存空间的地址(用十六进制数值表示)可以用来通过寻址定位、查找到该内存空间中所存储的数据值。
- 如何理解 a = 10 这条赋值语句对应的内存图呢?
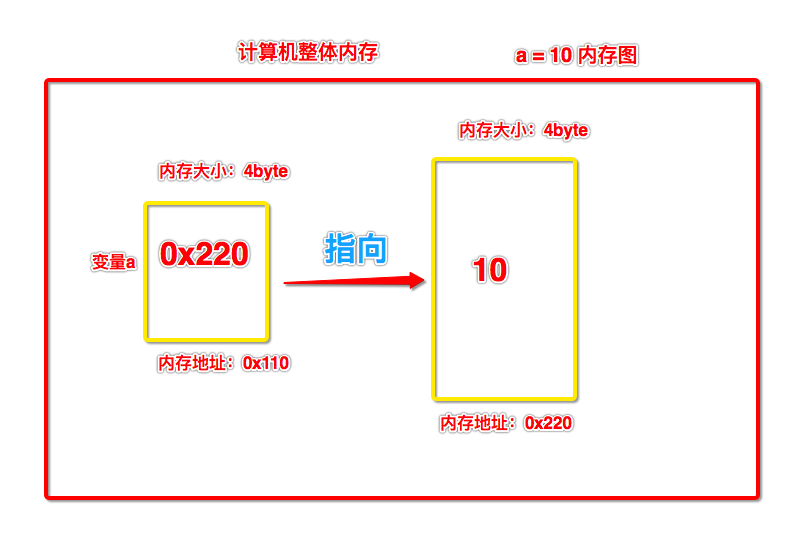
- 引用:当一个变量中存储的是某一块内存空间的地址,则该变量即可成为那块内存空间的引用。a=10,a就是10所在内存空间的一个引用。
- 指向:当一个变量中存储了一块内存空间的地址,则称该变量(引用)指向了那块内存。
- 不同类型数据占用内存空间的大小:整形(4字节),浮点型(8字节),字符型(1字节)
二.顺序表:集合中存储的元素是有顺序的。顺序表的结构可以分为两种形式:单数据类型和多数据类型。
- 单数据类型:在内存中如何存储 int a = 10,20,30,如何取得每一个数据值呢?
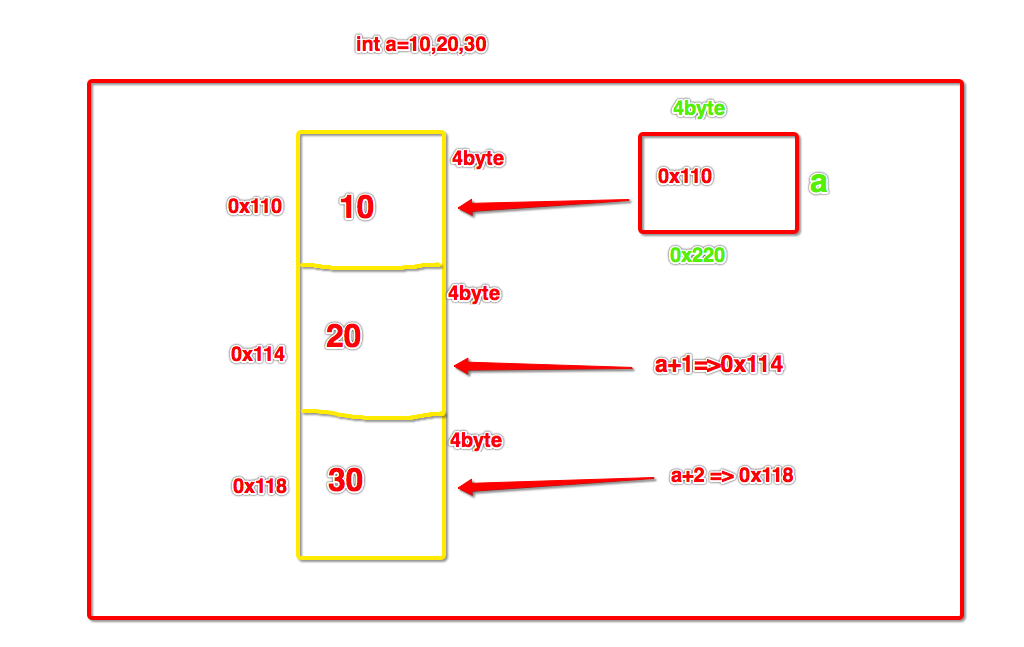
- 多数据类型:在内存中如何存储 li = 10,'a',96.5,如何获取每一个数据值呢?

- 顺序表的弊端:顺序表的结构需要预先知道数据大小来申请连续的存储空间,而在进行扩充时又需要进行数据的搬迁。
- Python中的 list 和 tuple 两种类型采用了顺序表的实现技术。
三.链表:相对于顺序表,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。
- 链表(Linked list)是一种常见的基础数据结构,是一种线性表,但是不像顺序表一样连续存储数据,而是每一个结点(数据存储单元)里存放下一个结点的信息(即地址):

- 1、单向链表
单向链表也叫单链表,是表中最简单的一种形式,它的每个节点包含两个域,一个信息域(元素域)和一个链接域。这个链接指向链表中的下一个节点,而最后一个节点的链接域则指向一个空值。
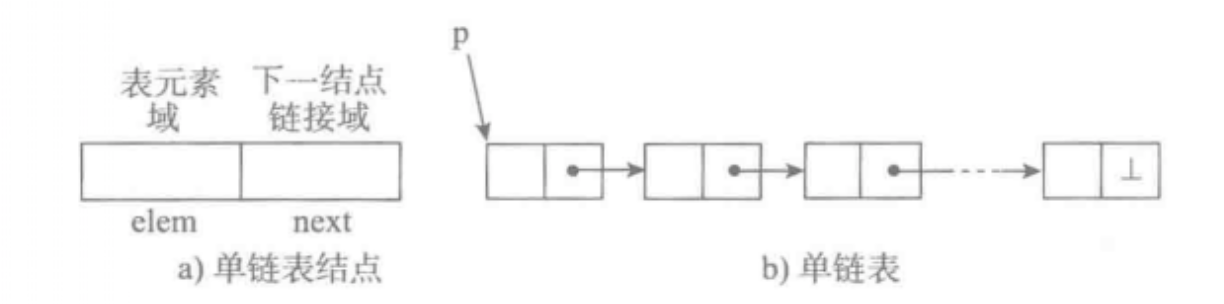
- 表中元素elem用来存放具体的数据。
- 链接域next用来存放下一个节点的位置。
- 变量p指向链表的头节点(首节点)的位置,从p出发能找到表中的任意节点。
- 单向链表的抽象数据类型定义:
. is_empty():链表是否为空
. length():链表长度
. travel():遍历整个链表
. add(item):链表头部添加元素
. append(item):链表尾部添加元素
. insert(pos, item):指定位置添加元素
. remove(item):删除节点
. search(item):查找节点是否存在
- 代码实现:
class Node(): def __init__(self,item): self.item = item self.next = None def __str__(self): return str(self.item) class Link(): def __init__(self): #永远指向链表中第一个节点 self._head = None def isEmpty(self): return self._head is None def add(self,item): node = Node(item) node.next = self._head self._head = node def length(self): count = 0 if self.isEmpty(): return count else: cur = self._head while cur is not None: count += 1 cur = cur.next return count def travel(self): cur = self._head while cur is not None: print(cur) cur = cur.next def append(self,item): node = Node(item) cur = self._head if self.isEmpty(): self._head = node else: while cur is not None: #因为循环遍历结束后cur会指向空并非最后一个节点 pre_cur = cur cur = cur.next pre_cur.next = node def search(self,item): ex = False cur = self._head while cur is not None: if cur.item == item: ex = True break cur = cur.next return ex def insertTo(self,item,index): cur = self._head ex = 0 node = Node(item) #插入到第一个节点位置 if index <= 0: self.add(item) #插入到最后一个节点位置 elif index >= self.length(): self.append(item) else: while cur is not None: pre = cur cur = cur.next #此处插入的一定不是第一个节点和最后一个节点位置,因此index要减1 if ex == index-1: node.next = cur pre.next = node break ex += 1 def remove(self,item): pre = None cur = self._head #删除的是第一个节点 if cur.item == item: self._head = cur.next else: while cur is not None: pre = cur cur = cur.next if cur.item == item: pre.next = cur.next cur.next = None cur = cur.next #测试代码 link = Link() link.add('bobo') link.add('jay') link.add('tom') link.add('jerry') # print(link.search('tom')) # link.insertTo('haha',1) link.remove('bobo') link.travel()
- 2.单向循环链表:单链表的一个变形是单向循环链表,链表中最后一个节点的next域不再为None,而是指向链表的头结点。

- 基本操作和单链表基本一样,实现代码如下:
# coding=utf-8 # 单向循环链表 class Node: """节点""" def __init__(self, item): self.item = item self.next = None def __str__(self): return str(self.item) class SinCycLinkedList: """单向循环链表""" def __init__(self): self._head = None def is_empty(self): """判断链表是否为空""" return self._head is None def length(self): """链表长度""" if self.is_empty(): return 0 count = 1 cur = self._head while cur.next != self._head: # print("cur", cur.item) count += 1 cur = cur.next return count def travel(self): """遍历""" if self.is_empty(): return cur = self._head print(cur.item) while cur.next != self._head: cur = cur.next print(cur.item) def add(self, item): """在头部添加一个节点""" node = Node(item) if self.is_empty(): self._head = node node.next = self._head else: node.next = self._head cur = self._head while cur.next != self._head: cur = cur.next cur.next = node self._head = node def append(self, item): """在尾部添加一个节点""" node = Node(item) if self.is_empty(): self._head = node node.next = self._head else: cur = self._head # print(type(cur), cur.item, cur.next) while cur.next != self._head: cur = cur.next # print(cur.item) cur.next = node node.next = self._head def insert(self, pos, item): """指定位置pos添加节点""" if pos <= 0: self.add(item) elif pos > (self.length() - 1): self.append(item) else: node = Node(item) cur = self._head cur_pos = 0 while cur.next != self._head: if (pos - 1) == cur_pos: node.next = cur.next cur.next = node break cur_pos += 1 cur = cur.next def remove(self, item): """删除一个节点""" if self.is_empty(): return pre = self._head # 删除首节点 if pre.item == item: cur = pre while cur.next != self._head: cur = cur.next cur.next = pre.next # 删除首节点(跳过该节点) self._head = pre.next # 重新指定首节点 # 删除其他的节点 else: cur = pre while cur.next != self._head: if cur.next.item == item: cur.next = cur.next.next cur = cur.next def search(self, item): """查找节点是否存在""" if self.is_empty(): return -1 cur_pos = 0 cur = self._head if cur.item == item: return cur_pos while cur.next != self._head: if cur.item == item: return cur_pos cur_pos += 1 cur = cur.next if cur_pos == self.length() - 1: return -1 if __name__ == "__main__": ll = SinCycLinkedList() ll.add(1) # 1 ll.add(2) # 2 1 # ll.travel() ll.append(3) # 2 1 3 ll.insert(2, 4) # 2 1 4 3 ll.insert(4, 5) # 2 1 4 3 5 ll.insert(0, 6) # 6 2 1 4 3 5 print("length:", ll.length()) # 6 ll.travel() # 6 2 1 4 3 5 print("search(3)", ll.search(3)) # 4 print("search(7)", ll.search(7)) # -1 print("search(6)", ll.search(6)) # 0 print("remove(1)") ll.remove(1) print("length:", ll.length()) # 6 2 4 3 5 print("remove(6)") ll.remove(6) ll.travel()
3.双向链表:一种更复杂的链表是 "双向链表" 或 "双面链表"。每个节点有两个链接:一个指向前一个节点,当次节点为第一个节点时,指向空值;而另一个指向下一个节点,当此节点为最后一个节点时,指向空值。

- 代码实现:
# coding=utf-8 # 双向链表 class Node: """节点""" def __init__(self, item): self.item = item self.prev = None self.next = None class DLinkList: """双向链表""" def __init__(self): self._head = None def is_empty(self): """判断链表是否为空""" return self._head is None def length(self): """获取链表长度""" if self.is_empty(): return 0 else: cur = self._head count = 1 while cur.next is not None: count += 1 cur = cur.next return count def travel(self): """遍历链表""" print("↓↓" * 10) if self.is_empty(): print("") else: cur = self._head print(cur.item) while cur.next is not None: cur = cur.next print(cur.item) print("↑↑" * 10) def add(self, item): """链表头部添加节点""" node = Node(item) if self.is_empty(): self._head = node else: cur = self._head node.next = cur cur.prev = node self._head = node def append(self, item): """链表尾部添加节点""" node = Node(item) if self.is_empty(): self._head = node else: cur = self._head # 遍历找到最后一个节点 while cur.next is not None: cur = cur.next # 在尾节点添加新的节点 cur.next = node node.prev = cur def insert(self, pos, item): """指定位置添加""" # 头部添加 if pos <= 0: self.add(item) # 尾部添加 elif pos > (self.length() - 1): self.append(item) # 其他位置添加 else: node = Node(item) cur = self._head cur_pos = 0 while cur.next is not None: if cur_pos == (pos - 1): # 与下一个节点互相指向 node.next = cur.next cur.next.prev = node # 与上一个节点互相指向 cur.next = node node.prev = cur cur_pos += 1 cur = cur.next def remove(self, item): """删除节点""" if self.is_empty(): return else: cur = self._head # 删除首节点 if cur.item == item: self._head = cur.next cur.next.prev = None # 删除其他节点 else: while cur.next is not None: if cur.item == item: # 删除之前:1 ←→ [2] ←→ 3 # 删除之后:1 ←→ 3 cur.prev.next = cur.next cur.next.prev = cur.prev cur = cur.next # 删除尾节点 if cur.item == item: cur.prev.next = None def search(self, item): """查找节点是否存在""" if self.is_empty(): return -1 else: cur = self._head cur_pos = 0 while cur.next is not None: if cur.item == item: return cur_pos cur_pos += 1 cur = cur.next if cur_pos == (self.length() - 1): return -1 if __name__ == "__main__": ll = DLinkList() ll.add(1) # 1 ll.add(2) # 2 1 ll.append(3) # 2 1 3 ll.insert(2, 4) # 2 1 4 3 ll.insert(4, 5) # 2 1 4 3 5 ll.insert(0, 6) # 6 2 1 4 3 5 print("length:", ll.length()) # 6 ll.travel() # 6 2 1 4 3 5 print("search(3)", ll.search(3)) print("search(4)", ll.search(4)) print("search(10)", ll.search(10)) ll.remove(1) print("length:", ll.length()) ll.travel() print("删除首节点 remove(6):") ll.remove(6) ll.travel() print("删除尾节点 remove(5):") ll.remove(5) ll.travel()
- 面试题:如何将单链表倒序?
def reverse(self): if self._head: cur = self._head pre = None cur_next = cur.next if cur.next is None: return while True: cur.next = pre pre = cur cur = cur_next if cur == None: self._head = cur break cur_next = cur_next.next self._head = pre


 浙公网安备 33010602011771号
浙公网安备 33010602011771号