降维方法介绍整理：SVD,PCA,LDA等

SVD降维

SVD（Singular Value Decomposition，奇异值分解）是对矩阵进行分解，假如待分解的矩阵A是一个m*n矩阵，那么对矩阵A的SVD分解即：A=U∑V^T。

其中U是一个m*m的矩阵；Σ是一个m*n的矩阵，Σ除了主对角线上的元素以外其他元素全为0，主对角线上元素称为奇异值；V是一个n*n矩阵。

将A视为一个线性变换，可以将A分解为旋转+拉伸+旋转的线性变换【左乘一个正交矩阵是旋转，左乘一个对角阵是拉伸变换】

→ 

 

如何求解SVD

 

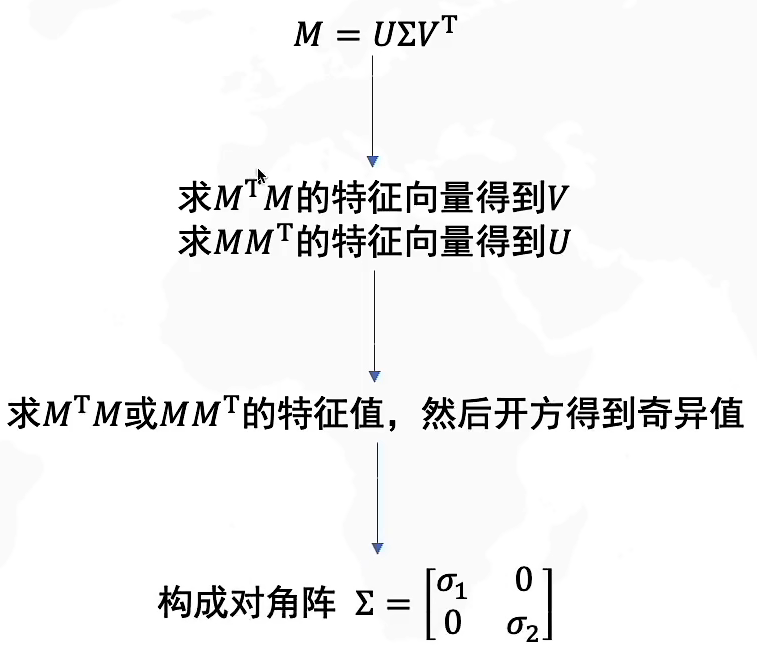
 SVD和PCA主成分的关系

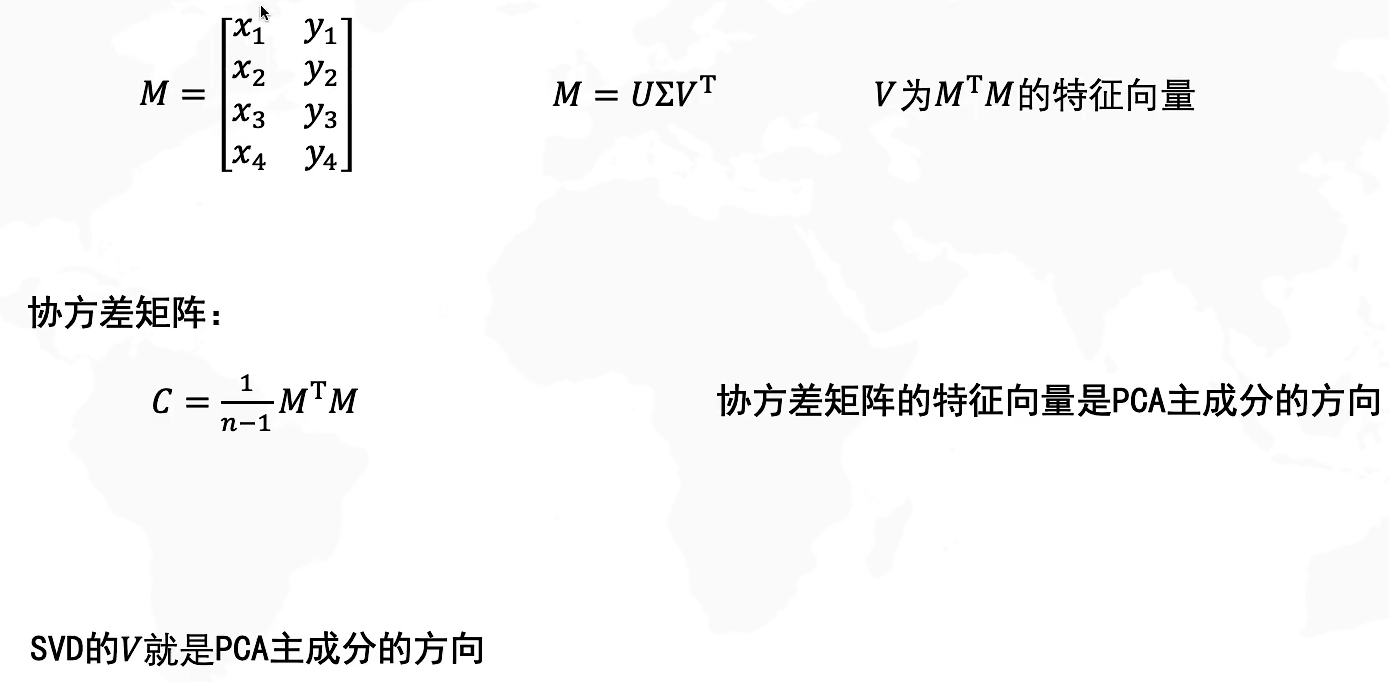
SVD在计算过程中原矩阵的维度其实是不变的 ，但是在取n%的奇异值时，重新计算回去的原矩阵中元素值显著降低，秩也降低，整体来看数据得到了压缩和衰减；或许可以理解为一种降维吧。

PCA降维：

• 两个矩阵相乘的意义是将右边矩阵中的每一列向量a_i变换到左边矩阵中以每一行行向量为基所表示的空间中去。
• 如何选择基才是最优的。一种直观的看法是：希望投影后的投影值尽可能分散，因为如果重叠就会有样本消失。当然这个也可以从熵的角度进行理解，熵越大所含信息越多。
• 数值的分散程度，可以用数学上的方差来表述。于是上面的问题被形式化表述为：寻找一个一维基，使得所有数据变换为这个基上的坐标表示后，方差值最大。
• 在一维空间中我们可以用方差来表示数据的分散程度。对于高维数据，我们用协方差进行约束，协方差可以表示两个变量的相关性。为了让两个变量尽可能表示更多的原始信息，我们希望它们之间不存在线性相关性，因为相关性意味着两个变量不是完全独立，必然存在重复表示的信息。
• 降维问题的优化目标：将一组 N 维向量降为 K 维，其目标是选择 K 个单位正交基，使得原始数据变换到这组基上后，各变量两两间协方差为 0，而变量方差则尽可能大（在正交的约束下，取最大的 K 个方差）。
• 优化目标变成了寻找一个矩阵 P，满足PCP^T是一个对角矩阵，并且对角元素按从大到小依次排列，那么 P 的前 K 行就是要寻找的基，用 P 的前 K 行组成的矩阵乘以 X 就使得 X 从 N 维降到了 K 维并满足上述优化条件。

设有 m 条 n 维数据。

1. 将原始数据按列组成 n 行 m 列矩阵 X；
2. 将 X 的每一行进行零均值化，即减去这一行的均值；
3. 求出协方差矩阵  ；
4. 求出协方差矩阵的特征值及对应的特征向量；
5. 将特征向量按对应特征值大小从上到下按行排列成矩阵，取前 k 行组成矩阵 P；
6.  即为降维到 k 维后的数据。

LDA降维（有监督）

思想：将数据投影到低维空间之后，使得同一类数据尽可能的紧凑，不同类的数据尽可能的分散。因此，LDA算法是一种有监督的机器学习算法。

LDA有如下两个假设：(1)原始数据根据样本均值进行分类。(2)不同类的数据拥有相同的协方差矩阵。当然，在实际情况中，不可能满足以上两个假设。但是当数据主要是由均值来区分的时候，LDA一般都可以取得很好的效果。LDA降维最多降到类别数k-1的维数。

假设投影直线是向量ω,则对任意一个样本x_i,它在直线ω的投影为ω^Tx_i,对于我们的两个类别的中心点μ0，μ1,在在直线ω的投影为ω^Tμ0，ω^Tμ1。由于LDA需要让不同类别的数据的类别中心之间的距离尽可能的大，也就是我们要最大化  ,同时我们希望同一种类别数据的投影点尽可能的接近，也就是要同类样本投影点的协方差  和  尽可能的小，即最小化  。综上所述，优化目标为：

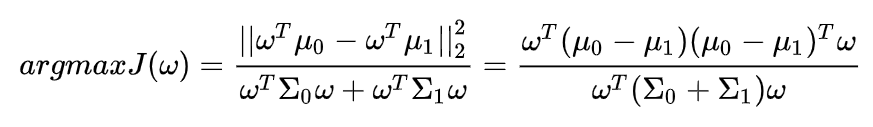
类内散度矩阵  为：

类间散度矩阵  为：

优化目标重新定义：

LDA算法流程

1. 计算类内散度矩阵S_ω

2. 计算类间散度矩阵S_b
3. 计算矩阵
4. 计算  的最大的d个特征值和对应的d个特征向量  得到投影矩阵W
5. 对样本集中的每一个样本特征  ,转为新的样本 
6. 得到输出样本集 

ICA降维

动机源自于cocktail party problem（鸡尾酒会问题），ICA与被称为盲源分离(Blind Source Separation,BSS)或盲信号分离的方法具有非常密切的关系。“源”在此处的意思是指原始信号，即独立成分，如鸡尾酒会中的说话者；而“盲”表示我们对于混合矩阵所知甚少，仅仅对源信号做非常弱的假定。

ICA假设的三个条件

• 独立成分被假设是统计独立。对于这一条可以从概率密度以及其他算法可以判断。我们说随机变量y₁，y₂..y_n独立，是指在i≠j时，有关y_i的取值情况对于y_j如何取值没有提供任何信息。
• 独立成分具有非高斯分布。如果观测到的变量具有高斯分布，那么ICA在本质上是不可能实现的。假定S经过混合矩阵A后，他们的联合概率密度仍然不变化，因此我们没有办法在混合中的得到混合矩阵的信息。
• 假设混合矩阵是方阵。这个条件是为了后续ICA算法求解的便利。当混合矩阵A是方阵时就意味着独立源的个数和监测信号的个数数目是一致。

ICA算法步骤

观测信号构成一个混合矩阵，通过数学算法进行对混合矩阵A的逆进行近似求解分为三个步骤：

1) 去均值。去均值也就是中心化，实质是使信号X均值是零。
2) 白化。白化就是去相关性。
3) 构建正交系统。在常用的ICA算法基础上已经有了一些改进，形成了fastICA算法。fastICA实际上是一种寻找wTz（即Y=wTz）wTz（即Y=wTz）的非高斯最大的不动点迭代方案。

以上有较多的数学推导，这里就省略了，下面给出fastICA的算法流程：

1. 观测数据的中心化
2. 数据白化
3. 选择需要估计的分量个数m，设置迭代次数和范围
4. 随机选择初始权重
5. 选择非线性函数
6. 迭代
7. 判断收敛，是下一步，否则返回步骤6
8. 返回近似混合矩阵的逆矩阵

TSNE降维

t-SNE（TSNE）将数据点之间的相似度转换为概率。原始空间中的相似度由高斯联合概率表示，嵌入空间的相似度由“t分布”表示。

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

• SNE构建一个高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有较低的概率被选择。
• SNE在低维空间里在构建这些点的概率分布，使得这两个概率分布之间尽可能的相似。

t-SNE模型是非监督的降维，他跟kmeans等不同，他不能通过训练得到一些东西之后再用于其它数据（比如kmeans可以通过训练得到k个点，再用于其它数据集，而t-SNE只能单独的对数据做操作，也就是说他只有fit_transform，而没有fit操作）

尽管SNE提供了很好的可视化方法，但是他很难优化，而且存在”crowding problem”(拥挤问题)。后续中，Hinton等人又提出了t-SNE的方法。与SNE不同，主要如下:

• 使用对称版的SNE，简化梯度公式
• 低维空间下，使用t分布替代高斯分布表达两点之间的相似度