关于推荐系统冷启动中的Bandit算法

推荐系统中经常会遇到EE问题和冷启动问题，Bandit算法就是为解决这两个问题的一种在线学习算法。

啥是EE问题

EE问题： 又称为exploit-explore问题。

exploit就是用户确定比较感兴趣的事物，要求准确率较高。

explore就是探索用户可能感兴趣的，新的事物。

因为只对用户感兴趣的事物进行推荐，用户很快会腻，我们需要科学的冒险的为用户推荐一些新鲜事物。

Bandit算法源于赌博学，一个赌徒去摇one-arm bandit，一个one-arm bandit共有 n 个外表一模一样的臂，每个臂的中奖概率为 Pi，他不知道每个臂中奖的概率分布，那么每次选择哪个臂可以做到收益最大化呢？这就是多臂赌博机 ( Multi-armed Bandit，MAB ) 问题。最好的办法就是去试一试，不是盲目的去试，而是有策略的快速的去试。这些策略，就是bandit算法。

bandit解决冷启动的大致思路如下：

我们用分类或者topic来表示用户兴趣，也就是MAB问题中的臂，我们可以通过几次实验，来刻画出新用户心目中对每个topic的感兴趣概率。
如果用户对某个topic感兴趣（提供了显示或者隐式反馈），就表示我们获得了收益；

如果推荐了不感兴趣的topic(也提供了显示或者隐式反馈，即用户明确反馈不感兴趣，或者用户对topic长时间，多次未进行任何操作，无动于衷)，推荐系统就表示regret了。
当一个用户来了， 针对这个用户，我们采用汤普森采样为每一个topic 采样一个随机数，排序后，我们取前top n的推荐item，注意，这里有一点改动，那就是在原始的多臂问题一次只摇一个臂，我们这里一次摇n个臂。
获取用户的反馈，比如点击。没有反馈则更新对应top的lose，点击了则更新对应topic的win值。

bandit 算法需要量化一个核心问题：错误的选择到底有多大的遗憾？如何使遗憾少一些？对同样的多臂问题，用不同的 bandit 算法试验相同次数，看看谁的 regret 增长得慢，以此衡量不同 bandit 算法在解决多臂问题上的效果。

常用的bandit算法

1 汤姆森采样（Thompson sampling） 算法

汤姆森采样是一种通过贝叶斯后验采样 ( Bayesian Posterior Sampling ) 进行探索与利用的方法。采用贝叶斯思想，对奖赏分布的参数假设一个先验分布，根据观测到的奖赏更新后验分布，根据后验分布选择臂。

在多臂one-arm bandit中,Bernoulli分布正好有Beta分布作为共轭先验,有了共轭先验,就容易做贝叶斯更新(根据证据来更新参数).

准确来说,多臂one-arm bandit问题中,每次选出推荐的物品(要拉的one-arm bandit)后,根据物品是否被转化(one-arm bandit是否吐出钱)来更新Beta分布的参数.有了新参数的Beta分布就是结合了这次经验后,被选中的物品(one-arm bandit)被转化率的更准确的估计.

而使用汤普森采样,允许我们利用每个物品被转化率的先验知识来设定每个beta分布的参数.

对应于多臂one-arm bandit的情景,一个物品(或one-arm bandit)的beta参数的

• α为一个物品被转化的次数加一,
• β为该物品被选中但没转化的次数加一.

如果我们在试验前就知道某个物品的被转化率为0.25,方差大概是0.00186,那么我们就可以得到先验α=25，β=75.然后每次抽到该物品后,被转化则α加1,否则β加1.

对于臂的奖赏服从伯努利分布，中奖概率 ( 被点击的概率 ) 即平均奖赏 θ_k∈[0,1]。假设第 k 个臂的奖赏分布固定但未知，即参数 θ_k 未知。在 Bernoulli Bandit 问题中，采用 Beta 分布对第 k 个臂的中奖概率建模，因为 Beta 分布是二项分布的共轭分布。如果先验分布为 Beta(α,β)，在观测到伯努力二元选择 ( Bernoulli Trial ) 后，后验分布变为 Beta(α+1,β) 或 Beta(α,β+1)。

• 如果候选物品被选中的次数很多，那么 Beta 分布随着 α_k+β_k 的增大会变得更加集中，即这个候选物品的收益已经确定，用它产生的随机数基本在分布的中心位置附近，且接近这个分布的平均收益。
• 如果一个候选物品的 α+β 很大，且 α/(α+β) 也很大，那么该候选物品是一个好的候选项，其平均收益也很好。
• 如果一个候选物品的 α+β 很小，且分布很宽，即没有给予充分的探索次数，无法确定好坏，那么这个较宽的分布有可能得到一个较大的随机数，在排序时被优先输出，并用给予次数进行探索。

在推荐的场景下，将beta分布的α参数作为曝光后用户的点击次数，β参数作为曝光未点击次数，汤姆森采样过程则为：

1. 取出每一个候选item对应的参数α和β；
2. 为每个候选item选用α和β作为参数，用beta分布产生一个随机数；
3. 按照随机数排序，输出最大值对应的候选；
4. 贯彻用户反馈，如果用户点击则将对应候选item的α+1，否则β+1；

相比于UCB算法，Thompson sampling：

• UCB采用确定的选择策略，可能导致每次返回结果相同（不是推荐想要的），Thompson Sampling则是随机化策略。
• Thompson sampling实现相对更简单，UCB计算量更大（可能需要离线/异步计算）
• 在计算机广告、文章推荐领域，效果与UCB不相上下或更好competitive to or better
• 对于数据延迟反馈、批量数据反馈更加稳健robust

补充概念

共轭先验

一个随机变量Χ服从参数为θ₁的分布,X_i~Dist₁(θ₁),而θ₁~Dist₂(θ₂).当我们根据Χ的抽样得到了证据,用证据和θ₁的先验分布计算出θ₁后验分布。

根据贝叶斯公式,

有posterior∝prior*evidence。其中

1. posterior=P(θ₁;X_i)叫做后验概率,它是有了样本后对先验的修正.
2. prior=P(θ₁)叫做θ₁先验概率.
3. evidence=P(X_i;θ₁)叫做证据,也是Likelihood(X_i;θ₁)抽样的似然概率.
4. ∝表示proportional to,等比例于。可以看到posterior∝prior*evidence符号两侧差了个P(X_i)倍数.

如果θ₁后验分布也是Dist₂,那么我们就说Dist₂是Dist₁的共轭先验。共轭先验分布在很多机器学习的问题中都提供了推断和参数估计的便利。

Beta分布

Beta分布像是为Bernoulli分布和二项式分布量身定做的共轭先验,是定义域(0, 1)上的随机变量的一种分布.它有两个大于0的参数,α,β.

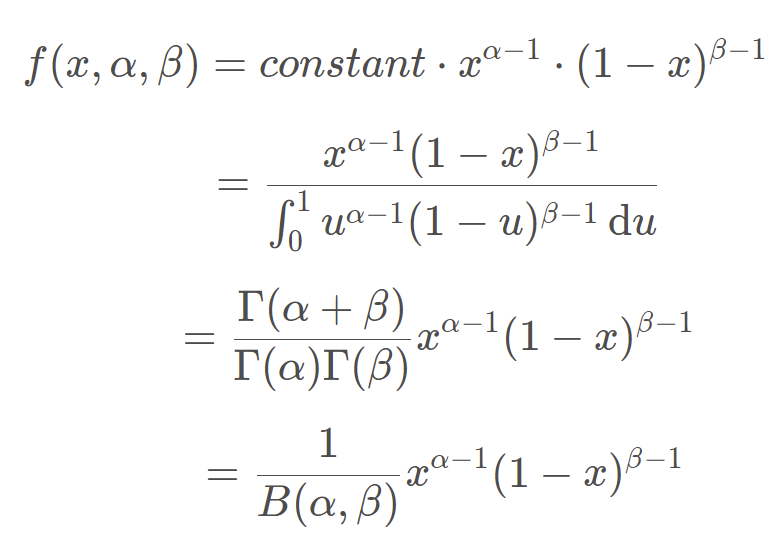
Beta分布的均值是：α/α + β

Beta分布的方差是：α*β/[(α+β)²(α+β+1)]

Beta分布图像：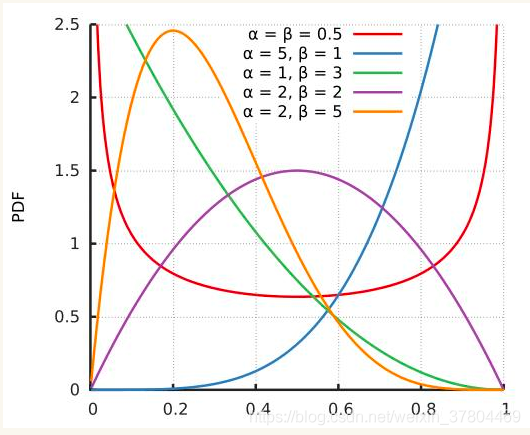

 

 举例来说，抛硬币n=α+β次，出现正面α次，反面β次时，P(x;α,β) ：表示【硬币出现正面的概率为x】的概率， 虽说这里叫概率，其实并不严谨，因为 P(x;α,β)的值并不在0～1之间，而是满足在【x: 0～1】，对 P(x;α,β)的积分等于1

当抛硬币4次，出现正面2次，反面2次，也就是图中紫色的那条线，那么单次抛硬币为正面的概率为x=0.5的概率（可能性）最大，为 P(x;α,β)=1.5； x=0.2的概率（可能性）只有 P(x;α,β)=1。而且在【x: 0～1】，对P(x;α,β)的积分等于1

 

 贴一个讲Beta分布的文章参考：https://zhuanlan.zhihu.com/p/33348118?ivk_sa=1024320u

举个栗子，在棒球里可以把击球当做随机事件，只有击中和没击中两种状态，衡量棒球运动员职业技能的一个指标就是棒球击球率（运动员击中的球数／总击球数），一般认为职业棒球运动员的击球率在0.25-0.3之间，如果击球率能达到0.3以上就可以认为是非常优秀的运动员了。

我们现在希望预测某棒球运动员在新赛季中的击球率。你可以直接以新赛季的击中数／击球数来估计，但这会有一个问题，如果现在是新赛季第一场，他就出场一次就被三振出局了，那他的击球率就是０％了？这显然不合理，合理的估计运动的击球率，需要考虑他的历史信息，如上赛季的击球率，这就是先验信息，而这个先验符合贝塔分布：

其中  是归一化函数，保证曲线下的面积总是１， p是参数，在这里就是棒球击球率。

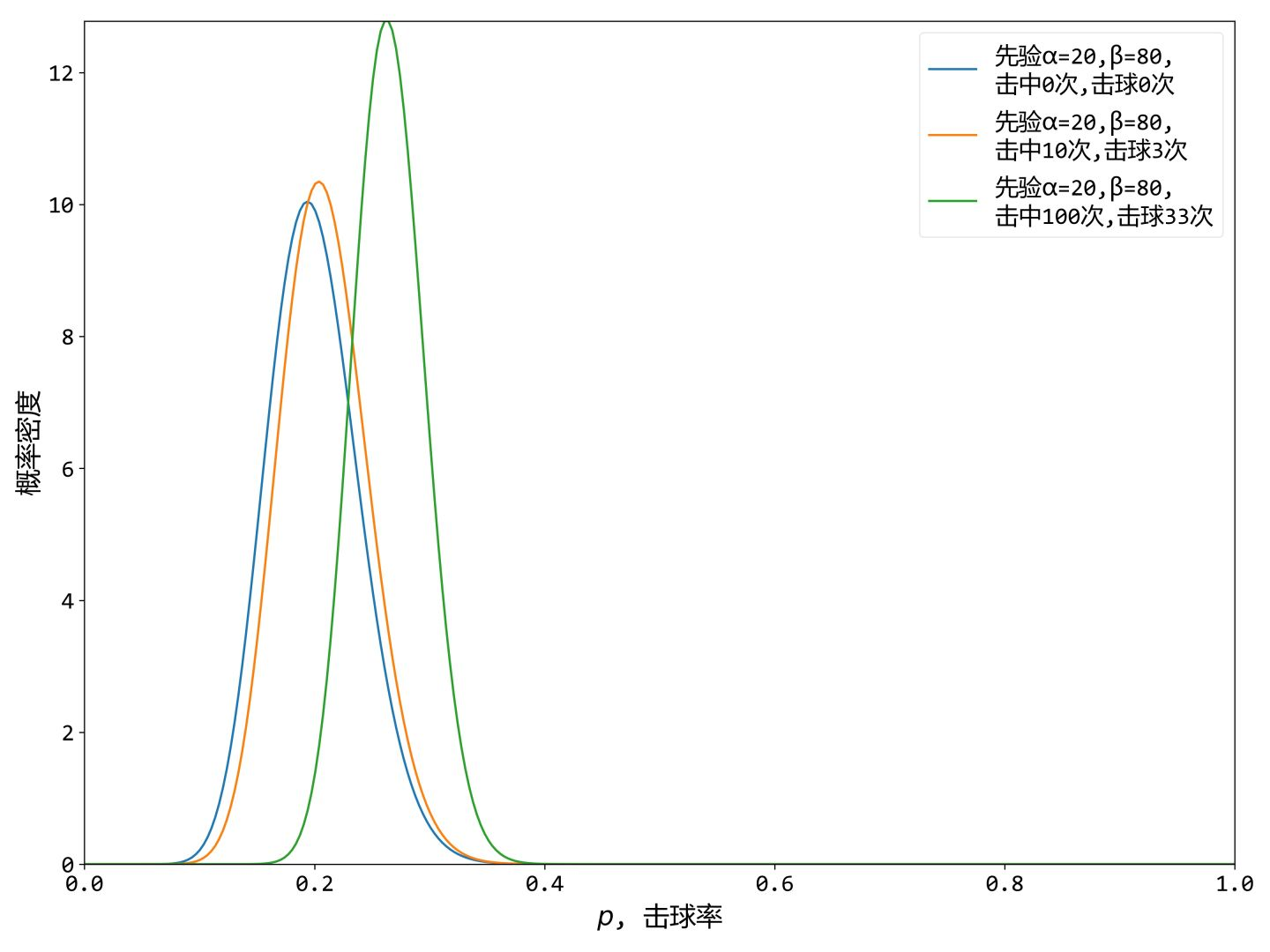
我们可以查到该运动员上赛季，共击球100次，其中击中20次，没击中80次。这样我们就有了贝塔分布的参数 ,如下图蓝色曲线，这就是击球率的贝塔先验。

我们可以根据参数  来估计一下：

• 先验贝塔分布的均值:
• 从图中可以看到先验贝塔分布主要在(0.１,0.3)之间，这是从历史数据中总结出的合理估计。

有了先验分布之后，我们来考虑一个运动员在新赛季击球10次，击中３次。这时候我们可以根据新观察的数据来更新分布，让曲线移动一些来适应我的新信息。贝塔分布与二项分布是共轭先验的。共轭先验的意思就是说如果先验分布是贝塔分布，那么其贝叶斯后验分布也是贝塔分布，所以此时新的后验贝塔分布就是：

其中 是先验分布的参数。在10击球后，  增加了3(击中3次)。  增加7(未击中7次)。这时候新的贝塔分布就是  ，如图中的橙色曲线。

可以看到新分布其实没多大变化，这是因为只打了10次球并不能说明什么问题。但如果我们得到了更多的数据，假设一共打了100次，击中了33次，未击中67次，那么这一新分布就是  ,如图绿色曲线所示。

可以看到绿色曲线，变得更尖了，并且向右平移了一段距离，表示该运动员的击球率提高了。

我们可以根据这个新的贝塔分布，估计出新的数学期望：

这比直接计算  要小。因为我们用了上赛季他击中20次，未击中80次这一先验信息。

2 UCB 算法

UCB 算法全称是 Upper Confidence Bound（置信区间上界）。

算法步骤：先对每一个臂都试一遍，之后在任意时刻  按照如下公式计算每个臂的分数，然后选择分数最大的臂作为选择

观察选择结果，更新t和T_j,k。其中  表示的是这个臂到目前的收益均值，j∈{1,……,K}，后面的叫做bonus，本质上是均值的标准差，t是目前的试验次数，T_j,k是这个臂被试次数。这个公式反映一个特点：均值越大，标准差越小，被选中的概率会越来越大，同时那些被选次数较少的臂也会得到试验机会。

 UCB思想是乐观地面对不确定性，以item回报的置信上限作为回报预估值的一类算法，其基本思想是：我们对某个item尝试的次数越多，对该item回报估计的置信区间越窄、估计的不确定性降低，那些均值更大的item倾向于被多次选择，这是算法保守的部分（exploitation）；对某个item的尝试次数越少，置信区间越宽，不确定性较高，置信区间较宽的item倾向于被多次选择，这是算法激进的部分（exploration）。

 

3 Epsilon-Greedy 算法

这个算法有点类似模拟退火的思想。选一个（0,1）之间较小的数ε ，每次以ε的概率在所有臂中随机选一个。以1-ε的概率选择截止当前，平均收益最大的那个臂。根据选择臂的回报值来对回报期望进行更新。这里ε的值可以控制对exploit和explore的偏好程度，每次决策以概率ε去Exploration，1-ε的概率来 Exploitation 。

这样做的好处在于：

• 能够应对变化：如果item的回报发生变化，能及时改变策略，避免卡在次优状态
• 可以控制对Exploration和Exploitation的偏好程度：ε大，模型具有更大的灵活性（能更快的探索潜在可能高回报item，适应变化，收敛速度更快），ε小，模型具有更好的稳定性（更多的机会用来开发利用当前最好回报的item），收敛速度变慢

虽然ε-Greedy算法在Exploration和Exploitation之间做出了一定平衡，但

• 设置最好的ε比较困难，大则适应变化较快，但长期累积回报低，小则适应变好的能力不够，但能获取更好的长期回报。
• 策略运行一段时间后，我们对item的好坏了解的确定性增强，但仍然花费固定的精力去exploration，浪费本应该更多进行exploitation机会
• 策略运行一段时间后，我们已经对各item有了一定程度了解，但没用利用这些信息，仍然不做任何区分地随机exploration（会选择到明显较差的item）

4 朴素bandit算法

先试若干次，然后计算每个臂的平均收益，一直选择均值最大的那个。

 

除了 bandit 算法之外，还有一些其他的 explore 的办法，比如：在推荐时，随机地去掉一些用户历史行为（特征）。解决 Explore，势必就是要冒险，势必要走向未知，而这显然就是会伤害用户体验的：明知道用户肯定喜欢 A，你还偏偏以某个小概率给推荐非 A。