LDA模型用来推测文档的主题分布，将文档集中每篇文档的主题以概率的形式给出，最终可以根据主题分布来对文档进行聚类或分类
LDA 采用词袋模型。所谓词袋模型，是将一篇文档，我们仅考虑一个词汇是否出现，而不考虑其出现的顺序。在词袋模型中，“我喜欢你”和“你喜欢我”是等价的。与词袋模型相反的一个模型是n-gram，n-gram考虑了词汇出现的先后顺序。
认为主题可以由一个词汇分布来表示，而文章可以由主题分布来表示。
比如有两个主题，美食和美妆。LDA说两个主题可以由词汇分布表示，他们分别是：
{面包：0.4，火锅：0.5，眉笔：0.03，腮红：0.07}
{眉笔：0.4，腮红：0.5，面包：0.03，火锅：0.07}同样，对于两篇文章，LDA认为文章可以由主题分布这么表示：
《美妆日记》{美妆：0.8，美食：0.1，其他：0.1}
《美食探索》{美食：0.8，美妆：0.1，其他：0.1}
LDA模型会涉及到大量概率论方面知识，包括二项分布，gamma函数，多项式分布，Beta分布，狄利克雷分布，Gibbs抽样，EM算法等。
二项分布
多项式分布
Gamma函数
beta分布
"""对于参数\alpha > 0, \beta > 0, 取值范围为[0, 1]的随机变量x的概率密度函数为"""
其中，
狄利克雷分布
其中，
beta分布和dirichlet分布均满足一个性质 对于beta分布，均值可以表示为α/(α/β) 对于dirichlet分布也类似
共轭分布
在贝叶斯概率理论中，如果后验概率P(Θ|x)和先验概率P(Θ)满足同样的分布律，那么先验分布和后验分布满足共轭分布
其中，beta分布是二项分布的共轭先验分布，狄利克雷分布是多项式分布的共轭先验分布
以二项分布和beta分布来说，如果数据满足二项分布，那么参数的先验分布和后验分布都能保持beta分布的形式，这样就能在先验分布中赋予参数明确的物理意义，并且可以延续到后验分布中进行解释。
LDA 训练的过程：
- 1. 对语料库中的每篇文档中的每个词汇ω，随机的赋予一个topic编号z
- 2. 重新扫描语料库，对每个词ω，使用Gibbs Sampling公式对其采样，求出它的topic，在语料中更新
- 3. 重复步骤2，直到Gibbs Sampling收敛
- 4. 统计语料库的topic-word共现频率矩阵，该矩阵就是LDA的模型；
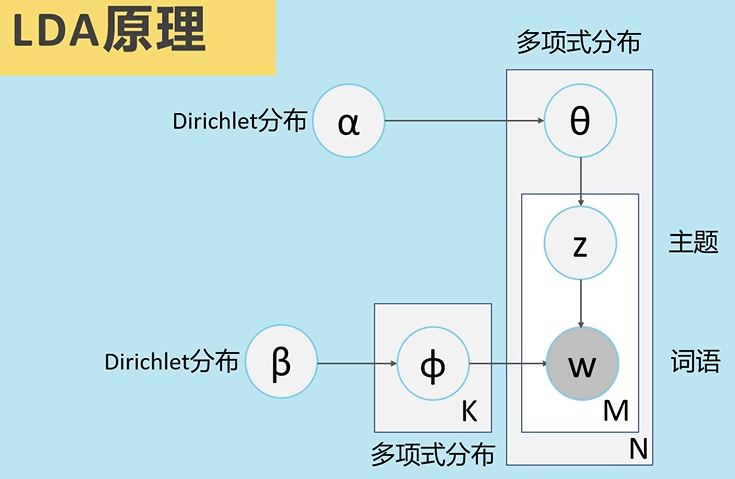
LDA 中，生成文档的过程如下：
- 1. 按照先验概率p(di)选择一篇文档di
- 2. 从Dirichlet分布α中取样生成文档di的主题多项式分布θi，主题分布θi由超参数为α的Dirichlet分布生成
- 3. 从主题的多项式分布θi中取样生成文档di第 j 个词的主题zi,j
- 4. 从Dirichlet分布β中取样生成主题zi,j对应的词语分布Φzi,j，词语分布Φzi,j由参数为β的Dirichlet分布生成
- 5. 从词语的多项式分布Φzi,j以及zi,j中采样最终生成词语ωi,j
循环，生成一个文档的m个词语，最终生成k个主题下的n个文档
主题划分的衡量
主题困惑度：为对于一篇文章d，所训练出来的模型对文档d属于哪个主题有多不确定，这个不确定成都就是困惑度。困惑度越低，说明聚类的效果越好。最小困惑度所对应的Topic就是最优的主题数
分母是测试集中所有单词之和，即测试集的总长度，不用排重。其中p(w)指的是测试集中每个单词出现的概率，计算公式如下
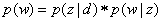
p(z|d)表示的是一个文档中每个主题出现的概率，p(w|z)表示的是词典中的每一个单词在某个主题下出现的概率
