二分法排序

    二分法排序其实是一种改进的插入排序，也是通过查找待插入位置来实现排序，这和插入排序是类似的。

    算法思想，在插入第i个元素时，对前面的0～i-1元素进行折半，先跟他们中间的那个元素比，如果小，则对前半部分再进行折半，否则对后半进行折半，

直到left<right，然后再把第i个元素前1位与目标位置之间的所有元素后移，再把第i个元素放在目标位置上。

    二分法实际上没有进行排序，只进行了有查找。所以当找到要插入的位置时，必须从移动最后一个记录开始，向后移动一位，再移动倒数第2位，直到要插入的位置的记录移后一位。

    下面的图展示了二分法排序的工作原理，看图

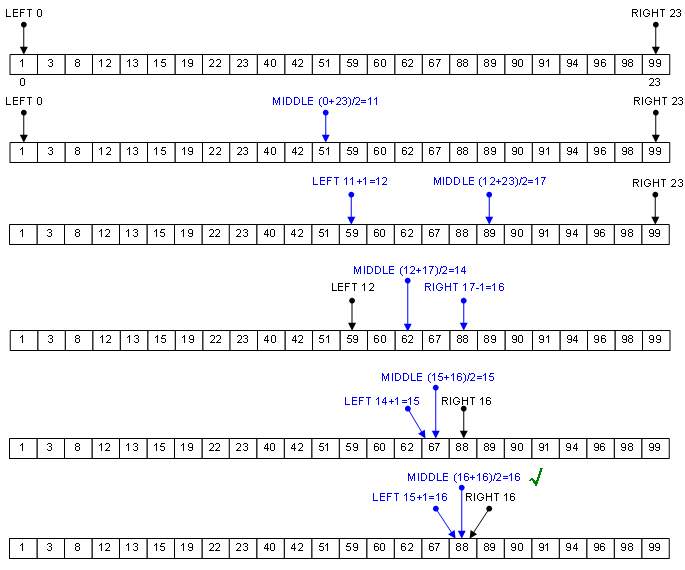
    下面通过代码来实现二分法排序，上代码

#include<iostream>
using namespace std;

void dichotomizingsort(int a[],int n)  //升序排列
{
   int i,j,mid=0,left,right,tem=0;
   for(i=1;i<n;i++)
   {
       tem=a[i];
       left=0;  //指向有序表的低位
       right=i-1;   //指向有序表的高位
       while(left<=right)  //当left和right向中间靠拢的时候发生碰撞就结束排序
       {
          mid=(left+right)/2;  //取有序表中间的那一个元素
          if(a[mid]>tem)   
                    right=mid-1; //待插入元素比大中间元素小，就对前半部分再折半    
          else
                    left=mid+1;  //待插入元素不小于中间元素，就对后半部分再折半 
        }
       for(j=i-1;j>=left;j--)  //left就是在有序表中待插入的位置，但要先把left之后的所有元素向后移动一位
       {
            a[j+1]=a[j];
       }
       a[left]=tem;  //移动后就可以插入了
       cout<<"第"<<i<<"次待插入的数据是："<<tem<<endl;
       cout<<"此时有序表中的数据位：";
       for(j=0;j<=i;j++)
           cout<<a[j]<<" ";
       cout<<endl;
   }
}  
int main()
{
    int a[10]={34,4,78,35,3,64,45,18,26,35};
    dichotomizingsort(a,10);
    cout<<"执行插入排序后数组为：";
    for(int i=0;i<10;i++)
        cout<<a[i]<<" ";
    return 0;
}

测试结果如下：

 

最后来说一下复杂度

空间复杂度：和插入排序一样，只用到了一个辅助空间，为O(1)。

时间复杂度：二分法排序是一种稳定的排序算法，与二分排序的复杂度相同；最好的情况是当插入的位置刚好是二分位置 所用时间为O(log2n)；最坏的情况是当插入的位置不在

二分位置， 所需比较次数为O(n)，无限逼近线性查找的复杂度；而平均时间复杂度为O(n^2)。

     本人水平有限，如有错误欢迎指出 ！谢谢！

 

      2020-04-30      18:03:11