北航软工项目作业（一）

博客三

项目	内容
这个作业属于哪个课程	2020春季计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	第一次项目作业
我在这个课程的目标	不求变强，只求做好，成为一颗有用的螺丝钉。
这个作业在哪个具体方面帮助我实现目标	使用单元测试以及性能分析工具
参考资料
教学班级	005
项目地址	链接

PSP

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	5	5
· Estimate	· 估计这个任务需要多少时间	5	0
Development	开发	345	690
· Analysis	· 需求分析 (包括学习新技术)	0	180
· Design Spec	· 生成设计文档	0	0
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	0	0
· Design	· 具体设计	15	60
· Coding	· 具体编码	30	30
· Code Review	· 代码复审	120	120
· Test	· 测试（自我测试，修改代码，提交修改）	180	300
Reporting	报告	60	45
· Test Report	· 测试报告	25	10
· Size Measurement	· 计算工作量	15	15
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	20	20
	合计	450	775

思路描述

考虑最暴力的方法，两两直线求交点，那么时间复杂度是$O(n^2)$，这个时间复杂度肯定是不可以接受的。

那么有更好的办法吗？除了如果不存在平行和三线共点，那么交点数应该是$n(n-1)/2$。如果新增的一条线与$x$条直线平行，那么会少$x$个交点；如果新增的一条直线与l另外$x(x>2)$条直线共点，那么会少$x$个交点。欲求得平行条件不难，时间复杂度为$O(1)$；欲求共点条件还是会用上遍历，这里的时间开销又回到了$O(n^2)$。

所以，我放弃了，规规矩矩地使用暴力方法，选择了两点式求直线交点，再去百度上找轮子。

设计实现过程

大体的思路是先计算，再把计算结果保存在集合中，由于集合不存在重复的元素，所以对于本次作业来说是一个比较好的数据结构，需要重写比较函数。

相比于求取斜率的截距式，两点式更加安全，但是计算效率会更低（截距式2个参数，两点式4个参数）。

首先就是构造Dot类和重写比较函数。然后构造一个 set<Dots, DotsCmp>类。

计算交点的函数的介绍放在关键代码部分。

再将这些函数封装起来。

Dots类：

class Dots {
public:
    double DotX;
    double DotY;
    Dots() {
        DotX = 0;
        DotY = 0;
    }
    Dots(double X, double Y) {
        DotX = X;
        DotY = Y;
    }
};

重写比较函数:

class DotsCmp {
public:
    bool operator()(const Dots& dotA, const Dots& dotB) const {
        if (dotA.DotX == dotB.DotX) {
            return (dotA.DotY < dotB.DotY);
        }
        else {
            return (dotA.DotX < dotB.DotX);
        }
    }
};

计算结果的类：

class CalDots {
private:
    DotsSet _set;//交点集合
public:
    CalDots();
    Dots CalDot(int x0, int y0, int x1, int y1, int x2, int y2, int x3, int y3);//计算两直线交点
    int DotsSize();//返回总交点数
};

单元测试1——CalDot()函数的正确性

TEST_METHOD(TestCalDot)
		{
			CalDots*cald = new CalDots();
			int x0 = 0;
			int y0 = 0;
			int x1 = 1;
			int y1 = 1;
			int x2 = 0;
			int y2 = 0;
			int x3 = 0;
			int y3 = 0;
			double dotx = 0;
			double doty = 0;
			Assert::AreEqual(dotx, cald->CalDot(x0, y0, x1, y1, x2, y2, x3, y3).DotX);
			Assert::AreEqual(doty, cald->CalDot(x0, y0, x1, y1, x2, y2, x3, y3).DotY);
		}

单元测试2——时间

TEST_METHOD(TestTime)
		{
			srand(time(NULL));
			long t = clock();
			CalDots* cald = new CalDots();
			int Dot[5000][4];
			int i, j;
			for (i = 0; i < 5000; i++) {
				Dot[i][0] = rand() % 1000;
				Dot[i][1] = rand() % 1000;
				Dot[i][2] = rand() % 1000;
				Dot[i][3] = rand() % 1000;
			}

			for (i = 0; i < 5000; i++) {
				for (j = i + 1; j < 4999; j++) {
					cald->CalDot(Dot[i][0], Dot[i][1], Dot[i][2], Dot[i][3], Dot[j][0], Dot[j][1], Dot[j][2], Dot[j][3]);
				}
			}
			Assert::IsTrue(clock() - t < 60000);
		}

实测5000条直线耗时54秒，效率很低，大部分用在set排序上。

时间记录及改进思路

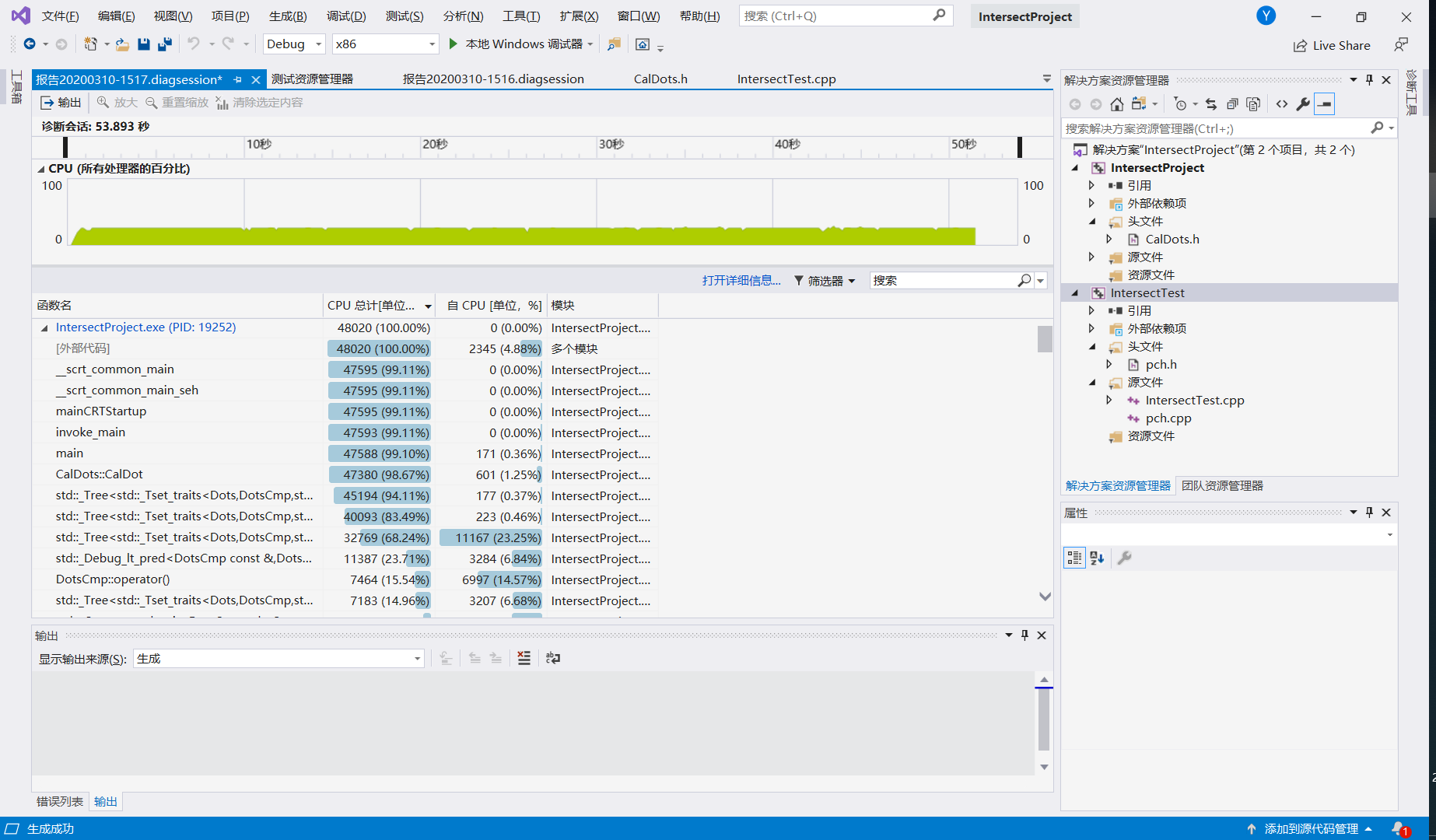
耗时最大的函数是CalDot()函数（关键代码部分），即计算两直线交点的函数；而其中耗时最多的是将计算得到的点插入set集合中。这一工作是内置函数完成的，暂时想不到改进策略。可以改善的是简化计算步骤，将两点式转换为截距式，但截距式存在k不存在的情况，不仅会增加程序的错误处理，而且对速度提升不大。

关键代码

Dots CalDots::CalDot(int x0, int y0, int x1, int y1, int x2, int y2, int x3, int y3) {
    double k1, k2;
    if (x0 != x1) {
        k1 = (y0 - y1) / (x0 - x1);//if x0 == x1  k1 do not exist
        if (x2 != x3) {
            k2 = (y2 - y3) / (x2 - x3);
            if (k1 != k2) {
                DotX = (k1 * x0 - k2 * x2 + y2 - y0) / (k1 - k2);
                DotY = y0 + (DotX - x0) * k1;
                _set.insert(Dots(DotX, DotY));
                return Dots(DotX, DotY);
            }
            //else paralle
        }
        else {
            DotX = x2;
            DotY = y0 + ((double)x2 - (double)x0) * k1;
            _set.insert(Dots(DotX, DotY));
            return Dots(DotX, DotY);
        }
    }
    else {
        if (x2 != x3) {
            k2 = (y2 - y3) / (x2 - x3);//k2 exists
            DotX = x0;
            DotY = y2 + ((double)x0 - (double)x2) * k2;
            _set.insert(Dots(DotX, DotY));
            return Dots(DotX, DotY);
        }
        //else paralle
    }
    return Dots(DotX, DotY);
}