北航软工个人项目作业
个人项目作业-求图形交点个数
| 项目 | 内容 |
|---|---|
| 本作业属于北航 2020 年春软件工程 | 博客园班级连接 |
| 本作业是本课程个人项目作业 | 作业要求 |
| 我在这个课程的目标是 | 收获团队项目开发经验,提高自己的软件开发水平 |
| 这个作业在哪个具体方面帮助我实现目标 | 体验软件开发的 Workflow |
| 项目代码 | Github 仓库 |
解题思路
根据需求描述,我们不难得到所需软件的运行流程,总体而言分为三步:
- 解析命令行参数,获取输入文件与输出文件的路径
- 从输入文件中获取输入,并对图形参数进行解析,存储于相应的数据结构中
- 求解图形之间的交点个数,并输出
第一步是命令行交互软件的基本操作,不再赘述。
第二步的关键在于设计存储图形所需的数据结构。考虑图形有两种:直线与圆,且直线的输入数据是两点式,圆的输入数据是圆心-半径式,同时点需要两个参数来标识,半径需要一个参数来标识,因此每个点用数对来存储,每条直线用两个点来表示,每个圆用一个点和一个半径来表示。
第三步是最复杂的。图形类型有两种,因此有\(C^2_3\)种情况需要纳入考虑范围内。根据数学知识,继续划分如下:
- 直线与直线
- 平行:交点个数 0
- 同一条直线:交点个数无限
- 相交:交点个数 1
- 直线与圆
- 相离:交点个数 0
- 相切:交点个数 1
- 相交:交点个数 2
- 圆与圆
- 相离:交点个数 0
- 相切:交点个数 1
- 相交:交点个数 2
- 内含:交点个数 0
每一种情况都有完整的初等解法,参见 Paul Bourke 先生的文章。
设计
数据结构
同上述提到的数据结构设计。CPP 代码如下
using Point = std::pair<int32_t, int32_t>;
using Line = std::pair<Point, Point>;
using Circle = std::pair<Point, float>;
对于交点的存储,如果只有直线,那么可以用两个整数来表示有理数的方法实现,不存在精度的问题。但是除了直线以外还有圆,引入了无理数,因此浮点数是有必要的。CPP 代码如下。
struct IntersectPoint
{
float first;
float second;
IntersectPoint(float first, float second) : first(first), second(second) {}
bool operator < (const IntersectPoint& rhs) const
{
return first - rhs.first < -eps || (!(rhs.first - first < -eps) && second - rhs.second < -eps);
}
friend bool operator < (IntersectPoint& left, IntersectPoint& right)
{
return left.operator<(right);
}
};
可以发现,我没有选择使用 STL 内建数据结构,而是使用自定义类,原因在于精度。由于浮点数的不准确性,两个数学上相等的值在计算机中可能会因为运算的原因产生误差,此时需要使其在一定程度上容许误差的存在,因此不能容许误差的 STL 内建数据结构不是一个好的选择。
复杂度分析
对于需求中的第三步操作,我的策略如下:每个图形都与其他图形计算一次交点,存储交点并去重。不难发现,时间复杂度与空间复杂度均为\(\Theta(n^2)\)。
实际上,这个复杂度是难以接受的,尤其是对于 50W 的输入数据量而言。在测试时,空间占用更是一度达到了 32GB。由于时间关系,我暂且还未找到更佳的处理策略。
代码实现
代码组织
共有 5 个主要文件,其中 main.cpp 与 option.hpp 主要内容是用户交互与 benchmark,intersect.cpp 与 intersect.hpp 主要内容是主要功能的实现,intersect_test.cpp 的内容则是测试相关。
IntersectProject
└── src
├── main.cpp
├── intersect.cpp
└── include
├── intersect.hpp
├── option.hpp
└── test
└── intersect_test.cpp
在 intersect.cpp 中,函数的关系大致如下
calculate_intersect_points - 计算图形之间的交点个数
├── calculate_line_circle_intersect_points - 计算一条直线和一个圆之间的交点个数
├── calculate_line_intersect_points - 计算两条直线之间的交点个数
└── calculate_circle_intersect_points - 计算两个圆之间的交点个数
可以看出,只要功能函数的组织和需求分析是相吻合的。
不同情况下的返回值处理
正如上面提到的,两个图形在不同的位置有着不同的相对关系,从而影响着交点的个数。
但总的来说,分为两种,0 个和 2 个(相切时,交点相同)。这种情况下,我选择 C++17 引入的 std::optional,这是一个 Sum Type,可以优雅地处理不同返回值问题,不需要额外引入 flag 变量以标志返回值内容。
测试
对于两个图形位置的每个可能情况,都有相应的一个测试点。代码覆盖率如下:

(使用 OpenCPPCoverage 生成,由于测试问题,与用户交互的 main.cpp 和 option.hpp 基本没有覆盖,只覆盖了功能实现的 intersect.cpp)
代码质量分析
如下

实际上,我的 Visual Studio 是配以 Jetbrains 的 Resharper C++ 使用的,Resharper C++ 可以帮助我调用 clang-tidy 及时地对代码风格与质量进行提醒。
性能改进
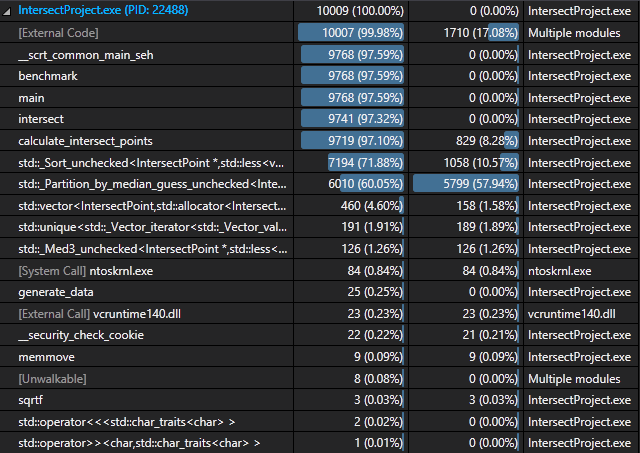
初始时,我选择 std::set 作为交点的存储容器。经过 profile 之后,我发现热点在于 set::insert,它的调用次数非常多,而且每次调用的花销非常高。因此,我选择了 std::vector 作为容器,在处理完毕后再进行排序去重操作。对于 1000 级别的数据量而言,性能提高了约三倍。但是,目前的性能热点仍然在于排序去重操作,这是我目前采取的处理策略所不能避免的。
事后总结
由于本次任务的需求是确定的,没有太多需要揣测的地方,因此需求分析花费的时间比较少。
而本次任务花费时间最多的阶段是设计阶段,主要在于寻找一个不需要复杂运算且具有足够精度的方法。在数学上,可以使用反三角函数来轻松解决这个问题,但是在计算机中,反三角函数是一个复杂的运算过程,且精度一般。我尝试使用 Mathmatica 辅助求解,但给出的计算公式十分复杂,没能充分利用图形本身的特征进行简化。最后,我找到了 Paul Bourke 先生的文章,方法很简洁,计算过程也适合于计算机。
PSP 表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 5 | 5 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 15 | 15 |
| · Design Spec | · 生成设计文档 | 10 | 10 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 0 | 0 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 0 | 0 |
| · Design | · 具体设计 | 30 | 90 |
| · Coding | · 具体编码 | 60 | 60 |
| · Code Review | · 代码复审 | 10 | 10 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 60 | 60 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 10 | 10 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 30 |
| 合计 | 240 | 300 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号