51nod1265判断四点共面
给出三维空间上的四个点(点与点的位置均不相同),判断这4个点是否在同一个平面内(4点共线也算共面)。如果共面,输出"Yes",否则输出"No"。
Input
第1行:一个数T,表示输入的测试数量(1 <= T <= 1000) 第2 - 4T + 1行:每行4行表示一组数据,每行3个数,x, y, z, 表示该点的位置坐标(-1000 <= x, y, z <= 1000)。
Output
输出共T行,如果共面输出"Yes",否则输出"No"。
Input示例
1 1 2 0 2 3 0 4 0 0 0 0 0
Output示例
Yes
题意:中文题
思路:判断四点是否共面问题,点乘和叉乘的应用,任意向量到某一三角形平面的法向量垂直,则四点共面;
还有一种思路是利用行列式:
若行列式为0,则共面;否则不共面。
下面只给出第一种思路的代码:
#include<iostream>
#include<stdio.h>
using namespace std;
typedef long long ll;
struct point
{
double x, y, z;
point operator - (point &o)
{
point ans;
ans.x = this->x - o.x;
ans.y = this->y - o.y;
ans.z = this->z - o.z;
return ans;
}
};
double dot_product(const point &a, const point &b)
{
return a.x * b.x + a.y * b.y + a.z * b.z;
}
point cross_product(const point &a, const point &b)
{
point ans;
ans.x = a.y * b.z - a.z * b.y;
ans.y = a.z * b.x - a.x * b.z;
ans.z = a.x * b.y - a.y * b.x;
return ans;
}
int main()
{
point p[4];
int T;
for (scanf("%d", &T); T--;)
{
for (int i = 0; i < 4; ++i)
{
scanf("%lf%lf%lf", &p[i].x, &p[i].y, &p[i].z);
}
puts(dot_product(p[3] - p[0], cross_product(p[2] - p[0], p[1] - p[0])) == 0.0 ? "Yes\n" : "No\n");
}
return 0;
}

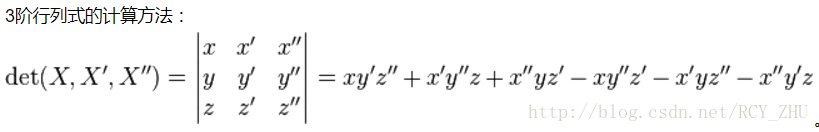

 浙公网安备 33010602011771号
浙公网安备 33010602011771号