51nod 1135 原根
设m是正整数,a是整数,若a模m的阶等于φ(m),则称a为模m的一个原根。(其中φ(m)表示m的欧拉函数)
给出1个质数P,找出P最小的原根。
Input
输入1个质数P(3 <= P <= 10^9)
Output
输出P最小的原根。
Input示例
3
Output示例
2
1.原根定义:设m>1,gcd(a,m)=1,使得![这里写图片描述]() 成立的最小的r,称为a对模m的阶。
成立的最小的r,称为a对模m的阶。
 成立的最小的r,称为a对模m的阶。
成立的最小的r,称为a对模m的阶。 2.定理:如果模m有原根,那么他一共有![这里写图片描述]() 个原根。这里的函数表示[1,m)中与m互质的个数
个原根。这里的函数表示[1,m)中与m互质的个数
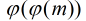 个原根。这里的函数表示[1,m)中与m互质的个数
个原根。这里的函数表示[1,m)中与m互质的个数3.定理:如果p为素数,那么素数p一定存在原根,并且模p的原根的个数为![这里写图片描述]() 个。
个。
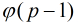 个。
个。4.定理:假设m是正整数,a是整数,如果a模m的阶等于![这里写图片描述]() ,则称a为模m的一个原根。
,则称a为模m的一个原根。
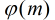 ,则称a为模m的一个原根。
,则称a为模m的一个原根。5.模m有原根的充要条件:m=2,4,P^a,2*P^a…….
求模素数P的原根的方法:对P-1素因子分解,即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。,若恒有![这里写图片描述]() 成立,那么g就是P的原根(对于合数而言,只需要把p-1换成
成立,那么g就是P的原根(对于合数而言,只需要把p-1换成![这里写图片描述]() 即可)
即可)
求模素数P的原根的方法:对P-1素因子分解,即P-1=(P1^a1)(P2^a2)…..(Pk^ak)。,若恒有
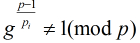 成立,那么g就是P的原根(对于合数而言,只需要把p-1换成
成立,那么g就是P的原根(对于合数而言,只需要把p-1换成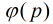 即可)
即可)#include <stdio.h>
#include <math.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <sstream>
#include <algorithm>
#include <set>
#include <queue>
#include <stack>
#include <map>
#include <bitset>
#pragma comment(linker, "/STACK:102400000,102400000")
using namespace std;
typedef long long LL;
const int inf=0x3f3f3f3f;
const double pi= acos(-1.0);
const double esp=1e-7;
const int Maxn=1e6+10;
int prime[Maxn];//存储素数
int sprime[Maxn];//存储P-1的素因子
bitset<Maxn>pri;//结果只有0和1,判断是否为素数
int k;//记录Maxn以内的素数个数
int cnt;//记录素因子的个数
void is_prime()
{
pri.set();//将所有的二进制数都标为1
for(int i=2; i<Maxn; i++) {
if(pri[i]) {
prime[k++]=i;
for(int j=i+i; j<Maxn; j+=i)
pri[j]=0;
}
}
}
void Divide(int n)//将n分解为素因子
{
cnt=0;
int t=(int)sqrt(1.0*n);
for(int i=0; prime[i]<=t; i++) {
if(n%prime[i]==0) {
sprime[cnt++]=prime[i];
while(n%prime[i]==0)//因为有可能有多个peime[i]
n/=prime[i];
}
}
if(n>1)
sprime[cnt++]=n;//可能只有自己一个素因子
}
LL modexp(LL a,LL b,int mod)//快速幂取余
{
LL res=1;
while(b>0) {
a=a%mod;
if(b&1)
res=res*a%mod;
b=b>>1;
a=a*a%mod;
}
return res;
}
int main()
{
int p;
is_prime();
while(~scanf("%d",&p)) {
Divide(p-1);
for(int g=2; g<p; g++) {
int flag=1;
for(int i=0; i<cnt; i++) {
int t=(p-1)/sprime[i];
if(modexp(g,t,p)==1) {
flag=0;
break;
}
}
if(flag) {
int root=g;
printf("%d\n",root);
break;//去掉break的话是求所有的原根,加上break是求最小的原根、
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号