洛谷P3960 列队

题目描述

Sylvia 是一个热爱学习的女孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有n×m名学生，方阵的行数为 n，列数为 m。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 1 到 n×m 编上了号码（参见后面的样例）。即：初始时，第 i 行第 j 列 的学生的编号是(i−1)×m+j。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)描述，表示第 x 行第 y 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：

1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 x 行第 m列。

2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 n 行第 m列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行 第 m 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：

 

输入共 q+1 行。

第 1 行包含 3 个用空格分隔的正整数 n,m,q，表示方阵大小是 n 行 m 列，一共发 生了 q 次事件。

接下来 qq 行按照事件发生顺序描述了 q 件事件。每一行是两个整数 x,y，用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 x 行第 y 列。

 

输出格式：

 

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学 生的编号。

 

输入输出样例

输入样例#1： 复制

2 2 3 
1 1 
2 2 
1 2 

输出样例#1： 复制

1
1
4

说明

【输入输出样例 1 说明】

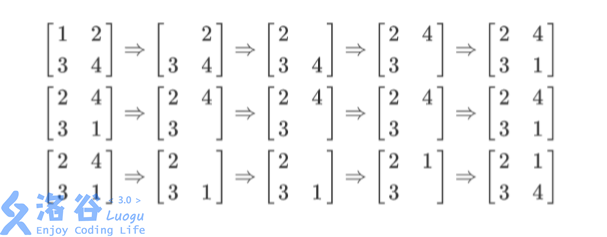
列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为1 的同学离队，这时空位在第一行第一列。接着所有同学 向左标齐，这时编号为 2的同学向左移动一步，空位移动到第一行第二列。然后所有同 学向上标齐，这时编号为4的同学向上一步，这时空位移动到第二行第二列。最后编号 为1 的同学返回填补到空位中。

【数据规模与约定】

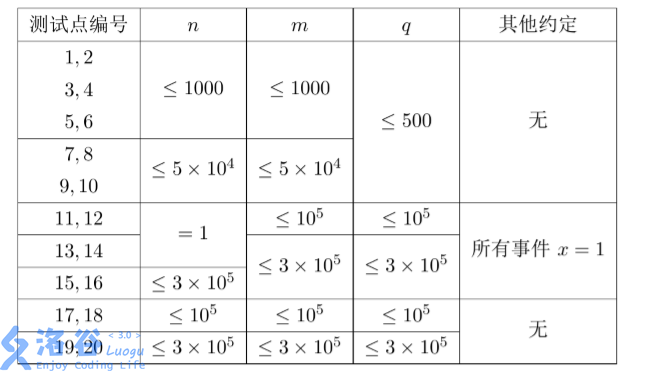
数据保证每一个事件满足 1≤x≤n,1≤y≤m

/*
    其实这道题目昨天就已经A了 但是今天才写 可能考前写题解rp++吧
    这题是去年NOIP2017的D2T3压轴题，难度还是有，就是要仔细思考和细致推理。
    这道题其实有很多种解法，据说标程是树状数组，然后平衡树啥的也有人写。
    不过我是个蒟蒻什么都不会，于是就只会搞搞动态加点线段树了（也是临时学的）
    考虑到离队时有变化的事当前行的点，当前行的最后一点和当前列的最后一点
    考虑对每一行建一个维护前m-1个节点的线段树，再给最后一列建一个线段树 总共n+1棵
    但是每一行（或之后一列）需要的大小最多为mx = max(m,n)+q
    但是如果建普通的线段树的话，空间会达到O(nm)，肯定会爆空间。
    于是我们使用一个叫做动态加点线段树 只维护已经修改的节点，这样的话空间会降很多，在可容纳范围内。
    然后我们考虑加进来的人怎么办。同样的，给每一行和最后一列维护一个vector，就存后来加进来的人。
    一行后来加进来的肯定是最后一列这一行的那个人，最后一列加进来的人就是之前走了的这个人。
    于是这题就做完了辣。一些细节写在了程序当中。
*/

#include <bits/stdc++.h>
#define ll long long
using namespace std;

const int maxn = 300005;

int ls[maxn*20],rs[maxn*20],rt[maxn*20],size[maxn*20];//分别存的是当前点的左儿子、右儿子、根节点、节点的大小
int n,m,q,mx,cnt,ans;

vector<ll> G[maxn];//求每一行以及最后一列后来加进来的人

void change(int &o,int l,int r,int x){//找到要找的这个点
    if(!o) o = ++cnt;//如果这个点还没有开，那就开呗
    size[o]++;//这是个使用标记 表示区间o使用了多少次
    if(l == r) return ;
    int mid = (l+r) >> 1;
    if(x <= mid) change(ls[o],l,mid,x);
    else change(rs[o],mid+1,r,x);//注意范围
}

int kth(int o,int l,int r,int x){//查询第x个数的位置 
    if(l == r) return l;
    int mid = (l+r) >> 1;
    int lsz = (mid-l+1) - size[ls[o]];//lsz表示的左儿子还没有开的点的大小
    if(x <= lsz)  ans = kth(ls[o],l,mid,x);//如果x在左儿子里，那就进左儿子
    else  ans = kth(rs[o],mid+1,r,x - lsz);//在右儿子里就进右儿子
    return ans;
}

ll query_lie(int x){
    int pos = kth(rt[n+1],1,mx,x);//找到要离开当前位置的这个人
    change(rt[n+1],1,mx,pos);//离队操作
    if(pos > n) return G[n+1][pos-n-1];//如果这个人是后来才加进来的
    else return 1ll * pos * m;//这个人本来就在队中
}

ll query_hang(int x,int y){
    int pos = kth(rt[x],1,mx,y);//找到要离开当前位置的这个人
    change(rt[x],1,mx,pos);//离队操作
    if(pos >= m) return G[x][pos-m];//如果这个人是后来才加进来的
    else return 1ll * (x-1) * m + pos;//这个人本来就在队中
}

int main(){
    int x,y;
    scanf("%d%d%d",&n,&m,&q);
    mx = max(n,m)+q;
    for(int i = 1;i <= q;i++){
        scanf("%d%d",&x,&y);
        if(y == m){//特判一下最后一列的情况
            ll res = query_lie(x);//找到这个人
            G[n+1].push_back(res);//在最后一列又加回去
            printf("%lld\n",res);
        }else{
            ll res = query_hang(x,y);//出走的这个人
            ll res2 = query_lie(x);//最后一列会往前补的这个人
            G[n+1].push_back(res);//这个人归队
            G[x].push_back(res2);//加到第x行后面
            printf("%lld\n",res);
        }
    }
    return 0;
}