图像的空间域(spatial domain)主要指组成图像的像素点集合。spatial domain process是对空间像素点的直接操作。如果用公式描述为:
\( g(x,y) = T{\left[f(x,y)\right]} \)
\(f(x,y)\)是输入图像,\(g(x,y)\)是输出图像,空域处理在输入图像上定义了一种操作得到输出图像,往往这种操作对像素点处理,针对像素点\((x,y)\)及其8邻域像素点的操作处理。也可以仅对像素点\((x,y)\)操作,此时\(T\)称为gray-level transformingation function,灰度变换函数。
\(s = T(r)\)
常用的灰度变换函数:
log transformation对数变换,函数形式
\(s = clog(1 + r)\)
根据函数得到函数图像:

Power-Law transformation指数变换,函数形式:
\(s = cr^\gamma\),
函数图像:

对数变换和指数变换都可以将较小范围的灰度值映射到较大的灰度值区间,也可以将很大的灰度值区间映射到较小的灰度区间,可以提高对比度。一般在得到图像的傅立叶频谱图后,频谱图像会处在很大的灰度区间,需要对此作对数或指数变换,图像可视效果会更好。
还有对比度拉伸变换,函数形式:
\(s = \frac{1}{1+(\frac{m}{r})^E} \),
输出图像的灰度值被限制在[0,1]内,该变换函数以m为阈值,灰度值低于m的被削弱,高于m的被增强,指数E控制了削弱域增强的度,从图像上看为曲线的陡峭程度。E越大越陡;

以上三种变换在matlab中都可以用函数 imadjust实现。
g = imadjust(f,[low_in,high_in],[low_out,high_out],gamma) 定义了指定输入输出区间上的指数变换,设定不同的gamma值有不同的映射曲线。
以下是MATLAB对图像做指数变换,目的是增强一定区域内的灰度显示效果。
1 >> f = imread('D:\MATLAB\image\DIP3E_Original_Images_CH03\Fig0308(a)(fractured_spine).tif'); 2 >> ff = mat2gray(f); 3 >> g1 = imadjust(ff,[],[],0.6); 4 >> g2 = imadjust(ff,[],[],0.4); 5 >> g3 = imadjust(ff,[],[],0.3); 6 >> subplot(2,2,1); 7 >> imshow(f); 8 >> g1 = im2uint8(g1); 9 >> g2 = im2uint8(g2); 10 >> g3 = im2uint8(g3); 11 >> subplot(2,2,2); 12 >> imshow(g1); 13 >> subplot(2,2,3); 14 >> imshow(g2); 15 >> subplot(2,2,4); 16 >> imshow(g3);
效果图:

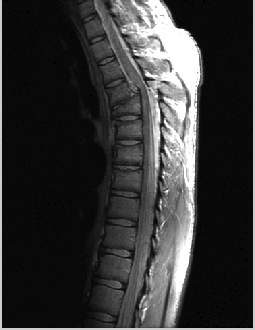


最左边是源图像,从做到右依次使用了gamma值为0.6,0.4,0.3的指数变换,指数图像是上凸形状。拉伸了较暗区域的灰度显示空间,但对明亮区域的变化不大。最终结果是能够发现原图较暗区域被覆盖的内容。
1 >> f = imread('D:\MATLAB\image\DIP3E_Original_Images_CH03\Fig0309(a)(washed_out_aerial_image).tif'); 2 >> ff = mat2gray(f); 3 >> g1 = imadjust(ff,[],[],3); 4 >> g2 = imadjust(ff,[],[],4); 5 >> g3 = imadjust(ff,[],[],5); 6 >> subplot(2,2,1); 7 >> imshow(f); 8 >> g1 = im2uint8(g1); 9 >> g2 = im2uint8(g2); 10 >> g3 = im2uint8(g3); 11 >> subplot(2,2,2); 12 >> imshow(g1); 13 >> subplot(2,2,3); 14 >> imshow(g2); 15 >> subplot(2,2,4); 16 >> imshow(g3);
效果图:




最左边是原图,是一张washed-out的图像,曝光率过大,使用gamma值为3,4,5的指数变换,压缩了明亮区域的灰度空间,但只对较暗区域做微调,较好的还原了图像。但个人认为,指数变换,或灰度变换都是在灰度或亮度级的变换,能够增强明暗显示效果,但无法提高分辨率。但明暗显示效果增强可以给边缘检测和图像分割带来很大的益处。
另外MATLAB下对比度拉伸变换和对数变换可以直接使用函数形式:
g = im2uint8(mat2gray(log(1+double(f))));
g = 1 ./ (1+(m./(double(f)+eps)).^E)
opencv下可以使用函数cvLUT来实现灰度变换。
一个简单的例子,opencv程序 指数变换:
1 #include "cv.h" 2 #include "highgui.h" 3 #include <math.h> 4 #define GAMMA 5 5 /* 6 指数变换测试:s = c*pow(r,gamma) 7 */ 8 9 int main(int argc,char**argv) 10 { 11 IplImage * img; 12 if(argc ==2 && (img = cvLoadImage(argv[1],0))!=0) 13 { 14 IplImage *dist = cvCreateImage(cvSize(img->width,img->height),IPL_DEPTH_8U,1); 15 CvMat *lu_mat = cvCreateMatHeader(1,256,CV_8UC1); 16 uchar lu[256]; 17 float f = 0.0f; 18 int d = 0; 19 for(int i =0;i<256;i++) 20 { 21 f = (float)i/255; 22 d = pow(f,GAMMA)*255; 23 lu[i] = d; 24 } 25 cvSetData(lu_mat,lu,0); 26 cvLUT(img,dist,lu_mat); 27 cvNamedWindow("origin",CV_WINDOW_AUTOSIZE); 28 cvNamedWindow("convert",CV_WINDOW_AUTOSIZE); 29 cvShowImage("origin",img); 30 cvShowImage("convert",dist); 31 cvWaitKey(0); 32 cvReleaseImage(&img); 33 cvReleaseImage(&dist); 34 cvDestroyWindow("origin"); 35 cvDestroyWindow("convert"); 36 } 37 }
效果图:

Gonzalez在他的Digital Image Processing中提到了另外几个灰度空间变换的技巧,其实,总结一下,对数,指数等基于函数的灰度空间变换,正如OpenCv中cvLUT的实现一样,是从已经定义好的映射规则中查询每个point的映射,映射规则体现了函数的形式,因为像素和像素点本就离散,所以对函数的连续与平滑没有严格要求,只要能将每一个point映射到合适的值即可。Gray-level-slicing是一个分段函数的映射规则,用于增强指定灰度区间的灰度值,有两种形式,函数图像如下:

另外,还提到了一个比较有趣的基于point的灰度空间处理,Bit-plane-slicing,不基于函数,而是基于每个point的比特位,如果8位灰度图像,每个像素点有8位二进制值表示其灰度值大小,可以将8位从高到低分成8个等级,每个等级对应一位,所有像素点的同一等级就组成了一个平面,称为一个bit-plane,例如对于最高位,如果是1,就将其灰度值映射到255,如果为0,映射到0;每个bit-plane就是一个二值图像,共有8个bit-plane,每个plane代表了不同的信息,高位可能体现了较大的轮廓,而低位可能体现了更多的细节。
以下是Bit-plane-slicing的opencv实现:
1 #include "cv.h" 2 #include "highgui.h" 3 #include <math.h> 4 5 int main(int argc,char ** argv) 6 { 7 IplImage *src = 0; 8 if(argc == 2 && (src = cvLoadImage(argv[1],0))!=0) 9 { 10 IplImage * dist[8]; 11 for(int i = 0;i<8;i++) 12 { 13 dist[i] = cvCreateImage(cvSize(src->width,src->height),IPL_DEPTH_8U,1); 14 } 15 uchar data = 0x01; 16 for(int i = 0;i<8;i++) 17 { 18 cvAndS(src,cvScalar(data),dist[i]); 19 cvDiv(NULL,dist[i],dist[i],pow(2,(float)i)); 20 cvCvtScale(dist[i],dist[i],255,0); 21 data = data << 1; 22 } 23 cvNamedWindow("origin",CV_WINDOW_AUTOSIZE); 24 cvShowImage("origin",src); 25 cvNamedWindow("bitone",CV_WINDOW_AUTOSIZE); 26 cvShowImage("bitone",dist[0]); 27 cvNamedWindow("bittwo",CV_WINDOW_AUTOSIZE); 28 cvShowImage("bittwo",dist[1]); 29 cvNamedWindow("bitthr",CV_WINDOW_AUTOSIZE); 30 cvShowImage("bitthr",dist[2]); 31 cvNamedWindow("bitfour",CV_WINDOW_AUTOSIZE); 32 cvShowImage("bitfour",dist[3]); 33 cvNamedWindow("bitfive",CV_WINDOW_AUTOSIZE); 34 cvShowImage("bitfive",dist[4]); 35 cvNamedWindow("bitsix",CV_WINDOW_AUTOSIZE); 36 cvShowImage("bitsix",dist[5]); 37 cvNamedWindow("bitseven",CV_WINDOW_AUTOSIZE); 38 cvShowImage("bitseven",dist[6]); 39 cvNamedWindow("biteight",CV_WINDOW_AUTOSIZE); 40 cvShowImage("biteight",dist[7]); 41 cvWaitKey(0); 42 cvReleaseImage(&dist[0]); 43 cvReleaseImage(&dist[1]); 44 cvReleaseImage(&dist[2]); 45 cvReleaseImage(&dist[3]); 46 cvReleaseImage(&dist[4]); 47 cvReleaseImage(&dist[5]); 48 cvReleaseImage(&dist[6]); 49 cvReleaseImage(&dist[7]); 50 cvReleaseImage(&src); 51 cvDestroyWindow("bitone"); 52 cvDestroyWindow("bitwo"); 53 cvDestroyWindow("bithr"); 54 cvDestroyWindow("bitfour"); 55 cvDestroyWindow("bitfive"); 56 cvDestroyWindow("bitsix"); 57 cvDestroyWindow("bitseven"); 58 cvDestroyWindow("biteight"); 59 cvDestroyWindow("origin"); 60 } 61 62 }
效果图:








第一幅为原图,接下来是从高位到低位的bit-plane平面图。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号