UVa - 1025 - A Spy in the Metro

Secret agent Maria was sent to Algorithms City to carry out an especially dangerous mission. After several thrilling events we find her in the first station of Algorithms City Metro, examining the time table. The Algorithms City Metro consists of a single line with trains running both ways, so its time table is not complicated.

Maria has an appointment with a local spy at the last station of Algorithms City Metro. Maria knows that a powerful organization is after her. She also knows that while waiting at a station, she is at great risk of being caught. To hide in a running train is much safer, so she decides to stay in running trains as much as possible, even if this means traveling backward and forward. Maria needs to know a schedule with minimal waiting time at the stations that gets her to the last station in time for her appointment. You must write a program that finds the total waiting time in a best schedule for Maria.

The Algorithms City Metro system has N stations, consecutively numbered from 1 to N. Trains move in both directions: from the first station to the last station and from the last station back to the first station. The time required for a train to travel between two consecutive stations is fixed since all trains move at the same speed. Trains make a very short stop at each station, which you can ignore for simplicity. Since she is a very fast agent, Maria can always change trains at a station even if the trains involved stop in that station at the same time.

Input 

The input file contains several test cases. Each test case consists of seven lines with information as follows.

Line 1.

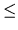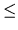The integer N ( 2N50), which is the number of stations.

Line 2.

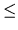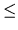The integer T ( 0T200), which is the time of the appointment.

Line 3.

N - 1 integers: t₁, t₂,..., t_{N - 1} ( 1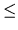t_i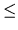70), representing the travel times for the trains between two consecutive stations: t₁ represents the travel time between the first two stations, t₂ the time between the second and the third station, and so on.

Line 4.

The integer M1 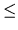( 1M1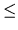50), representing the number of trains departing from the first station.

Line 5.

M1 integers: d₁, d₂,..., d_M1 ( 0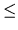d_i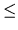250 and d_i < d_{i + 1}), representing the times at which trains depart from the first station.

Line 6.

The integer M2 ( 1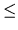M2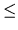50), representing the number of trains departing from the N-th station.

Line 7.

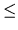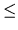M2 integers: e₁, e₂,..., e_M2 ( 0e_i250 and e_i < e_{i + 1}) representing the times at which trains depart from the N-th station.

The last case is followed by a line containing a single zero.

Output 

For each test case, print a line containing the case number (starting with 1) and an integer representing the total waiting time in the stations for a best schedule, or the word `impossible' in case Maria is unable to make the appointment. Use the format of the sample output.

Sample Input 

4
55
5 10 15
4
0 5 10 20
4
0 5 10 15
4
18
1 2 3
5
0 3 6 10 12
6
0 3 5 7 12 15
2
30
20
1
20
7
1 3 5 7 11 13 17
0

Sample Output 

Case Number 1: 5
Case Number 2: 0
Case Number 3: impossible

动态规划，注意状态函数的定义就可以。其它技巧还有不须要把t，d，e所有存下来。仅仅须要输入的时候顺便计算出一个状态数组hasTrain就可以。

时间复杂度是O(nT)。

AC代码：

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cctype>
#include <cstring>
#include <string>
#include <sstream>
#include <vector>
#include <set>
#include <map>
#include <algorithm>
#include <stack>
#include <queue>
#include <bitset> 
#include <cassert> 
#include <cmath>
#include <functional>

using namespace std;

const int maxt = 75;
const int maxm = 55;
const int maxT = 205;
const int maxn = 55;
const int inf = 0x3f3f3f3f;

int n, T, M1, M2;
int t[maxt], d;
int dp[maxT][maxn]; // dp(i,j)表示时刻i。在车站j，最少还须要等待多长时间
int hasTrain[maxT][maxn][2];
// hasTrain[t][i][0]表示时刻t。在车站i是否有往右开的火车

void init()
{
	memset(t, 0, sizeof(t));
	memset(dp, 0, sizeof(dp));
	memset(hasTrain, 0, sizeof(hasTrain));
	cin >> T;
	for (int i = 1; i <= n - 1; i++) {
		cin >> t[i];
	}

	cin >> M1;
	for (int i = 1; i <= M1; i++) {
		cin >> d;
		for (int j = 1; j <= n - 1; j++) {
			if (d <= T) {
				hasTrain[d][j][0] = 1;
			}
			d += t[j];
		}
	}

	cin >> M2;
	for (int i = 1; i <= M2; i++) {
		cin >> d;
		for (int j = n - 1; j >= 1; j--) {
			if (d <= T) {
				hasTrain[d][j + 1][1] = 1;
			}
			d += t[j];
		}
	}
}

// 动态规划求解
void solve()
{
	for (int i = 1; i <= n - 1; i++) {
		dp[T][i] = inf;
	}
	dp[T][n] = 0;

	for (int i = T - 1; i >= 0; i--) {
		for (int j = 1; j <= n; j++) {
			dp[i][j] = dp[i + 1][j] + 1;
			if (j < n && hasTrain[i][j][0] && i + t[j] <= T) {
				dp[i][j] = min(dp[i][j], dp[i + t[j]][j + 1]);
			}
			if (j > 1 && hasTrain[i][j][1] && i + t[j - 1] <= T) {
				dp[i][j] = min(dp[i][j], dp[i + t[j - 1]][j - 1]);
			}
		}
	}
}

int main()
{
	ios::sync_with_stdio(false);
	int kase = 0;
	while (cin >> n && n) {
		init();
		solve();
		cout << "Case Number " << ++kase << ": ";
		if (dp[0][1] >= inf) {
			cout << "impossible\n";
		}
		else {
			cout << dp[0][1] << "\n";
		}
	}

	return 0;
}