2016 百度之星 复赛 - 拍照

小明在旅游的路上看到了一条美丽的河，河上有许多船只，有的船只向左航行，有的船只向右航行。小明希望拍下这一美丽的风景，并且把尽可能多的船只都完整地拍到一张照片中。

小明位于河的边上，并且可以在河边的任意位置进行拍照，照相机的视野恰好为90度角，只能以垂直于河边的方向进行拍照。河上的船只全都可看作是平行于河边的一条线段，跟河边的距离各不相同，有的正在向左移动，有的正在向右移动，但移动速度恰好都是一样的。小明可以等待恰当的时间让尽量多的船只都走进照相机的视野里，你不需要考虑船只之间会互相遮挡视野的情况。

 

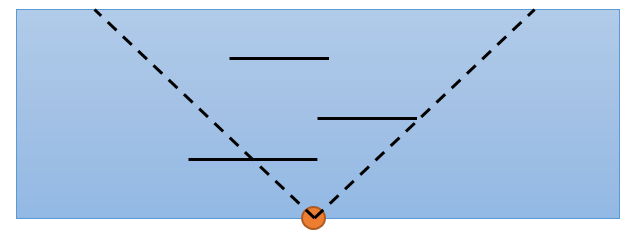
思路：

 

首先得发现这两条规律：

1.设船到河岸的距离为h，则如果 y-x > 2*h ，则这条船不可能被完整拍到。

2.设河岸[l,r]范围内能够拍到船，则 l=y-h , r =x+h 。

 

然后计算每个河岸上的点能够拍到多少条船，两个方向分别处理。

 

后面的真是不好叙述，如果当面用草稿纸说明会比较方便，看代码吧。数据范围太大，需要离散化。

 

#include "algorithm"
#include "iostream"
#include "cstring"
#include "cstdio"
#include "string"
#include "stack"
#include "cmath"
#include "queue"
#include "set"
#include "map"

#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1

typedef long long ll;
typedef unsigned long long ull;
using namespace std;

const int inf=0x3f3f3f3f;
const int maxn=1e6+5;
const int mod = 1e9 +7;

//从右开始顺时针
int dir4[4][2]= {0,1,1,0,0,-1,-1,0};
int dir8[8][2]= {0,1,1,1,1,0,1,-1,0,-1,-1,-1,-1,0,-1,1};

int n;


int lisan[maxn<<1];
int lsum[maxn<<1];
int rsum[maxn<<1];

struct Ship
{
    int x,y,h,d;
    int l,r;
    bool see()
    {
        return (y-x) <= (h<<1) ;
    }
} ship[10000+5];

int main()
{
    //freopen("in_3.txt","r",stdin);
    int t;
    scanf("%d",&t);
    for(int ii=1; ii<=t; ii++)
    {
        printf("Case #%d:\n",ii);

        memset(lsum,0,sizeof lsum);
        memset(rsum,0,sizeof rsum);

        scanf("%d",&n);
        int index = 0;

        for(int i=0; i<n; i++)
        {
            scanf("%d%d%d%d",&ship[i].x,&ship[i].y,&ship[i].h,&ship[i].d);
            if( !ship[i].see() )
            {
                //printf("cant see:%d\n",i);
                continue;
            }

            ship[i].l = ship[i].y-ship[i].h;
            ship[i].r = ship[i].x+ship[i].h;

            lisan[index++] = ship[i].l;
            lisan[index++] = ship[i].r;
        }

        sort(lisan,lisan+index);

        int mm=1;
        for(int i=1;i<index;++i)
        {
            if( lisan[i]!=lisan[i-1] )
            {
                lisan[mm++]=lisan[i];
            }
        }

        for(int i=0;i<n;++i)
        {
            if( !ship[i].see() )
            {
                //printf("cant see:%d\n",i);
                continue;
            }

            int l = lower_bound(lisan,lisan+mm,ship[i].l) - lisan;
            int r = lower_bound(lisan,lisan+mm,ship[i].r) - lisan;

            if( ship[i].d==1 ) //right
            {
                rsum[l] ++;
                rsum[r+1]--;
            }
            else
            {
                lsum[l] ++;
                lsum[r+1]--;
            }
        }

        for(int i=1 ;i<mm;++i)
        {
            rsum[i] +=rsum[i-1];
            lsum[i] +=lsum[i-1];
        }

        int rm = 0,ans=0;
        for(int i=0;i<mm;++i)
        {
            rm = max(rm,rsum[i]);
            ans = max(ans,rm+lsum[i]);
        }
        printf("%d\n",ans);
    }

    return 0;
}