三角函数的另外三个伙伴—cot，sec，csc
原文网址：https://zhuanlan.zhihu.com/p/162297688?utm_source=qq
二.知识讲解
1.认识另外三个小伙伴
首先说cot
我估计部分高中生应该学过cot。它叫余切，和tan互为倒数。所以，在直角三角形里，tan是对边/邻边，那cot自然是邻边/对边了
其次是sec，它叫正割
类似地，cos和sec互为倒数，直角三角形里是斜边/邻边
这里我多说一句，我建议大家学一下sec的读音，否则一说到它就叫s e c，这不方便叫
来想一个场景
老师说：同学们，s i n 30 得多少啊
注意啊，不是sin，是s i n
所以我觉得学学读音有必要啊
好啦第三个伙伴，是csc，叫余割，它和sin互为倒数，同样地这个也建议学一下读音，其它内容类比之前的即可
2.画图像
注意啊是画图，我觉得初学时应该自己探究着画。一方面，亲自动手和直接看图像肯定是不一样的；另一方面，这个过程一定程度上也锻炼了探究能力
引个路，咱们首先画y=secx，不妨拿起笔和纸，尝试一下
注意最开始可以找图像上的几个点（结合sec和cos互为倒数），然后像线绳串珠子一样，画出大致的图像
因为有现成的图，所以我就不画了啊，但初学时一定要自己画一遍
来看标准图和自己画的是否大致相同
如果把图放大，你会感觉y=secx的每个单元（也就是每半个周期）像啥？是不是有点像大铲子。。。。。。
由于在二.1中我们说过，cos和sec互为倒数，所以实际上，我们还可以借助cos的图像来得到y=secx
来把它们画在一块
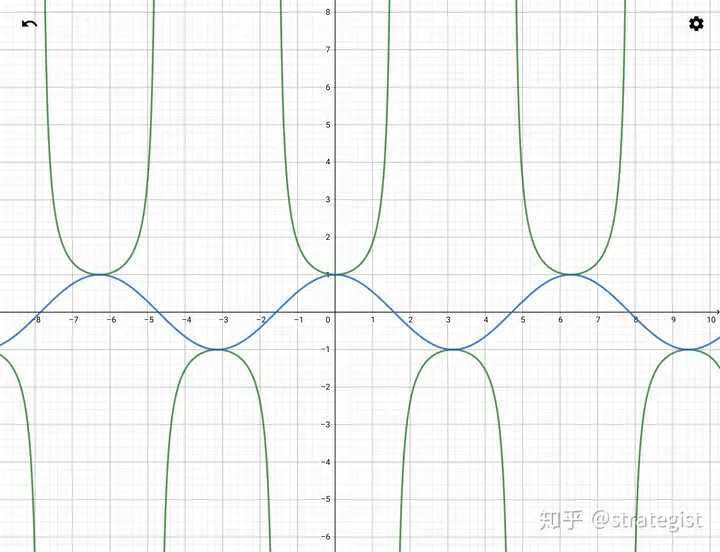
我觉得这么记住y=secx的图像是最好的
所以同样地，y=cscx的图像也是一样的研究方法
这里给出图像，其它的请读者按之前的思路进行
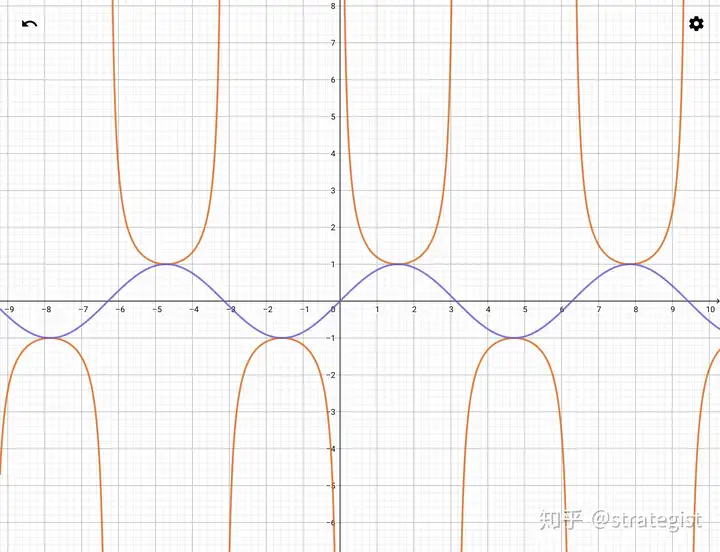
这里我强调一个点，就是周期性
由图3和图4可知，正割函数和余割函数都是以2pi为最小正周期的
但我们知道，正切函数的最小正周期是pi
所以若根据tan与cot互为倒数来演变画图像，我们可以知道y=cotx的最小正周期也为pi
当然画y=cotx也可以找特殊点再串线来画
探究过程请读者进行
这里同样直接给出图像
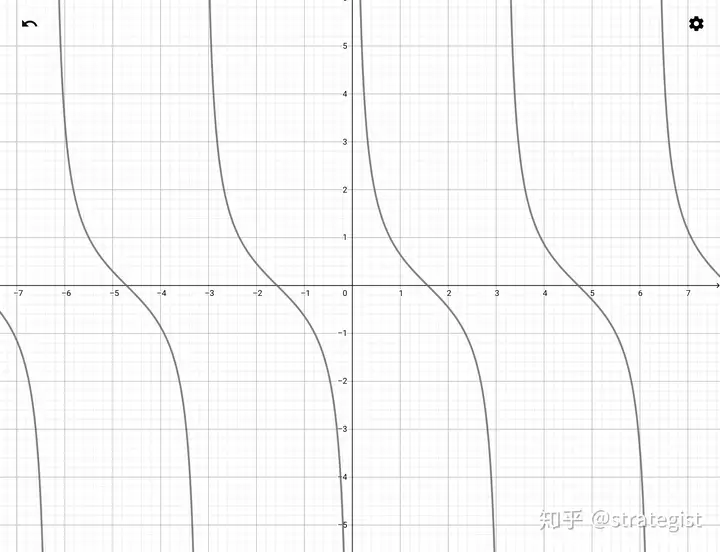
在画出图像后，请读者分别从函数的定义域、值域、周期性、奇偶性、单调性、对称性六个方面进行研究
3.六边形记忆法
这个方法我觉得真的很好，也借此来总结和添加相关公式
直接上图
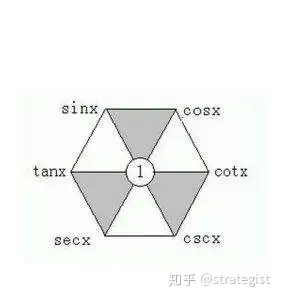
先来观察一下，看看能发现哪些规律
我们先从宏观角度来审视
纵向的看，六边形的左半都为“正”，右半都为“余”
类似地，横向的看，最上面一行为“弦”，中间一行为“切”，而最后一行为“割”
我一般喜欢简称为“正余弦切割”
也建议大家在画出这个六边形时，可以分别把这五个字标在图上，这样更清晰些
从微观角度看，主要可以得到3条规律
我喜欢叫它为“邻，间，对”
诶，大家有没有想到化学里的二甲苯？
反正我是这么类比着记的
来，首先看对位（比如tan和cot）
诶，这不就是我们最开始讲到的互为倒数吗？
没错
而且六边形里的三对都符合
这就是“对”的规律
其次呢，我们看“邻”
比如sin和cos
我们会看到六边形的中心有个1
所以我们会想到sin^2+cos^2=1
也正是最上面的阴影三角形
类似的，就有tan^2+1=sec^2，cot^2+1=csc^2
这个大家能联想到什么呢？
我想到的是杨辉三角
说白了，就是由两个肩上扛的数得到下面那个数
我觉得这么记比较好
最后一个是“间”的规律
也就是六边形每个顶点都等于与它相邻的两个函数的乘积
比如sec=tan*csc
ok，在已经能吃透六边形的内在规律后，我们再来把公式详细地摆出来
我想现在再来看这堆公式就不会觉得难记了
三.总结
本文主要讲了cot，sec，csc的图像和一些常用公式
