【笔记】机器学习的数学基础
1. 相似度的度量
L1范数: ||x||为x向量各个元素绝对值之和
L2范数: ||x||为x向量各个元素的平方和的开方。L2范数又称Euclidean范数或者Frobenius范数
Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方。
L∞范数: ||x||为x向量各个元素绝对值最大的元素,如下:
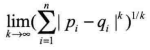
from numpy import *
A = [8,1,6]
modA = sqrt(sum(power(A,2))) # 手工计算
normA = linalg.norm(A) # numpy库函数
2. 距离的表示法
- 闵可夫斯基距离(Minkowski Distance)
- 欧式距离(Euclidean Distance)
- 曼哈顿距离(Manhattan Distance)
- 切比雪夫距离(Chebyshev Distance)
- 夹角余弦(Cosine)
- 汉明距离(Hamming Distance)
- 杰卡德相似系数(Jaccard Similiarity Coeffcient)
2.1. 闵可夫斯基距离(Minkowski Distance)
严格意义上讲,闵可夫斯基距离不是一种距离,而是一组距离的定义。
两个n维变量 A(x11,x12,...,x1n)与 B(x21,x22,...,x2n)间的闵可夫斯基距离定义为:
其中p是一个变参数:
- 当p=1时,就是曼哈顿距离
- 当p=2时,就是欧式距离
- 当p=∞时,就是切比雪夫距离
根据变参数的不同,闵可供夫斯基可以表示一类的距离。
2.2. 欧式距离(Euclidean Distance)
欧氏距离(L2范数)是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式
-
二维平面上两点 a(x1,y1)与 b(x2,y2)间的欧式距离
-
三维空间两点 A(x1,y1,z1)与 B(x2,y2,z2)
-
两个n维向量A(x11,x12,...,x1n)与B(x21,x22,...,x2n)间的欧氏距离
vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) nDist = sqrt((vector1-vector2)*((vector1-vector2).T))
2.3. 曼哈顿距离(Manhattan Distance)
-
二维平面两点 A(x1,y1) 与 B(x2,y2) 间的曼哈顿距离:
-
两个n维向量 A(x11,x12,...,x1n)与B(x21,x22,...,x2n)间的曼哈顿距离
vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) nDist = sum(abs(vector1-vector2))
2.4. 切比雪夫距离(Chebyshev Distance)

-
二维平面两点A(x1,y1)与B(x2,y2)间的切比雪夫距离
-
两个n维平面两点A(x11,y12,..,x1n)与B(x21,y22,..,x2n)间的切比雪夫距离
这个公式的另外一种等价形式是:
vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) nDist = abs(vector1-vector2).max()
2.5. 夹角余弦(Consine)
几何中的夹角余弦可用来衡量两个向量方向的差异。

-
二维平面两点A(x1,y1)与B(x2,y2)间的夹角余弦公式:
-
两个n维样本点A(x11,x12,x13,...,x1n)与B(x21,x22,...,x2n)的夹角余弦:
即:
夹角余弦取值范围为[-1,1]。夹角余弦越大,表示向量的夹角越小;夹角余弦越小,表示两个向量的夹角越大。当两个向量的方向重合时,夹角余弦取最大值1;当两个向量的方向完全相反时,夹角余弦取值最小值-1.
vector1 = mat([1,2,3]) vector2 = mat([4,5,6]) cosV12 = dot(vector1,vector2.T)/(linalg.norm(vector1)*linalg.norm(vector2))
2.6. 汉明距离(Hamming Distance)
汉明距离的定义:两个等长的字符串s1和s2之间的汉明距离定义为将其中一个变为另外一个所需要的最小替换次数。例如字符串“1111“与“1001”之间的汉明距离为2。
应用:信息编码(为了增强容错性,应使编码间的最小汉明距离尽可能大)。
matV = mat([[1,1,0,1,0,1,0,0,1], [0,1,1,0,0,0,1,1,1]])
'''
matrix([[1, 1, 0, 1, 0, 1, 0, 0, 1],
[0, 1, 1, 0, 0, 0, 1, 1, 1]])
'''
diffV = matV[0] - matV[1]
'''
matrix([[ 1, 0, -1, 1, 0, 1, -1, -1, 0]])
'''
smstr = nonzero(diffV)
'''
(array([0, 0, 0, 0, 0, 0], dtype=int64),
array([0, 2, 3, 5, 6, 7], dtype=int64))
'''
print( np.shape(smstr[0])[1] ) # output: 6
2.7. 杰卡德相似系数(Jaccard Similarity Coefficient)
-
杰卡德相似系数:两个集合A和B的交集元素在A、B的并集中所占的比例,成为两个集合的杰卡德相似系数,用符号J(A,B)表示。
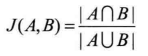
杰卡德相似系数是衡量两个集合的相似度的一种指标。
-
杰卡德距离:与杰卡德相似系数相反的概念是杰卡德距离(Jaccard Distance),杰卡德距离可用如下的公式表示:
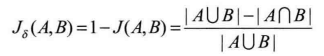
杰卡德距离用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度。
-
杰卡德相似系数与杰卡德距离的应用
可将杰卡德相似系数用在衡量样本的相似度上。
样本A与样本B是两个n维向量,而且所有维度上的取值都是0或者1.例如,A(0111)和 B(1011)。我们将样本看成一个集合,1表示该集合包含该元素,0表示集合不包含该元素。
- P:样本A与B都是1的维度的个数
- q:样本A是1、样本B是0的维度的个数
- r: 样本A是0、样本B是1的维度的个数
- s:样本A与B都是0的维度的个数
那么样本A与B的杰卡德相似系数可以表示为:
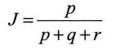
这里p+q+r可以理解为A与B的并集的元素个数,而p是A与B的交集的元素个数。
from numpy import * import scipy.spatial.distance as dist # 导入Scipy距离公式 matV = mat([[1,1,0,1,0,1,0,0,1],[0,1,1,0,0,0,1,1,1]]) print( dist.pdist(matV, 'jaccard') ) # output: [0.75]
3. 概率论
3.1. 理解随机性

如果从统计学的角度来看,蝴蝶效应说明了两方面的意义:一方面,样本总体(特征向量)的取值范围一般是确定的,所有样本对象(包括已经存在的和未出现的)的取值都位于此空间范围内;另一方面,无论收集再多的样本对象,也不能使这种随机性降低或者消失。因此,随机性是事物的一种根本的、内在的、无法根除的性质,也是一切事物(概率)的本质属性。
结论:随机性是隐藏在我们生活中最普遍的规律(而不是确定性!)
3.2. 贝叶斯公式
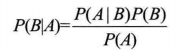
4. 特征间的相关性
样本数据一般以矩阵形式存在,行向量代表了某一个样本的形状(用于分类);而对于其特征向量,研究的是整个样本空间在某个特征列上的规律,其符合概率统计(用于预测)。
- 期望:衡量样本某个特征列取值范围的平均值。
- 方差:衡量样本某个特征列取值范围的离散程度。
- 协方差矩阵和相关系数:衡量样本特征列之间线性相关性。
4.1. 相关系数(Correlation Coefficient)
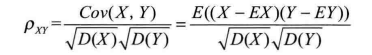
相关系数是衡量两个特征列之间相关程度的一种方法,其取值范围是[-1,1]。相关系数的绝对值越大,表明特征列X与Y的相关度越高。当X与Y线性相关时,相关系数取值为1(正线性相关)或-1(负线性相关)。
# 手动计算
vec1 = np.array([1, 1, 0, 1, 0, 1, 0, 0, 1])
vec2 = np.array([0, 1, 1, 0, 0, 0, 1, 1, 1])
Ev1 = vec1.mean() # np.mean(vec1)
Ev2 = vec2.mean()
Dv1 = vec1.std() # np.std(vec1)
Dv2 = vec2.std()
corref = np.mean(np.multiply(vec1-Ev1, vec2-Ev2))/(Dv1*Dv2) # output: 0.349999
# Numpy库函数
matV = np.mat([vec1, vec2])
np.corrcoef(matV)
'''
输出:
array([[ 1. , -0.35],
[-0.35, 1. ]])
'''

4.2. 相关距离(Correlation Distance)
相关系数矩阵的含义是:如果把第一个特征列作为参照数据(自己与自己的相关程度为1),那么第二个与第一个的相关程度是98%。
4.3. 马氏距离(Mahalanobis Distance)
马氏距离的定义:有M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到μ的距离为:
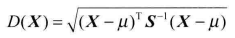
而其中xi与Xj之间的马氏距离为:
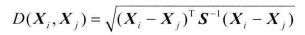
若协方差矩阵是单位矩阵(各个样本向量之间独立同分布),则公式变成欧式距离公式:

若协方差是对角矩阵,则公式变成可标准化的欧式距离公式。
from numpy import *
matV = mat([[1,1,0,1,0,1,0,0,1], [0,1,1,0,0,0,1,1,1]])
covinv = linalg.inv(cov(matV))
tp = matV.T[0] - matV.T[1]
distma = sqrt(dot(dot(tp,covinv), tp.T))
# output: matrix([[2.02547873]])
马氏距离的优点:量纲无关,排除变量之间的相关性的干扰。
5. 空间变换
5.1. 向量的空间变换
所谓向量与矩阵的乘法就是一个向量从一个线性空间(坐标系),通过选取一个新的基底([a1,a2]构成的新坐标系),变换到这个新基底构成的另一个线性空间的过程。
需要特别说明的是,一个向量的线性变换在几何上表现为缩放和旋转两个动作,以及这两个动作的组合—拉伸、压缩等。注意,这些动作的一个共性是都要通过原点。
6. 向量组的空间变换——理解矩阵乘法
左边的矩阵被定义为一个向量组,其列数被认为向量的维度;右边的矩阵被定义为个线性空间,相乘运算就是将这个向量组线性变换到新的线性空间中。也就是说,右边矩阵的行数最少要满足是由基底向量构成的线性空间的维度,或方程组的秩。这样就保证了这个变换必然存在。
6.1. 线性变换——特征值与特征向量
矩阵乘法对应了一个变换,是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中,原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换,不对这些向量产生旋转的效果,那么这些向量就称为这个矩阵的特征向量,伸缩的比例就是特征值。
7. 数据的归一化
归一化方法有两种形式:一种是把数值变为 (0, 1) 之间的小数;一种是把有量纲表达式变为无量纲表达式。
数据标准化:归一化在 (0,1) 之间是统计的概率分布,在 (-1, +1) 之间是统计的坐标分布。
量纲变换:不同量纲之间的数值是不具有可比性的,然而通过无量纲化,有纲量变成了无钢量。
7.1. 对欧式距离的标准化

from numpy import *
M = mat([[1,2,3], [4,9,16]])
Vdiff = M[0] - M[1]
print( sqrt(Vdiff * Vdiff.T) )
# Norm
Dmat = std(M.T, axis=0)
normVmat = (M - mean(M)) / Dmat.T
normv12 = normVmat[0] - normVmat[1]
print( sqrt( normv12 * normv12.T) )



