【入门】机器学习基础理论
1. 线性回归
回归分析最典型的例子就是“房价预测”。

1.1. 代价函数

1.1.1. 相关系数
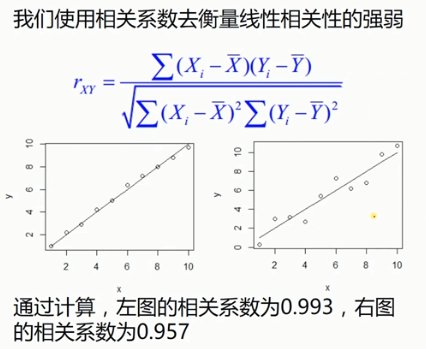
1.1.2. 决定系数

y为真实值,加 - 表示均值,加 ^ 表示预测值。
1.2. 梯度下降法

1.2.1. 用梯度下降法求解线性回归

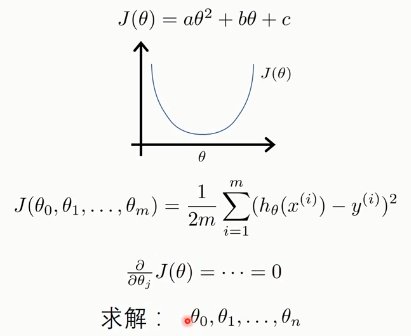
对代价函数J(θ)的求偏导,并利用梯度下降法更新权值,不断迭代……
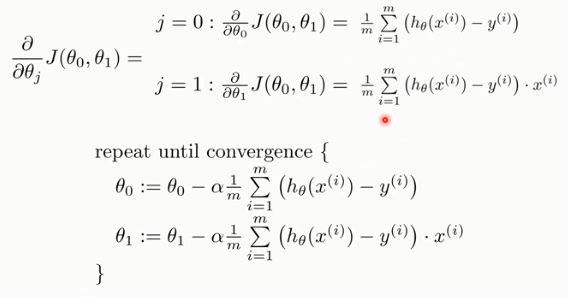
1.3. 多元线性回归
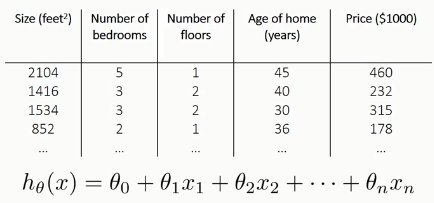
模型方程,以及代价函数:

运用梯度下降法(求偏导,迭代更新权值):

1.4. 多项式回归
1.5. 标准方程法
例如:以下为多元房价特征,进行房价预测:
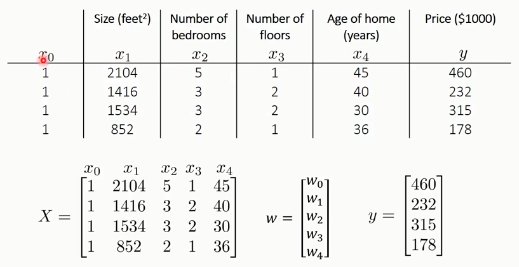
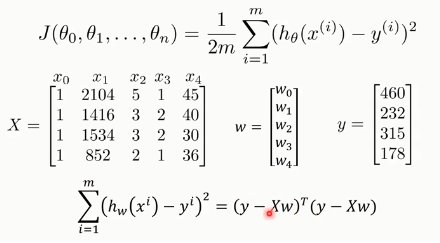
这里,将多个特征作为方程的因变量(多元特征向量),对w求导时就涉及到向量的导数:



1.5.1. 对比梯度下降法与标准方程法

2. 其他概念
2.1. 数据归一化

2.1.1. 均值标准化

2.2. 交叉验证法
适用于数据较少时对特征的训练
2.3. 过拟合
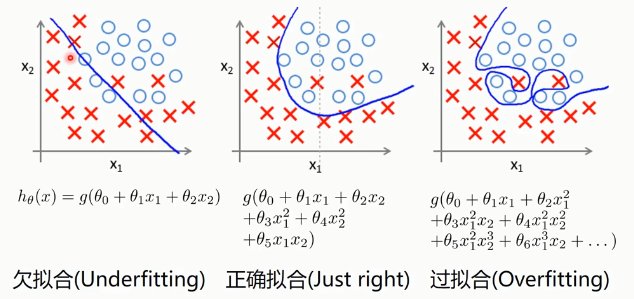
2.4. 正则化(Regularized)
用于防止过拟合

3. 岭回归(Ridge Regression)

代价函数,采用L2正则化:
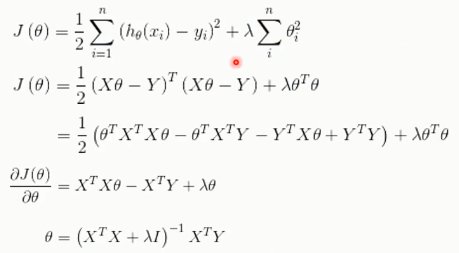

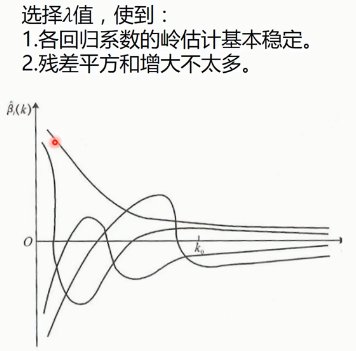
3.1. LESSO


4. 逻辑回归
Sigmoid/Logistic Function
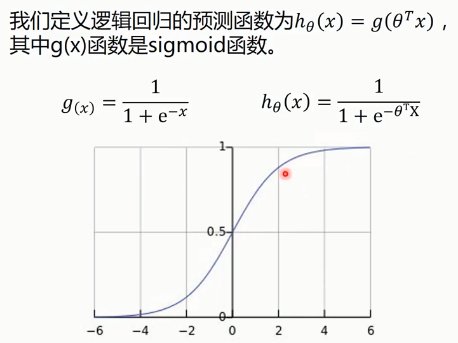
决策边界
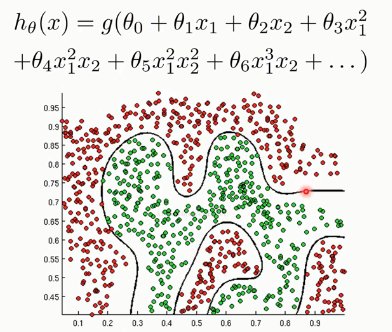
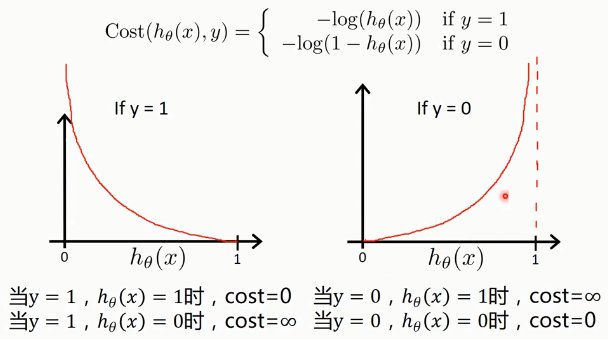
逻辑回归的代价函数
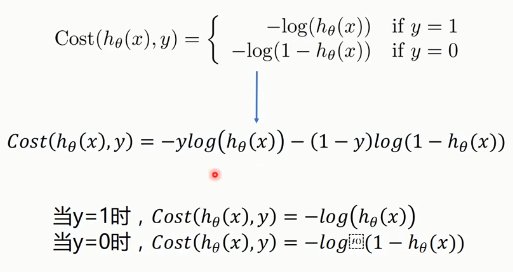
利用梯度下降法求解代价函数的最小值:

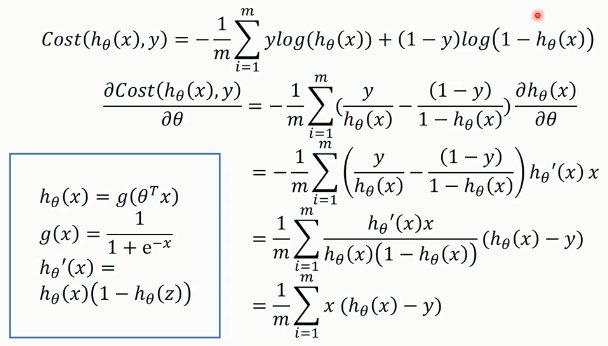
多分类问题
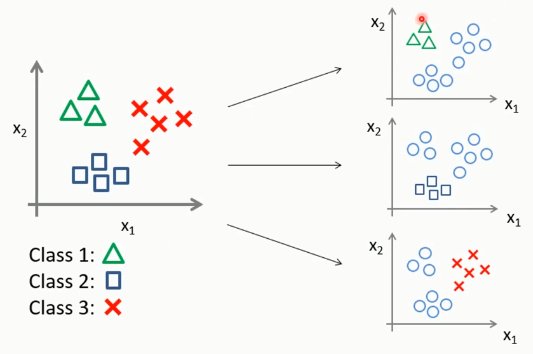
逻辑回归的正则化

4.1. 正确率和召回率


正确率与召回率的指标

5. KNN
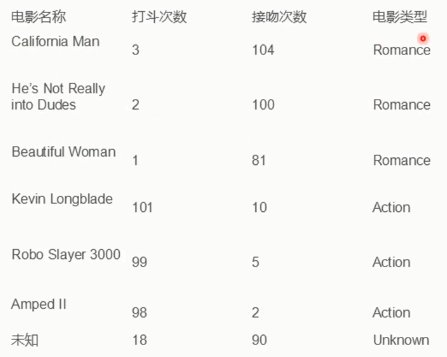
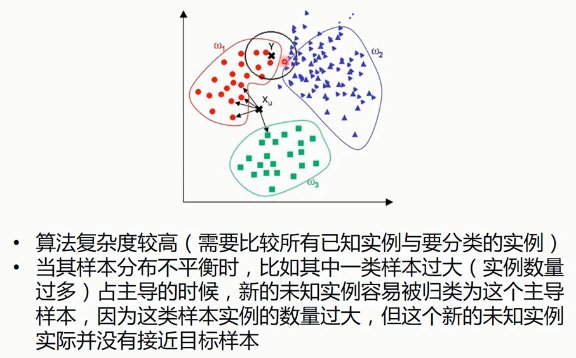
6. 决策树
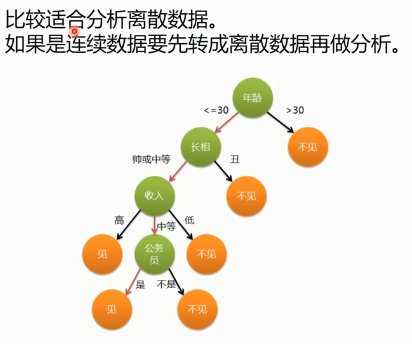
6.1. 熵


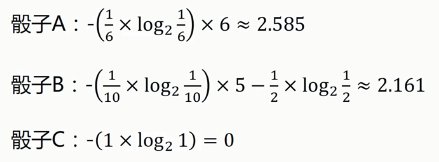
6.2. ID3算法


6.3. C4.5算法

6.4. CART算法




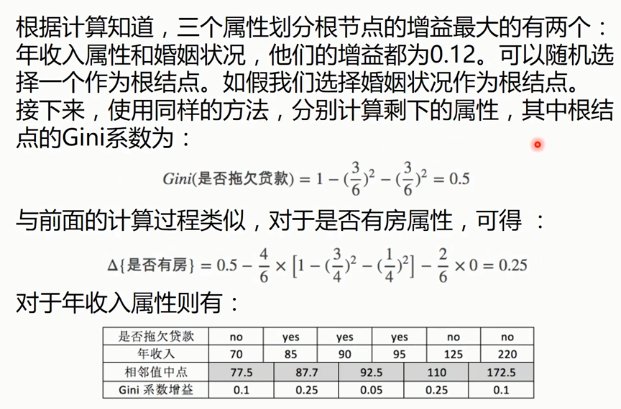
6.5. 剪枝:预剪枝、后剪枝
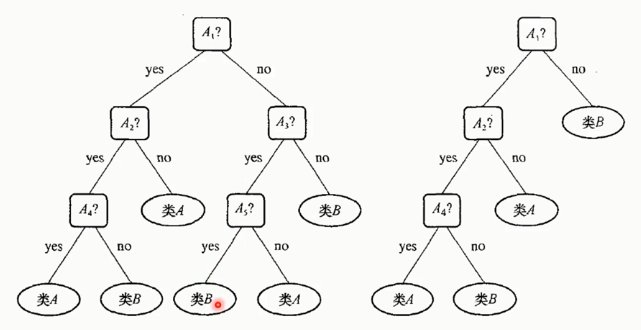
6.6. 决策树的评价(适用领域)
有点:小规模数据集有效
缺点:
- 处理连续变量不好
- 类别较多时,错误增加的比较快
- 不能处理大量数据
7. 集成学习

7.1. Bagging
首先,进行一种有放回的抽样~
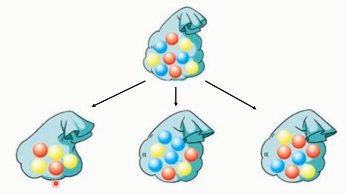

每个数据集,都采用一种不同的学习算法(或者同一个算法,得到不同的模型)
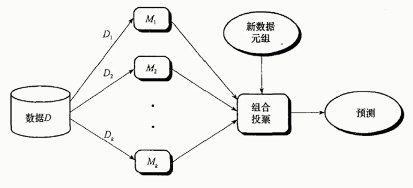
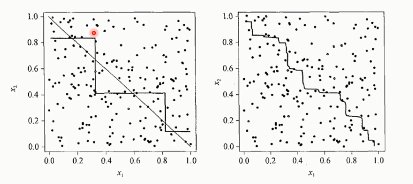
效果如下:
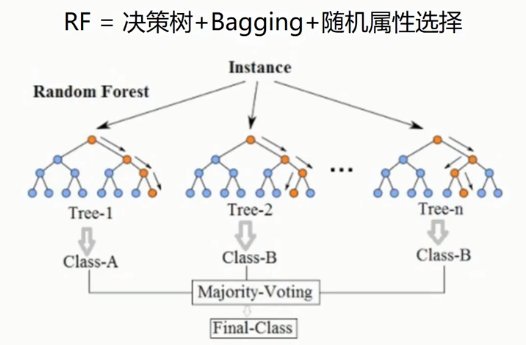
7.2. 随机森林

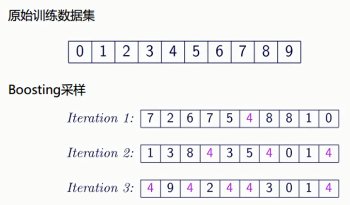
7.3. boosting(Adaptive Boosting,自适应增强)
学习器的重点放在“容易”出错的地方——增加出错数据的概率(样本采样的权值)。

7.4. Stacking
使用多个不同的分类器对训练集进行预测,把预测得到的结果作为次级分类器的输入。次级分类器的输出则是整个模型的最终预测结果。
7.5. 集成学习的总结
——人多力量大、集众家之言,以民主的方式决定正确的预测结果。

8. 贝叶斯分析




8.1. 朴素贝叶斯
多特征时的概率计算,会导致计算量巨大……
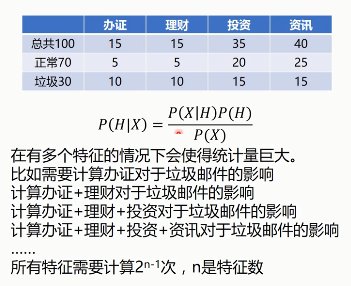
朴素贝叶斯算法,会假设特征X1, X2, X3...之间是相互独立的,则
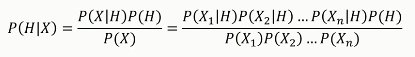
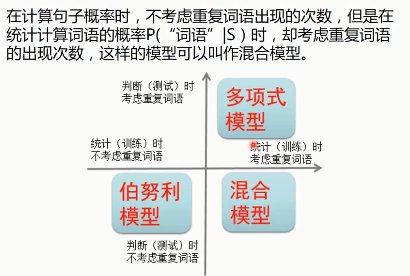
8.1.1. 贝叶斯多项式模型

8.1.2. 伯努利模型
8.1.3. 混合模型
8.1.4. 高斯模型
常用于处理连续性变量。

8.1.5. 大脑中的贝叶斯

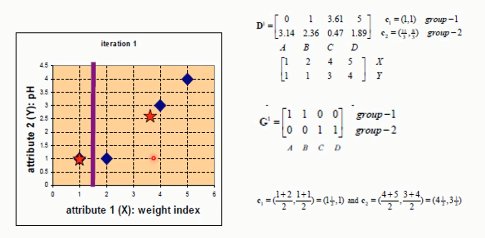
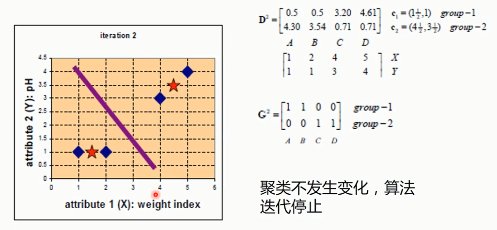
9. 聚类算法
无监督式学习——

9.1. K-MEANS
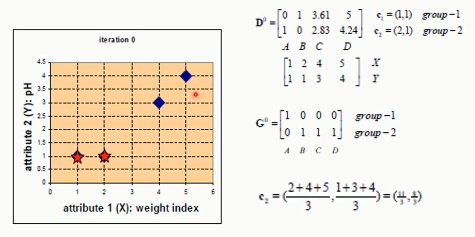
G:归类
C:计算重心,然后调整中心点