激活函数,损失函数,优化器
1. 激活函数
1.1. 为什么需要激活函数(激励函数)
在神经网络中,对于图像,我们主要采用了卷积的方式来处理,也就是对每个像素点赋予一个权值,这个操作显然就是线性的。但是对于我们的样本来说,不一定是线性可分的,为了解决这个问题,我们可以进行线性变化,或者我们引入非线性因素,解决线性模型所不能解决的问题。
这就是为什么要有激活函数:激活函数是用来加入非线性因素的,因为线性模型的表达力不够。
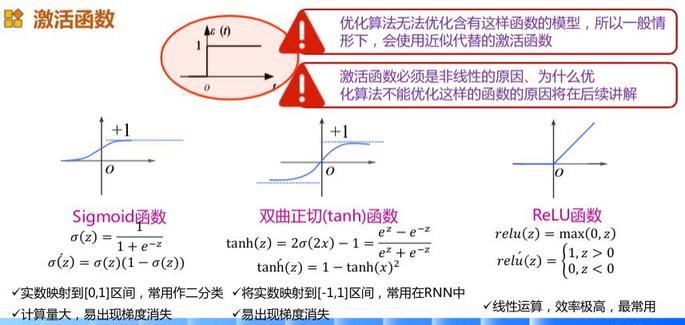
所以激活函数,并不是去激活什么,而是指如何把“激活的神经元的特征”通过函数把特征保留并映射出来(保留特征,去除一些数据中是的冗余),这是神经网络能解决非线性问题关键。
1.1.1. ReLU
简称为“抹零” 😃
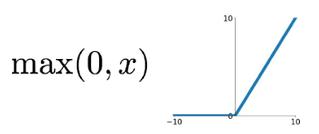

优点:
- 相较于sigmoid和tanh函数,relu对于SGD(梯度下降优化算法) 的收敛有巨大的加速作用(Alex Krizhevsky指出有6倍之多)。有人认为这是由它的线性、非饱和的公式导致的。
- 相比于sigmoid和tanh,relu只需要一个阈值就可以得到激活值,而不用去算一大堆复杂的(指数)运算。
- relu在x<0时是硬饱和。当x>0时一阶导数为1,所以relu函数在x>0时可以保持梯度不衰减,从而有效缓解了梯度消失的问题。
- 在没有无监督预训练的时候也能有较好的表现。
- 提供了神经网络的稀疏表达能力。
缺点:随着训练的进行,部分输入会落到硬饱和区,导致对应的权重无法更新。我们称之为“神经元死亡”。
实际中,如果学习率设置得太高,可能会发现网络中 40% 的神经元都会死掉(在整个训练集中这些神经元都不会被激活)。合理设置学习率,会降低这种情况的发生概率。
除了relu本身外,TensorFlow后续又有相关ReLU衍生的激活函数,比如:ReLU6、SReLU、Leaky ReLU 、PReLU、RReLU、CReLU。
LReLU、PReLU与RReLU是relu激活函数的改进版本,图像如下:
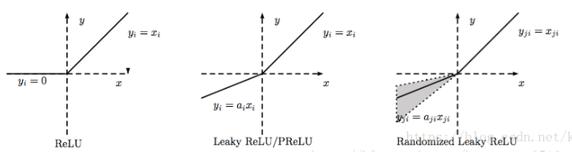
1.1.2. sigmod
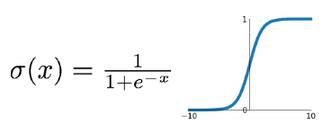
优点:它输出映射在(0,1)内,单调连续,非常适合用作输出层;并且求导比较容易。
缺点:具有软饱和性,一旦输入落入饱和区,一阶导数就变得接近于0,很容易产生梯度消失;指数运算相对耗时;sigmoid 函数关于原点中心不对称;并且对于权重矩阵的初始化必须特别留意。比如,如果初始化权重过大,那么大多数神经元将会饱和,导致网络就几乎不学习。
饱和性:当|x|>c时,其中c为某常数,此时一阶导数等于0,通俗的说一阶导数就是上图中的斜率,函数越来越水平。
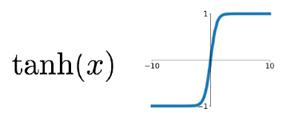
1.1.3. tanh
tach也是传统神经网络中最常用的激活函数,与sigmoid一样也存在饱和问题,但它的输出是0中心的,因此实际应用中tanh比sigmoid 更受欢迎。tanh函数实际上是一个放大的sigmoid函数。
1.2. Pytorch常见激活函数
作用:把卷积层输出结果做非线性映射。
常用到的激活函数包括:
- sigmoid:
torch.nn.functional.sigmoid(input)(已经不推荐使用了) - tanh:
torch.nn.functional.tanh(input) - Relu:
torch.nn.functional.relu(input, inplace = False) - Leaky Relu:
torch.nn.functional.leaky_relu(input, negative_slope=0.01, inplace=False) - EReLU
- Maxout
2. 损失函数
2.1. Keras内置的损失函数
2.1.1. Keras core Loss
model.compile(loss='目标函数 ', optimizer='adam', metrics=['accuracy'])
损失函数,或称目标函数,是网络中的性能函数,也是编译一个模型必须的两个参数之一。由于损失函数种类众多,下面以keras官网手册的为例。
在官方keras.io里面,有如下资料:
-
mean_squared_error或mse
-
mean_absolute_error或mae
-
mean_absolute_percentage_error或mape
-
mean_squared_logarithmic_error或msle
-
squared_hinge
-
hinge
-
binary_crossentropy(亦称作对数损失,logloss)
-
categorical_crossentropy(亦称作多类的对数损失)
注意使用该目标函数时,需要将标签转化为形如(nb_samples, nb_classes)的二值序列
-
sparse_categorical_crossentrop:
如上,但接受稀疏标签。注意,使用该函数时仍然需要你的标签与输出值的维度相同,你可能需要在标签数据上增加一个维度:np.expand_dims(y,-1)
-
kullback_leibler_divergence
从预测值概率分布Q到真值概率分布P的信息增益,用以度量两个分布的差异.
-
cosine_proximity
即预测值与真实标签的余弦距离平均值的相反数
2.1.2. mean_squared_error
顾名思义,意为均方误差,也称标准差,缩写为MSE,可以反映一个数据集的离散程度。
标准误差定义为各测量值误差的平方和的平均值的平方根,故又称为均方误差。
公式:
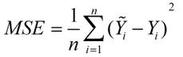
可以理解为一个从n维空间的一个点到一条直线的距离的函数。(此为在图形上的理解,关键看个人怎么理解了)
2.1.3. mean_absolute_error
译为平均绝对误差,缩写MAE。
平均绝对误差是所有单个观测值与算术平均值的偏差的绝对值的平均。
公式:
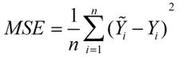
2.1.4. binary_crossentropy
即对数损失函数,log loss,与sigmoid相对应的损失函数。
公式:L(Y,P(Y|X)) = -logP(Y|X)
该函数主要用来做极大似然估计的,这样做会方便计算。因为极大似然估计用来求导会非常的麻烦,一般是求对数然后求导再求极值点。
损失函数一般是每条数据的损失之和,恰好取了对数,就可以把每个损失相加起来。负号的意思是极大似然估计对应最小损失。
2.1.5. categorical_crossentropy
多分类的对数损失函数,与softmax分类器相对应的损失函数,理同上。
tip:此损失函数与上一类同属对数损失函数,sigmoid和softmax的区别主要是,sigmoid用于二分类,softmax用于多分类。
注意: 当使用 categorical_crossentropy 损失时,你的目标值应该是分类格式 (即,如果你有 10 个类,每个样本的目标值应该是一个 10 维的向量,这个向量除了表示类别的那个索引为 1,其他均为 0)。 为了将 整数目标值 转换为 分类目标值,你可以使用 Keras 实用函数 to_categorical:
from keras.utils.np_utils import to_categorical
categorical_labels = to_categorical(int_labels, num_classes=None)
2.2. Pytorch内置的损失函数
2.2.1. 交叉熵:用于分类
-
熵(Entropy)
-
交叉熵(Cross Entropy)
- OneHot编码
- 二分类: Binary Classification
-
Softmax函数
在Pytorch里,nn.Cross_Entropy()损失函数已经将
softmax() -> log2() -> nll_loss()绑在一起。因此,使用了Cross_Entropy()函数,函数里的paramets必须是logits。全连接层后面不需要再添加softmax层,此处也是与TensorFlow不同之处。
2.2.2. 均方误差(MSE): 用于回归
回归问题解决的是对具体的数值进行预测。例如,房价预测、销量预测都是回归问题。这些问题需要预测的不是一个事先定义好的类别,而是一个任意实数,解决回归问题的神经网络一般只有一个输出节点,这个节点的输出值就是预测值。对于回归问题常用的损失函数为均方误差(MSE,mean squared error): nn.MSELoss() 。
3. 反向传播
反向传播算法就是一个有效的求解梯度的算法,本质上其实就是一个链式求导法则的应用。
3.1. 链式法则
链式法则是微积分中的求导法则,用于求一个复合函数的导数,是在微积分的求导运算中一种常用的方法。
例如:f(x,y,z) = (x+y)*z
本来可以直接求出函数的关于x、y、z的导数,但是此次采用链式求导法则:
令 q = x+y
则 f = qz
对于这两个式子分别求出它们的微分 ∂f / ∂q = z, ∂f / ∂z = q ,其中,∂q / ∂y = 1, ∂q / ∂x = 1 。
因需要求出 ∂f / ∂y , ∂f / ∂x , ∂f / ∂z ,那么f(x,y,z)的连续求导为:
∂f / ∂x = (∂f / ∂q) * ( ∂q / ∂x) = z
∂f / ∂y = (∂f / ∂q) * ( ∂q / ∂y) = z
∂f / ∂z = q = x + y
以上便是链式求导法则的核心,通过连续求导,便得出了 ∂f / ∂y , ∂f / ∂x , ∂f / ∂z 。
3.2. 神经网络优化算法
Pytorch 提供了 torch.optim 模块。参数的梯度可以通过求偏导的方式计算,对于参数Θ,其梯度为 ∂J(Θ)/∂Θ ,有了梯度,还需要定义一个学习率来定义每次参数更新的幅度,则得到参数更新的公式为:
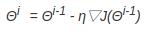
3.2.1. SGD
随机梯度下降法(Stochastic Gradient Descent):每次使用一批(batch)数据进行梯度的计算。而不是计算全部数据的梯度,因为现在的深度学习的数据量都特别大,所以每次都计算所有数据的梯度是不现实的,这样会导致运算的时间特别的长,并且每次都计算全部的梯度还失去了一些随机性,容易陷入局部误差,所以,SGD能减小收敛所需要的迭代次数,使用随机梯度下降法可能每次都不是朝着真正最小的方向,但是这样反而容易跳出局部极小点。

3.2.2. Momentum
Momentum就是在随机梯度下降的同时,增加动量,可以把它理解为增加惯性,可解释为利用惯性跳出局部极小值点。

3.2.3. Adagrad
Adagrad优化器,是基于SGD的一种算法,它的核心思想是对比较常见的数据给与它比较小的学习率去调整参数,对于比较罕见的数据给予它比较大的学习率去调整参数,适合用于数据稀疏的数据集。Adagrad主要的优势在于不需要人为的调节学习率,它可以自动调节。它的缺点在于,随着迭代次数的增多,学习率也会越来越低,最终会趋向于0.
3.2.4. RMSprop
RMSprop不会再将前面有所的梯度求和,而是通过一个衰减率将其变小,使用了一种平滑平均的方式,越靠前面的梯度对自适应的学习率影响越小,这样就能更加有效地避免Adagrad学习率一直递减太多的问题,能够更快的收敛。
3.2.5. Adam
Adam是一阶基于梯度下降的算法,基于自适应低阶矩估计优化器,效果比RMSprop好。其还有一种Adamax优化算法是基于无穷大范数的Adam算法的一个变种。
Adam像Adadelta和RMSprop一样会存储之前衰减的平方梯度,同时它也会保存之前衰减的梯度。经过一些处理之后再使用类似Adadelta和RMSprop的方式更新参数。
4. Dropout函数
Dropout函数是Hintion在2012年提出的,为了防止模型过拟合,在每个训练批次中,通过忽略一般的神经元即让一部分的隐层节点值为0,可明显地减少过拟合现象。
torch.nn.functional.dropout(input, p = 0.5,training = False,inplace = False)
torch.nn.functional.alpha_dropout(input, p = 0.5,training = False)
torch.nn.functional.dropout2d(input, p = 0.5,training = False,inplace = False)
torch.nn.functional.dropout3d(input, p = 0.5,training = False,inplace = False)
注:pytorch中的 p = 0.5 ,表示的是dropout_prob;而TensorFlow中的 p = 0.5 ,表示keep_prob。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号