【转载】光照不均匀图像分割技巧
1. 案例描述
在数字图像处理中，图像分割是很关键的一步，当图像质量较好，光照很均匀的时候只需用全局阈值的方法就能很完美地完成图像分割任务，但是有些时候会遇到光照不均匀的现象，这个时候就需要用一些技巧才能达到比较好的分割效果。
我们先看一个实例，下面图1和图3为做硬币面额识别拍摄的，可以看到，由于硬币表面的反光以及打光角度的原因，图片存在严重的光照不均现象。
如果对两幅图像直接进行全局阈值可以得到图2和图4的结果，可以看到分割的效果很差，比如第一幅，右上角的光照要强一些，而且右上角的硬币存在一定的反光，灰度值整体偏高，导致最后分割效果很差。第二幅则是左边部分光照太强，左边的硬币分割效果很差。
2. 方式1: 分块阈值
通过将图像分割成若干块，分别进行阈值分割，可以在一定程度上解决光照或反射造成的不均匀影响。选择的块要足够小，以便每个块的光照都近似均匀的，这样自动阈值时，在高灰度区域就会用高阈值分割，在低灰度区域就会用低阈值分割。
图5为分块结果，示例中分块与硬币大小相当，分完块之后就可以按块进行全局阈值法（这里采用常用的最大类间方差法，otsu法）处理了，但是需要注意的是有的块中只有背景，这个时候需要进行判断，排除对这种块的处理。
笔者在计算出各个块的可分性度量之后，发现区分效果并不是很好，后来通过分析最大类间方差法，有个想法就是用分割阈值处的类间平均灰度差判断图像块的可分性，当图像中只有背景或只有物体时，由于灰度值比较接近，则用otsu法算出的“背景”和“前景”平均灰度差（类间灰度差）会很小。
如图5中各块标注的文字所示，T为分割阈值，d为类间平均灰度差，可以看到当块中只有背景时，平均灰度差与有物体时相差很大，选取特征区分效果很好。本示例中，选灰度差20就能将两种不同的块很好的区分开。
之后仅对既有物体又有背景的块进行自动阈值处理、二值化、填充孔洞，可以得到图6的结果，可以看到每个硬币都被很好的分割出来：
3. 方式2: 顶帽变换和底帽变换
这两个变换的主要应用之一是，用一个结构元通过开操作或闭操作从一副图像中删除物体，而不是拟合被删除的物体。然后，差操作得到一副仅保留已删除分量的图像。顶帽变换用于暗背景上的亮物体，而底帽变换则用于相反的情况。由于这一原因，当谈到这两个变换时，常常分别称为白顶帽变换和黑底帽变换。它们一个重要用途是校正不均匀光照的影响。
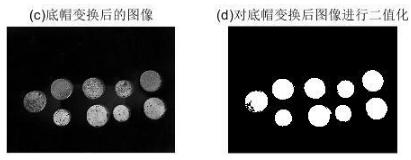
由于原图是背景亮，前景暗，对原图进行底帽变换以解决光照不均匀的问题，这里先给出处理结果，如下图，可以看到底帽变换后的图像删除了大部分非均匀背景，最后阈值处理后，左边的硬币被分割出来，有少量残缺，但是影响不大，后续可以通过形态学的其他处理将残缺补齐。
那么为什么底帽变换或顶帽变换可以达到上述效果呢，下面以底帽变换为例，通过图像的灰度三维图来进行解释。
底帽变换为f的闭操作减去f，闭运算可以几何意义是让球体紧贴在曲面的上表面滚动，此时球体任何部分所能达到的最低点即构成了闭运算f∙b的曲面。
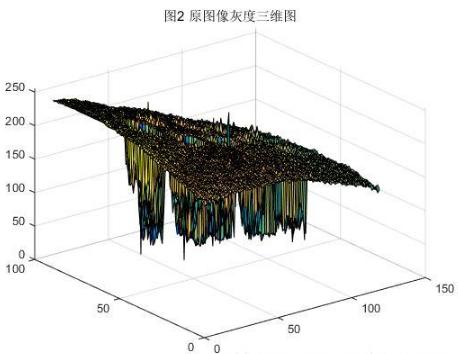
图2为原图灰度三维图，上方弯曲的走势显示了图像各部分光照不均匀造成的背景灰度不均现象，其中凹陷对应图像中灰度值比较小的区域，也就是图像中的硬币。
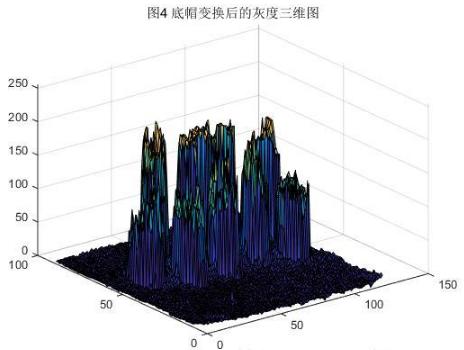
通过选取大于硬币大小的合适结构元，可以看成一个球体在灰度曲面上滚动，球体下表面的轨迹构成闭运算的曲面，如图3所示，原图中的凹陷都被填上，可以近似代表不均匀的背景。闭运算完之后再减去原图像即可得到背景近似均匀的图像，如图4所示，对应的灰度图可以看图1（c）,可以看到不均匀的背景被大致去除，这将十分有助于后面的阈值分割。
