程序员的数学2-概率统计
《程序员的数学2:概率统计》
1. 导论
1.1. 经典的“三扇门”问题
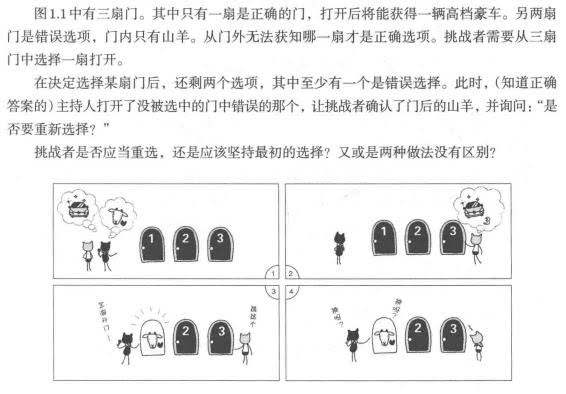

概率是一种很抽象的概念,如果我们仅凭直觉判断,很难清晰理解他的本质。
开启“上帝视角”
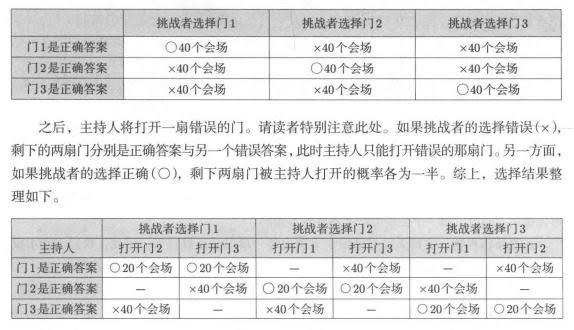
看到了吗?重点来了——“如果挑战者选择错误,剩下的两扇门分别是正确或错误答案,此时主持人只能打开错误的那扇门”。

1.2. 概率空间
概率空间的三要素(Ω,F,P)
- Ω: 包含概率空间最小不可分的独立事件
- F: 定义事件可能的相互组合
- P: 给定F中组合发生的可能性大小
1.3. 数学期望
数学期望是对随机变量中心位置的一种度量。是试验中每次可能结果的乘以其结果的总和。简单说,它是概率中的平均值,可以用期望对比两套方案。
1.4. 方差 & 标准差
方差是对风险的度量,即随机变量的变异性。
numpy的API:
- np.var(): 均方差
- np.std(): 标准差
- np.var(): 标准差的平方(方差)
a = np.random.randint(0, 10, (2, 3))
1.4.1. 有了方差为什么需要标准差?
标准差和均值的量纲(单位)是一致的,在描述一个波动范围时标准差比方差更方便。
比如一个班男生的平均身高是 170cm, 标准差是 10cm, 那么方差就是 100cm^2。可以进行的比较简便的描述是本班男生身高分布是 170±10cm ,方差就无法做到这点。
再举个例子,从正态分布中抽出的一个样本落在 [μ-3σ, μ+3σ] 这个范围内的概率是99.7%,也可以称为“正负3个标准差”。如果没有标准差这个概念,我们使用方差来描述这个范围就略微绕了一点。
1.5. 大数定理
随着样本的增加,样本的平均数将接近于总体的平均数,故推断中,一般会使用样本平均数估计总体平均数。
大数定律讲的是样本均值收敛到总体均值。
1.6. 中心极限定理
独立同分布的事件,具有相同的期望和方差,则事件服从中心极限定理。他表示了对于抽取样本,n足够大的时候,样本分布符合 x~N(μ,σ^2) 。
中心极限定理告诉我们,当样本量足够大时,样本均值的分布慢慢变成正态分布。
2. 离散概率分布
离散概率分布计算公式用概率质量函数PMF(Probability Mass Function):之所以叫做质量,是因为离散是点,默认体积为1。
2.1. 两点分布(伯努利分布)
伯努利试验是在同样的条件下重复地、各次之间相互独立地进行的一种试验,最常见的例子为抛硬币。
即只进行一次伯努利试验,该事件发生的概率为p,不发生的概率为1-p。这是一个最简单的分布,任何一个只有两种结果的随机现象都服从0-1分布。
- 期望:
E = p - 方差:
D = p*(1-p)^2+(1-p)*(0-p)^2 = p*(1-p)
2.2. 二项分布(n重伯努利分布)
即做n个两点分布的实验。应用场景:对于已知次数n,关心发生k次成功。
E = n*p(预期成功次数)D = np(1-p)
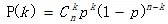
from scipy.stats import binom
fig,ax = plt.subplots(1,1)
n = 100
p = 0.5
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = binom.stats(n,p,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时,ppf就是p(X<x)=0.01时的x值。
x = np.arange(binom.ppf(0.01, n, p),binom.ppf(0.99, n, p))
ax.plot(x, binom.pmf(x, n, p),'o')
plt.title(u'二项分布概率质量函数')
plt.show()
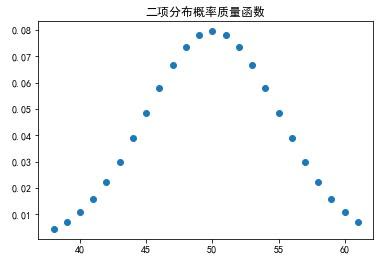
观察概率分布图,可以看到,对于n = 100次实验中,有50次成功的概率(正面向上)的概率最大。
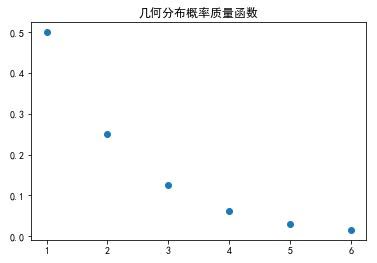
2.3. 几何分布
应用场景: 想要知道尝试某件事情多次能取得第一次成功的概率。
E = 1/p(预期E次后取得第1次成功)D = (1-p)/p^2
from scipy.stats import geom
fig,ax = plt.subplots(1,1)
p = 0.5
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = geom.stats(p,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时,ppf就是p(X<x)=0.01时的x值。
x = np.arange(geom.ppf(0.01, p),geom.ppf(0.99, p))
ax.plot(x, geom.pmf(x, p),'o')
plt.title(u'几何分布概率质量函数')
plt.show()
2.4. 泊松分布
某个范围内,发生某件事情k次的概率有多大。(如一天内中奖的次数,一个月内机器发生故障的次数,一段道路发生交通事故的次数)
定义 λ :单位时间/面积下,随机事件的平均发生率。
- E = λ
- D = λ
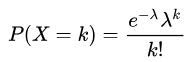
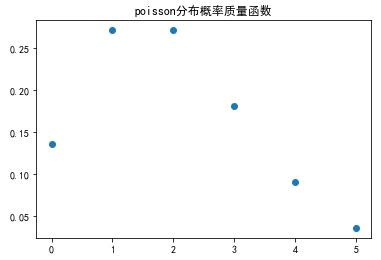
假设某地区,一年中发生枪击案的平均次数为2。
from scipy.stats import poisson
fig,ax = plt.subplots(1,1)
mu = 2
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = poisson.stats(mu,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时,ppf就是p(X<x)=0.01时的x值。
x = np.arange(poisson.ppf(0.01, mu),poisson.ppf(0.99, mu))
ax.plot(x, poisson.pmf(x, mu),'o')
plt.title(u'poisson分布概率质量函数')
plt.show()
因此,一年内的枪击案发生次数的分布如下图所示:
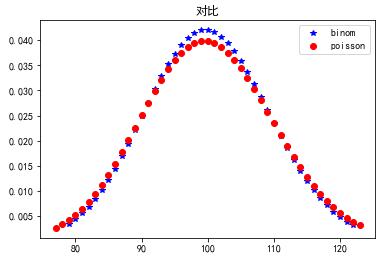
泊松分布的形状会随着平均值的不同而有所变化。下图显示了泊松分布与二项分布的对比:
3. 连续概率分布
连续概率分布计算公式用概率密度函数PDF(Probability Density Function):之所以叫密度,是因为连续随机变量概率计算的是面积。
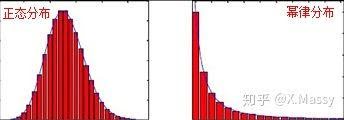
3.1. 正态分布
世界上绝大部分的分布都属于正态分布,下面列出的变量的分布都比较接近正态分布:
- 人群的身高
- 成年人的血压
- 传播中的粒子的位置
- 测量误差
- 回归中的残差
- 人群的鞋码
- 一天中雇员回家的总耗时
- 教育指标
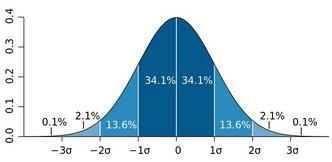
正态随机变量有69.3%的值在均值加减一个标准差的范围内,95.4%的值在两个标准差内,99.7%的值在三个标准差内。这条经验法则可以帮助我们快速计算数据的大体分布。
E = μD = σ^2
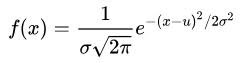
u代表均值,σ代表标准差,两者不同的取值将会造成不同形状的正态分布。均值表示正态分布的左右偏移,标准差决定曲线的宽度和平坦,标准差越大曲线越平坦。
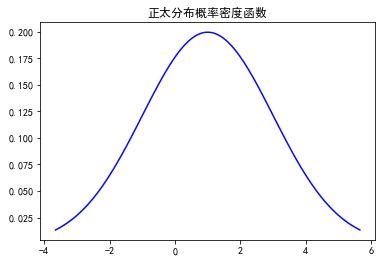
from scipy.stats import norm
fig,ax = plt.subplots(1,1)
loc = 1
scale = 2.0
#平均值, 方差, 偏度, 峰度
mean,var,skew,kurt = norm.stats(loc,scale,moments='mvsk')
print mean,var,skew,kurt
#ppf:累积分布函数的反函数。q=0.01时,ppf就是p(X<x)=0.01时的x值。
x = np.linspace(norm.ppf(0.01,loc,scale),norm.ppf(0.99,loc,scale),100)
ax.plot(x, norm.pdf(x,loc,scale),'b-',label = 'norm')
plt.title(u'正太分布概率密度函数')
plt.show()
3.1.1. 标准正态分布
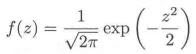
特征: 方差恰好为1。
4. 联合分布, 边缘分布

联合概率与边缘概率的关系如下:
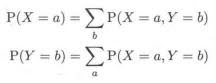
实例:

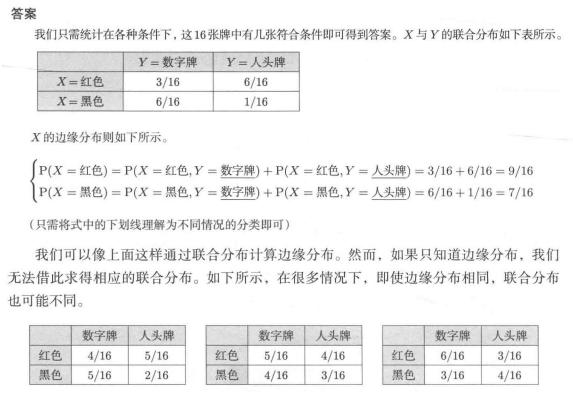
5. 条件分布
条件概率是指事件A在另外一个事件B已经发生条件下的发生概率。条件概率表示为: P(A|B) ,读作“在B条件下A的概率”。条件概率可以用决策树进行计算。
条件概率的谬论是假设 P(A|B) 大致等于 P(B|A) 。

5.1. 条件概率的计算公式
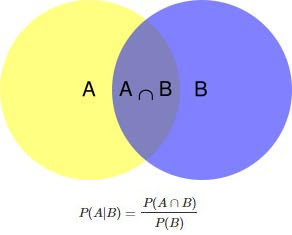
或者写为:
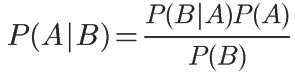
注:条件概率中的竖线符号 | ,在英文中读作 given 。
5.2. 全概率公式
假定样本空间S,是两个事件A与A'的和。
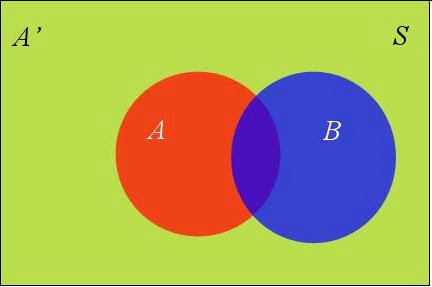
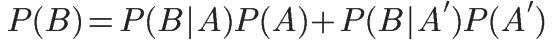
它的含义是,如果A和A'构成样本空间的一个划分,那么事件B的概率,就等于A和A'的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
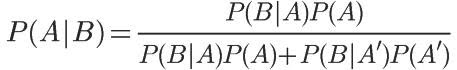
推广:
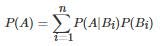
这个推论的要点是不同的B事件互斥(不相交),且它们的并集是 Ω 。每个元素都必须且只能进入一个 Bi 。在这样的条件下,我们说[B1,B2,...,Bn]是样本空间的一个 分割(partion) 。 这就像二战后的德国被分区占领一样,每个 Bi 是一个占领区。
5.3. 贝叶斯推断
对条件概率公式进行变形,可以得到如下形式:
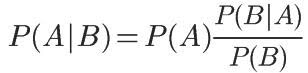
我们把P(A)称为"先验概率"(Prior probability),即在B事件发生之前,我们对A事件概率的一个判断。P(A|B) 称为"后验概率"(Posterior probability),即在B事件发生之后,我们对A事件概率的重新评估。P(B|A)/P(B) 称为"可能性函数"(Likelyhood),这是一个调整因子,使得预估概率更接近真实概率。
所以,条件概率可以理解成下面的式子:
后验概率 = 先验概率 x 调整因子
这就是贝叶斯推断的含义。我们先预估一个"先验概率",然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率",由此得到更接近事实的"后验概率"。
5.3.1. 实例1
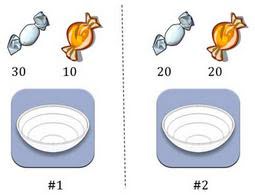
两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。现在随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
我们假定,H1表示一号碗,H2表示二号碗。由于这两个碗是一样的,所以 P(H1)=P(H2) ,也就是说,在取出水果糖之前,这两个碗被选中的概率相同。因此 P(H1)=0.5 ,我们把这个概率就叫做"先验概率",即没有做实验之前,来自一号碗的概率是0.5。
再假定,E表示水果糖,所以问题就变成了在已知E的情况下,来自一号碗的概率有多大,即求 P(H1|E) 。我们把这个概率叫做"后验概率",即在E事件发生之后,对 P(H1) 的修正。
根据条件概率公式,得到
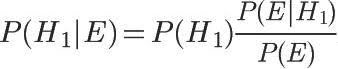
于是:
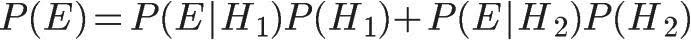
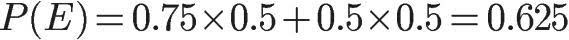
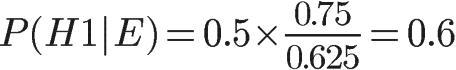
这表明,来自一号碗的概率是0.6。也就是说,取出水果糖之后,H1事件的可能性得到了增强。
5.3.2. 实例2

已知某种疾病的发病率是0.1%,即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病,它的准确率是0.99,即在患者确实得病的情况下,它有99%的可能呈现阳性。它的误报率是5%,即在患者没有得病的情况下,它有5%的可能呈现阳性。现有一个病人的检验结果为阳性,请问他确实得病的可能性有多大?
假定A事件表示得病,那么P(A)为0.001。这就是"先验概率",即没有做试验之前,我们预计的发病率。再假定B事件表示阳性,那么要计算的就是 P(A|B)。这就是"后验概率",即做了试验以后,对发病率的估计。
根据条件概率公式,
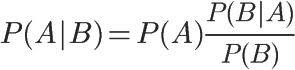
用全概率公式改写分母,
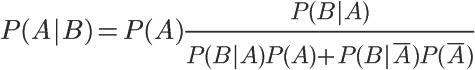
将数字代入,
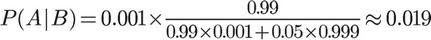
我们得到了一个惊人的结果,P(A|B)约等于0.019。也就是说,即使检验呈现阳性,病人得病的概率,也只是从0.1%增加到了2%左右。这就是所谓的"假阳性",即阳性结果完全不足以说明病人得病。
为什么会这样?为什么这种检验的准确率高达99%,但是可信度却不到2%?答案是与它的误报率太高有关。(【习题】如果误报率从5%降为1%,请问病人得病的概率会变成多少?)
有兴趣的朋友,还可以算一下"假阴性"问题,即检验结果为阴性,但是病人确实得病的概率有多大。然后问自己,"假阳性"和"假阴性",哪一个才是医学检验的主要风险?
5.4. 贝叶斯公式
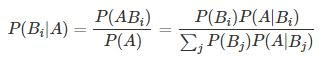
贝叶斯公式就是:已知事件A这个“结果”已经发生了,反过来研究造成事件A发生的原因--事件B1、事件B2...的概率是多少,这是一个“因果溯源”的过程。
6. 协方差矩阵
6.1. 协方差
标准差和方差一般是用来描述一维数据的,但现实生活我们常常遇到含有多维数据的数据集,最简单的大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集,我们当然可以按照每一维独立的计算其方差,但是通常我们还想了解更多,比如,一个男孩子的猥琐程度跟他受女孩子欢迎程度是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量。
协方差的计算公式
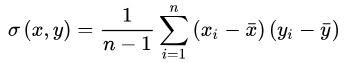
协方差的意义:如果结果为正值,则说明两者是正相关的(从协方差可以引出“相关系数”的定义)。
上一节提到的猥琐和受欢迎的问题是典型二维问题,而协方差也只能处理二维问题,那维数多了自然就需要计算多个协方差,比如n维的数据集就需要计算 n! / ((n-2)!*2) 个协方差,那自然而然的我们会想到使用矩阵来组织这些数据。
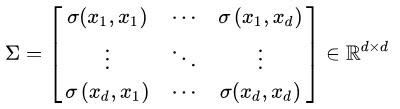
可见,协方差矩阵是一个对称矩阵,而且对角线是各个维度上的方差。
>>> x = [-2.1, -1, 4.3]
>>> y = [3, 1.1, 0.12]
>>> np.cov(np.vstack((x,y)))
[[ 11.71 -4.286 ]
[ -4.286 2.14413333]]
>>> np.cov(x, y)
[[ 11.71 -4.286 ]
[ -4.286 2.14413333]]
>>> np.cov(x)
11.71



 浙公网安备 33010602011771号
浙公网安备 33010602011771号