20135321余佳源——信息安全系统设计基础第三周学习总结
信息安全系统设计基础第三周学习总结
第四周:学习任务教材第二章
第四周(9.28-10.04):
学习计时:共10小时 读书:2 代码:2 作业:3 博客:3 |
学习目标 |
1. 理解二进制在计算机中的重要地位 2. 掌握布尔运算在C语言中的应用 3. 理解有符号整数、无符号整数、浮点数的表示 4. 理解补码的重要性 5. 能避免C语言中溢出,数据类型转换中的陷阱和可能会导致的漏洞 |
学习任务:
公式可以不看,习题不能不做,考核题目和课后习题类似,重点题目:
2.4、2.6、2.8、2.11、2.13、2.14、2.18、2.19、2.21、2.23、
2.24、2.25、2.27、2.29、2.33、2.34、2.39、2.40、2.42、2.43、
2.44、2.45、2.47、2.50、2.52、2.54
p20: 三种数字:无符号数、有符号数(2进制补码)、浮点数,信息安全系同学从逆向角度考虑为什么会产生漏洞
p22: 进制转换,注意拿二进制作中间结果就好转了
p25: gcc -m32 可以在64位机上(比如实验楼的环境)生成32位的代码
p26: 字节顺序是网络编程的基础,记住小端是"高对高、低对低",大端与之相反就可以了。
p28: 代码执行一下
p32: 能区分逻辑运算(结果是1或0)和位运算(结果是位向量),所有逻辑运算都可以用与、或、非表达(最大式、最小式),而与或非可以用"与非"或"或非"表达,所以,只要一个与非门,就可以完成所有的逻辑运算。
p33: 掩码是位运算的重要应用,对特定位可以置一,可以清零
p38: 要用C99中的"long long"类型,编译是要用 gcc -std=c99
p39: 补码的利用寄存器的长度是固定的特性简化数学运算。想想钟表,12-1 等价于 12 + 11,利用补码可以把数学运算统一成加法,只要一个加法器就可以实现所有的数学运算。
p44: 注意C语言中有符号数和无符号数的转换规则,位向量不变。想想第一章说的 信息就是"位+上下文"
p48: 怎么样让负数等于正数? 信息安全的逆向思维
p49: 0扩展和符号扩展
p52: 深入思考一下代码和结果
p54: 如何让整数运算溢出?如何避免?
p62例子看看
p67: 关于整数运算的最后思考
p67: 浮点数有科学计数法的基础就不难理解,IEEE标准754
p68: 浮点数运算的不精确性与舍入
p70: IEEE浮点标准,float/double类型
p74: 整数与浮点数表示同一个数字的关系
p78: 整数与浮点数转换规则
p80:家庭作业可以选做,协调好每题最多两人一组做,一星题目一人加一分,二星加二分,三星加三分,四星加四分
笔记:
1.三种数字:无符号数、有符号数(2进制补码)、浮点数,信息安全系同学从逆向角度考虑为什么会产生漏洞
无符号数:基于传统的二进制表示法,表示大于或者等于零的数字。
补码:表示有符号整数最常见的方法,可以为正可以为负。
浮点数:表示实数的科学计数法。
结果太大可能会使得某些运算溢出,大量的计算机安全漏洞是由于计算机算术运算的微妙细节引发的。
2. 进制转换,注意拿二进制作中间结果就好转了
四位二进制等于一位十六进制,2的n次幂换算十六进制,
练习题2.4:
0x503c+0x8=0x5044
0x503c-0x40=0x4ffc
0x503c+64=0x507c
0x50ea-0x503c=0xae
3. gcc -m32 可以在64位机上生成32位的代码
4. 字节顺序是网络编程的基础,记住小端是"高对高、低对低",大端与之相反就可以了。
小端法:最低有效字节在最前面的方式
大端法:最高有效字节在最前面的方式
也有双端法。
已知,Linux 32、 Windows、Linux 64是小端法机器。Sun是大端法机器。
5. p28的代码,使用强制类型转换来访问和打印不同程序对象的字节表示。
代码如下:


执行一下,达到如下结果:

练习2.6:
A:0000 0000 0011 0101 1001 0001 0000 0001
0100 1010 0101 0110 0100 0101 0000 0100
B:右移两位可最大又21位匹配
C:除了最高有效位1,整数的所有位都嵌在浮点数中,而浮点数有一些非零的高位不与整数中的高位相匹配
6. 能区分逻辑运算(结果是1或0)和位运算(结果是位向量),所有逻辑运算都可以用与、或、非表达(最大式、最小式),而与或非可以用"与非"或"或非"表达,所以,只要一个与非门,就可以完成所有的逻辑运算。使用掩码,利用位向量来对集合编码。掩码是位运算的重要应用,对特定位可以置一,可以清零。
练习2.8:
a 01101001
b 01010101
~a 10010110
~b 10101010
a&b 01000001
a|b 01111101
a^b 00111100
7. 要用C99中的"long long"类型,编译是要用 gcc -std=c99,C语言定义了每种数据类型必须能够表示的最小的取值范围。C和C++都支持有符号和无符号数,JAVA只支持有符号数。
练习2.11:
- k
- 此时first=last=3,所以a[3]^a[3]=0
- 第4行修改成first<last即自己不需要与本身交换
练习2.13:
bis(x,y)
bis(bic(x,y),bic(y,x))
bis(x,y)其实是保留x的1,加入了y的1,也就是"或"。
练习2.14:
x&y 0x20 x&&y 0x01
x|y 0x7F x||y 0x01
~x|~y 0xDF !x||!y 0x00
X&!y 0x00 x&&~y 0x01
8. 补码的利用寄存器的长度是固定的特性简化数学运算。类似于钟表,12-1 等价于 12 + 11,利用补码可以把数学运算统一成加法,只要一个加法器就可以实现所有的数学运算。对于某些程序来说,用某个确定大小的表示来编码数据类型非常重要,比如Java标准非常明确,采用补码表示,单字节数据类型成为byte而不是char且没有long long数据类型。因此保证了Java程序在无论什么机器上都能表现得一样。
9. 有符号数还有两种标准的表示方法:反码和原码。C语言允许在各种不同的数字数据类型之间做强制类型转换,且支持所有整型数据类型的有符号和无符号运算,通常大多数数字都默认为有符号的。注意C语言中有符号数和无符号数的转换规则,位向量不变。信息就是"位+上下文"。
练习2.18:
A:440 B:20 C:-424 D:-396 E:68 F:-312 G:16 H:12 I:-276 J:32
练习2.19:
x | hex(x) | T2U4(x) |
-8 | 0x8 | 8 |
-3 | 0xD | 13 |
-2 | 0xE | 14 |
-1 | 0xF | 15 |
0 | 0x0 | 0 |
5 | 0x5 | 5 |
10.怎么样让负数等于正数? 信息安全的逆向思维
利用printf首先将一个字当做一个无符号数输出,然后再把它当做一个有符号数输出。转换的原则是底层的位表示保持不变。就是应用函数U2TW,将无符号数转换为有符号数。
练习2.21:
类型 | 求值 |
无符号数 | 1 |
有符号数 | 1 |
无符号数 | 0 |
有符号数 | 1 |
无符号数 | 1 |
11. 0扩展和符号扩展
0扩展:将一个无符号数转换为一个更大的数据类型,在表示的开头添加0.
符号扩展:将一个补码数字转换为一个更大的数据类型。
练习2.23:
A:fun1是无符号移位,即逻辑移位,fun2则是算数移位
W | fun1(w) | fun2(w) |
0x00000076 | 0x00000076 | 0x00000076 |
0x87654321 | 0x00000021 | 0x00000021 |
0x000000C9 | 0x000000C9 | 0xFFFFFFFC9 |
0xEDCBA987 | 0x00000087 | 0xFFFFFFF87 |
B:fun1从参数的低8位中提取得到范围0-255之间的整数,fun2也是从低8位提取,但是进行了符号扩展,所以是介于-128~127
12. 深入思考一下代码和结果
当参数length为0时,程序代码会出错,说明从有符号数到无符号数的隐式强制类型转换很容易引发错误。由于length在代码中是无符号的,0-1将会进行无符号计算,就会等价于MOD算法,相当于得到一个MAX数值,所以所有数都是小于等于MAX值的,于是总是为真。所以代码尝试访问数组a的非法元素。
练习2.24:
无符号截断值 | 补码截断值 |
0 | 0 |
2 | 2 |
1 | 1 |
3 | 3 |
7 | -1 |
练习2.25:
出错原因:当参数length为0时,程序代码会出错,说明从有符号数到无符号数的隐式强制类型转换很容易引发错误。由于length在代码中是无符号的,0-1将会进行无符号计算,就会等价于MOD算法,相当于得到一个MAX数值,所以所有数都是小于等于MAX值的,于是总是为真。所以代码尝试访问数组a的非法元素。
修改办法:将length声明为int类型进行有符号运算,或者将for循环的测试条件改为i<length防止溢出
13. p54: 如何让整数运算溢出?如何避免?
首先,无符号数运算:所有无符号数运算都是以2的n次方为模,(n是结果中的位数)。所以它不存在运算时的没有那种所谓的"溢出",当它超过范围时,从零开始重新计数!当一个无符号数和有符号数相加的时候,有符号数会自动转化为无符号数参与运算!
其次,有符号数运算: 是可能发生"溢出"的,而且溢出的结果是未定义的。当一个运算的结果发生溢出时,做出任何假设都是不安全的。
避免方法:检查 cpu 的状态标志寄存器中的溢出标志位,验算运算是否超出了溢出标志位。
练习2.27:
int fun(unsigned x,unsigned y){
unsigned sum=x+y;
return sum>=x;
}
练习2.29:
x | y | x+y | x+(t/5)y | 情况 |
[10100] | [10001] | 100101 | 00101 | 1 |
[11000] | [11000] | 110000 | 10000 | 2 |
[10111] | [01000] | 111111 | 11111 | 2 |
[00010] | [00101] | 000111 | 00111 | 3 |
[01100] | [00100] | 010000 | 10000 | 4 |
练习2.33:
x | -(t/4)x | ||
十六进制 | 十进制 | 十进制 | 十六进制 |
0 | 0 | 0 | 0 |
5 | 5 | -5 | B |
8 | -8 | -8 | 8 |
D | -3 | 3 | 3 |
F | -1 | 1 | 1 |
练习2.34:
x·y | 截断的x·y |
20[010100] 12[001100] | 4[100] -4[100] |
14[001110] -2[111110] | 6[110] -2[110] |
36[100100] 4[000100] | 4[100] -4[100] |
14. p62 XDR库中的安全漏洞
参数过大,第10行上的乘法运算会溢出,从第16行开始的循环会试图复制所有字节,超出已分配的缓冲区的界限,从而破坏其他的数据结构,导致程序崩溃或者行为异常。可见malloc使用了一个32位无符号数作为参数,因此不可能分配一个大于232个字节的块,所以没必要,应该将其放弃,返回一个NULL。
练习2.39:
将表达式变为-(x<<m),设字长w,n=w-1。计算(x<<w)-(x<<m),而将x向左移动w位会得到0。
练习2.40:
表达式 |
(x<<2)+(x<<1) |
(x<<5)-x |
(x<<1)-(x<<3) |
(x<<6)-(x<<3)-x |
练习2.42:
int div16(int x){
int bias=(x>>31)&0xF;
return (x+bias)>>4;
}
练习2.43:
M=31,利用(x<<5)-x求x*M
N=8,y是负数时加上偏置量7,且右移3位
15.关于整数运算的最后思考
计算机执行的"整数"运算实际上是一种MOD运算形式,表示数字的有限字长限制了可能的值的取值范围,导致运算结果溢出。补码提供了一种既能表示负数又能表示整数的灵活方法。C语言中某些规定可能会产生出乎意料的结果,而且难以察觉,unsigned
数据类型概念上简单,却可能导致很多意想不到的行为。
练习2.44:
A:假。令x=TMin32,x-1=TMax32
B:真。前式为0则有位x2等于1,左移29位后,x2将会成为符号位
C:假。令x为0xFFFF,x*x为0xFFFE0001.
D:真。X非负数,-x是非正。
E:假。令x=TMin32,那么x与-x都是负数
F:真。
G:真。~y=-y-1.uy*ux=x*y,所以等价。
16. 浮点数有科学计数法的基础就不难理解,IEEE标准754
17.浮点数运算的不精确性与舍入
二进制表示法只能表示那些能够被写成x*2y的数,其它的值只能被近似表示。增加二进制的表示长度可以提高表示的精度。
练习2.45:
小数值 | 二进制表示 | 十进制表示 |
1/8 | 0.001 | 0.125 |
3/4 | 0.11 | 0.75 |
25/16 | 1.1001 | 1.5625 |
43/16 | 10.1011 | 2.6875 |
9/8 | 1.001 | 1.125 |
47/8 | 101.111 | 5.875 |
51/16 | 11.0011 | 3.1875 |
18. IEEE浮点标准,float/double类型
IEEE浮点标准用V=(-1)S*M*2E的形式来表示一个数:符号s决定正负,对于数值0的符号位解释作为特殊情况处理。尾数M是一个二进制小数。阶码E作用是对浮点数加权,权重是2的E次幂。
浮点数的位划分三个字段,分别对这些值进行编码:
一个单独的符号位s直接编码符号s
K位的阶码字段编码阶段E
N位小数字段编码尾数M
两种最常见的格式就是float 和double,区分一下单精度和双精度的具体情况。
练习2.47:
见书本。
19.整数与浮点数表示同一个数字的关系:相关的区域对应整数的低位,刚好在等于1的最高有效位之前停止,也就是隐含的开头的位1,与浮点数表示的小数部分的高位时相匹配的。
练习2.50:
原始值 | 舍入后的值 |
10.0102 2+(1/4) | 10.0 2 |
10.0112 2+(3/8) | 10.1 2+(1/2) |
10.1102 2+(3/4) | 11.0 3 |
11.0012 3+(1/8) | 11.0 3 |
练习2.52:
1011110 | 15/2 | 1001111 | 15/2 |
0101001 | 25/32 | 0110100 | 3/4 |
1101111 | 31/2 | 1011000 | 16 |
0000001 | 1/64 | 0001000 | 1/64 |
20.整数与浮点数转换规则
- 从int转换成float,数字不会溢出但是可能被舍入。
- 从int或者float转换成double,能保留足够精确的数值
- 从double转换成float,可能溢出成正无穷或负无穷,由于精确度较小,还可能被舍入
- 从float或者double转化成int,值会向零舍入,也就是可能溢出。一个浮点数向整数转换,如果不能为该浮点数找到一个合理的整数近似值,就会产生整数不确定值。
练习2.54:
A:真,double比int具有更大的精度和范围
B:假,令x=TMax即为假
C:假,令d=le40,右边可得到正无穷
D:真,double比float具有更大的精度和范围
E:真,浮点数取非就是对他的符号位取反
F:真,这是浮点数的除法
G:真
H:假,令f为1.0e20而d为1.0,f+d会舍入到1.0e20,左式因此求得0.0而右式为1.0。
家庭作业:
2.65 写出代码实现如下函数:
/*Return 1 when x contains an even number of 1s; 0 otherwise. Assume w=32*/
int even_ones(unsigned x);
函数应该遵循位级整数编码规则,不过你可以假设数据类型int有w=32位,你的代码最多只能包含12个算术运算、位运算和逻辑运算。
解读题目:当无符号数x包含偶数个1时,返回值为1,否则为返回值为0,假设x的数据类型是int 有w=32位。
解题思路:要求x所包含的1的个数,可以对x的每个位进行异或运算。如果得到的结果是0,那么就说明x包含偶数个1,则返回值为1,;如果得到的结果是1,那么说明x包含奇数个1,则返回值为0。
代码编写过程:由于x是个32位int类型数,所以①首先采用折半缩小规模的方法进行逐位异或。②最后得到的x值再与1进行与运算就会得到一个32位中前31均为0,尾数是0或者是1(用于判断是原x包含奇数还是偶数个1),③返回这个值就完成了题目需求。
代码编写:
int even_ones(unsigned x){
x ^= (x >> 16);//等同于x=x^(x>>16)
x ^= (x >> 8); //等同于x=x^(x>>8)
x ^= (x >> 4); //等同于x=x^(x>>4)
x ^= (x >> 2); //等同于x=x^(x>>2)
x ^= (x >> 1); //等同于x=x^(x>>1)
return !(x&1);
}
遇到的问题及解决:
- 一开始对算数移位和逻辑移位混淆,不知道在右移的时候应该补1还是0。
解决:在相似的重复的练习中摸清楚了算数移位是需要补1而逻辑移位需要补0
- 在练习2.13中遇到的两个几乎陌生的函数bis和bic,仅用两个陌生的函数就可以做到or和xor的功能让我无所适从。
解决:我在草稿纸上根据bis和bic的功能假设了两个8位二进制数,通过bis和bic
的运算来摸清他们之间的规律。
- 对于计算机计算"整数"的MOD算法其实是抱有疑惑,不能很好地判断到底是什么时候会溢出,使得数据结构损坏。
解决:只好通过做几道练习题来稍稍了解。
- 家庭作业中,一开始就懵逼了,题目很简单,但是做起来缺没用想象中那么容易,因为我只是隐约记得以前在C语言中好像学过是有通过位运算来判定所包含的1或者0的个数。
解决:经过搭档符运锦同学给我的题目解析和解题思路,我根据逐位异或的算法把这道家庭作业的代码写了出来。截图:
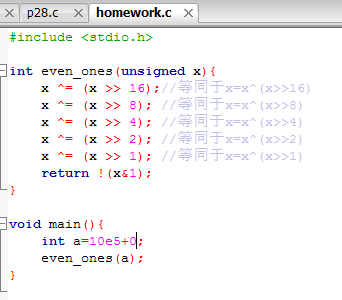
结果:

即当a为10e5+0时,返回值为0
若a为10e5+1时,返回值为1





