某科学的PID算法学习笔记
PID算法应用广泛，比如加热器、平衡车、无人机等等，是自动控制理论中比较容易理解但十分重要的算法。本篇笔记详细记录了PID算法推导过程，并针对无人机姿态调整问题进行了简单分析和仿真，文末提供4种编程语言（C， C++， Python, Matlab）仿真源码。
最近，在某社团的要求下，自学了PID算法。学完后，深切地感受到PID算法之强大。PID算法应用广泛，比如加热器、平衡车、无人机等等，是自动控制理论中比较容易理解但十分重要的算法。
下面是博主学习过程中所做的笔记，笔记后面提供了4种编程语言的仿真代码（C, C++, Python, Matlab)，使实现方式更加灵活，同时增强对PID的理解。(文章较长，可点击右侧目录选择性阅读）
PID算法学习笔记
参考：PID基础入门教程
一、位式控制算法
1.1 位式控制算法原理
位式控制算法，通过比较SV(设定值)和PV(当前值)，输出高低电平给执行部件，执行部件（如开关）通过执行/停止来控制目标（如加热器），控制对象通过传感器将当前值反馈给控制算法，如图1。
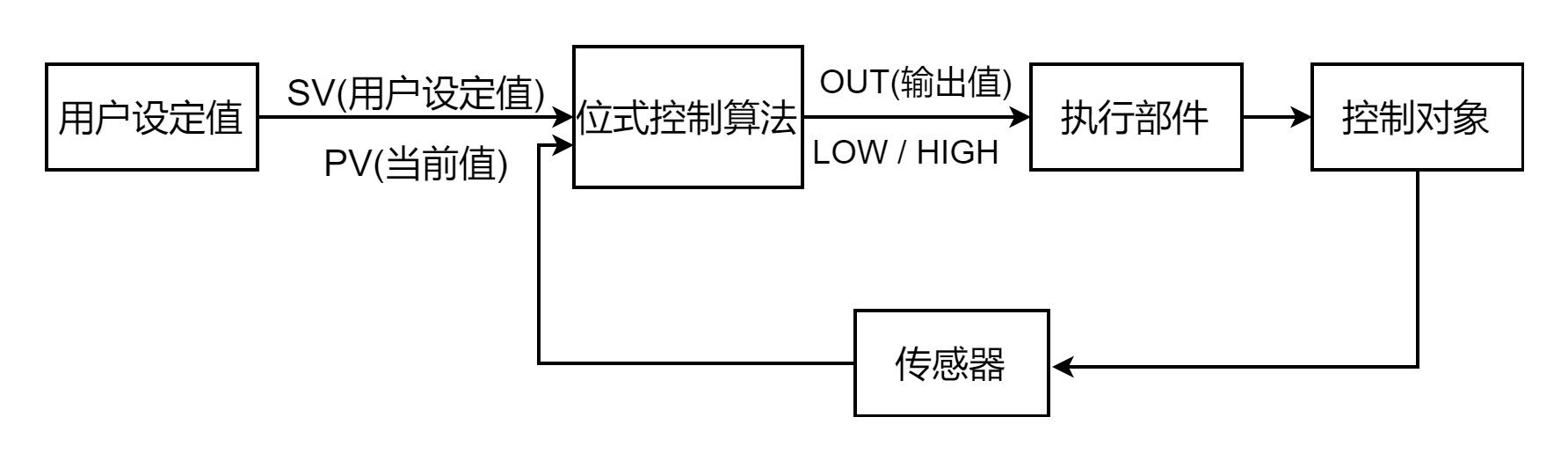
图1 位式控制算法简单应用
1.2 位式控制算法特点
位式控制算法具有如下特点：
（1）输出信号一般只有两种状态(LOW / HIGH)。
（2）通过比较SV和PV的值来产生OUT值，比如PV < SV输出高电平，PV > SV输出低电平。
（3）只比较控制对当前的状态值。
1.3 位式控制算法缺陷
位式控制算法的缺陷：
（1）输出信号单一，缺乏包容性。
（2）仅仅活在当下，没有回顾历史和展望未来。
二、PID控制算法
2.1 PID算法原理
PID控制算法，通过分析PV与SV的偏差值（包括当前偏差、历史偏差、最近偏差），输出值（PWM）经过执行器转换后应用于控制对象，控制对象通过传感器将PV反馈给PID，通过硬件寄存器等记录偏差值，以便PID随时调用，如图2。
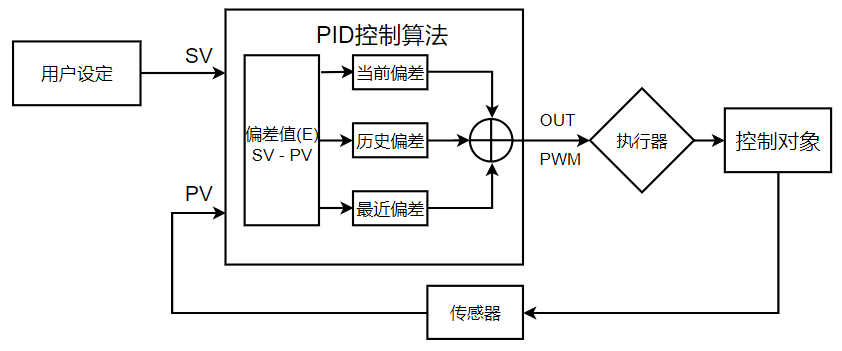
图2 PID控制算法简单应用
假设从“0”时刻到 k 时刻，传感器获取的状态值分别为
${X_{0}, X_{1}, X_{2}, ..., X_{k-1}, X_{k}}$
2.2 PID比例控制
在2.1的条件下，设偏差值 Ek 为设定值与当前值之差，即
${E_{k}=SV-X_{k}}$
实际应用中的偏差值存在如下3种情况
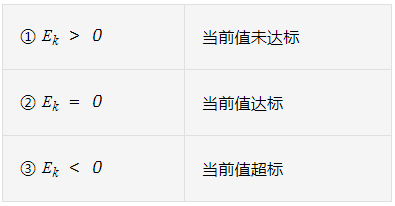
分析以上三种情况，不同情况下算法将输出不同值。比如算法在Ek > 0时输出较高的值，以促进当前值接近设定值。而实际应用中，控制对象的状态偏差值一般不能直接作为PWM输出值，需要进行一定比例的放大或缩小，以提高控制灵敏度。因此输出值满足关系式
${P_{out}=K_{p}\cdot E_{k}+OUT_{0}}$ ①
其中，POUT为输出值，一般与PWM有关。Kp 为比例系数，对偏差值Ek 进行一定比例的放大或缩小。OUT0 是当偏差值为 0 时，算法的输出值，防止负载失控。分析公式可知，偏差值Ek 越大，输出值越大，当前值接近设定值的速度越快，当前值超过设定值时，Ek < 0, 算法输出负值，当前值减小。往复循环，直到当前值稳定在设定值的误差允许范围内。
2.3 PID积分控制
在2.2的条件下，将历史偏差相加，其和为
${S_{k}=E_{0}+E{1}+E_{2}+...+E_{k-1}+E_{k}}$
实际应用中的历史偏差值之和存在如下3种情况
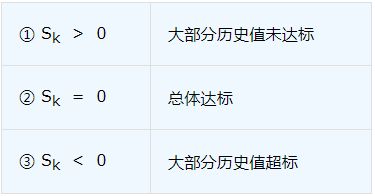
不同情况下输出值应不同，分析以上情况，可以令输出值满足关系式
${I_{out}=K_{p}\cdot S_{k}+OUT_{0}}$ ②
其中Iout为输出值，Kp为比例系数，Sk为历史偏差和，OUT0为初始值。通过上述算法，可以对控制对象的历史状态值进行评估，根据历史状态判断输出值的大小。这种方法比较局限，因为当历史值较多时，当前值的变化将很难引起输出值改变，因此积分控制一般不会从0开始启动，当当前值接近设定值时才开启积分控制，以减少参考的历史值。
2.4 PID微分控制
在2.2的条件下，将最近两次偏差值相减，其差为
${D_{k}=E_{k}-E_{k-1}}$
实际应用中的最近偏差值之差存在如下3种情况
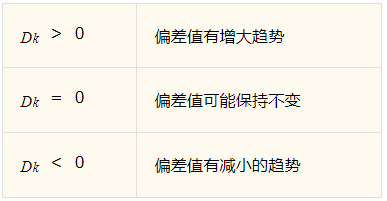
不同情况下输出值应不同，分析以上情况，可以令输出值满足关系式
${D_{out}=K_{p}\cdot D_{k}+OUT_{0}}$ ③
其中Dout为输出值，Kp为比例系数，Sk为历史偏差和，OUT0为初始值。通过最近偏差值之差，判断偏差值的变化趋势，预测未来的偏差值大小，从而输出对应的PWM。
2.5 PID算法模型
根据以上分析，每种控制算法均有较大局限。因此综合①②③算法，令输出值为
${PID_{out_{k}}=P_{out}+I_{out}+D_{out}}$
代入①②③关系式，并进行简单归并，得到关系式
${PID_{out_{k}}=K_{p}\cdot \left ( E_{k}+S_{k}+D_{k}\right )+OUT_{0}}$ ④
分析上式中 Sk , Dk 的值，假设T为计算周期，即每次运行算法的时间间隔，Ti为积分时间常数，用于控制积分算法对输出值的影响因数，Td为微分时间常数，用于控制微分算法对输出值的影响。
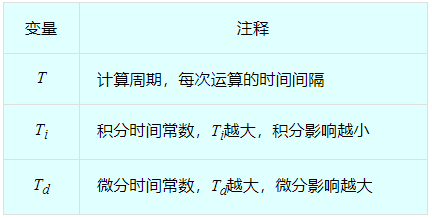
综上，积分控制Sk满足关系式
${S_{k}=\frac{1}{T_{i}}\cdot\sum_{k=0}^{k}E_{k} \cdot T}$ ⑤
微分控制Dk满足关系式
${D_{k}=T_{d}\cdot\frac{\left ( E_{k}-E_{k-1}\right )}{T}}$ ⑥
综合④⑤⑥，并进行简单的归并处理后，得到PID的输出关系式
${PID_{out_{k}}=P\left (K_{p}\cdot E_{k} \right )+I\left (K_{p}\cdot \frac{T}{T_{i}}\cdot \sum_{k=0}^{k}\cdot E_{k} \right )+D\left [K_{p}\cdot \frac{T_{d}}{T}\cdot\left(E_{k}-E_{k-1}\right) \right ]}$ ⑦
其中P，I，D分别表示比例，积分，微分控制。通过调整 Kp ，Ti ，Td 的值来调整P， I，D对输出值的影响权重，从而使当前值更快接近并稳定在设定值误差允许范围内。
上述算法有一个明显的特点，即计算结果输出为PWM值，直接控制负载。因此又被称为“位置式PID算法“
2.6 增量式PID算法
实际应用中，大部分控制系统具有记忆功能，可以记录每个时刻状态值，因此为了减小累加产生的运算负担，可以采用计算“增量”的方式来输出控制信号。
增量式PID算法的特点是只计算增加（减小）值，历史值加上增加值即为输出值，满足关系式
${\Delta PID_{out}=PID_{out_{k}}-PID_{out_{k-1}}}$ ⑧
代入④关系式，
${\Delta PID_{out}=P\left [K_{p}\cdot \left ( E_{k}-E_{k-1}\right ) \right ]+I\left (K_{p}\cdot \frac{T}{T_{i}}\cdot E_{k} \right )+D\left [K_{p}\cdot \frac{T_{d}}{T}\cdot \left ( E_{k}-2E_{k-1}-E_{k-2}\right ) \right ]}$ ⑨
对比⑧式和⑦式，⑧式运算量更小。因此对于有记忆功能的硬件系统，可以使用增量式PID算法，以减少运算，提升性能。
PID仿真实验
一、问题
既然是仿真实验，那就应该以模拟解决生活中的问题为主，为了进行比较具体，但不复杂的仿真实验，博主绞尽脑汁，终于构造了下面这个题目。
在《机甲大师》动漫中，主角“单单”拥有一架语音遥控的双旋翼无人机，名叫“KAKA"。如图1，动漫第一集5:35左右，KAKA在追踪飞盘时，突然受海风影响，飞行姿态偏离水平位置。性能超高的KAKA通过内部传感器测得偏角后，迅速调整姿态，恢复水平。请对这一情形进行建模分析。
图1 被海风影响的KAKA
二、解答
分析题目，需要对KAKA“恢复姿态”这一现象进行分析。围绕这个问题，下面以“建立物理模型→建立数学模型→算法仿真”进行逐步分析。
2.1 建立物理模型
首先简化问题，将KAKA看作刚性直杆。如图2.1，一质量为2m，长度为2r的刚性直杆，两端垂直固定一个不计质量的直流电机。直杆可以绕中心自由旋转，初始位置相对水平线偏离θ角。
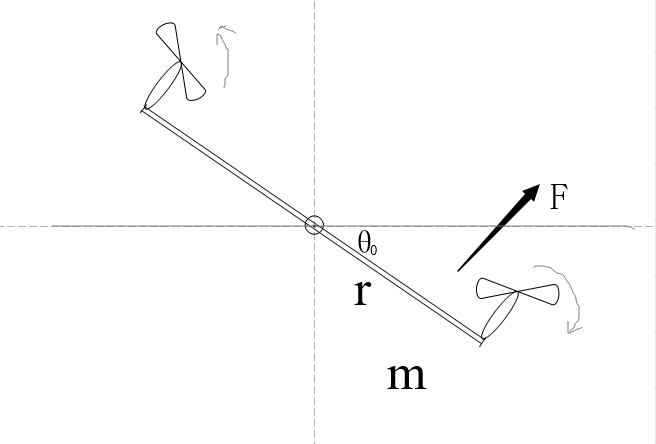
为了使直杆恢复水平位置，改变右端电机转速，产生“额外”升力F。
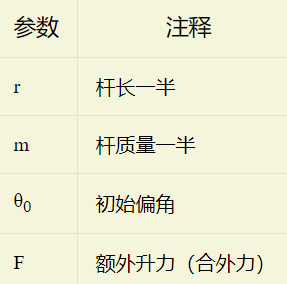
根据以上参数，在理想情况下，可以得到直杆的合外力矩M满足
${M = F\cdot r}$ ①
转动惯量J满足
${J=\frac{2}{3}mr^{2}}$ ②
由刚体轴转动定理
${M=J\cdot \alpha}$ ③
其中α为角加速度，满足关系式
${\alpha =\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}}$ ④
其中t为时间，联立①②③④，求解微分方程可得到关系式
${\theta _{t}=\frac{3\cdot F}{4\cdot m\cdot r}\cdot t^2}$ ⑤
其中θ为直杆在力合外力F的作用下，经过时间t后转动的角度。
2.2 建立数学模型
设${T}$为计算周期，在⑤式的条件下，令${t=T}$，在${T}$时间内直杆转动角度满足关系式
${\theta _{T} =\frac{3\cdot F}{4\cdot m\cdot r}\cdot T^2}$ ⑥
假设${F}$随时间的变化周期为${T}$，那么经过${t}$时间后，${F}$变化${n}$次，直杆转动角度满足
${\theta =\frac{3\cdot T^2}{4\cdot m\cdot r}\cdot\sum_{n=0}^{n} F_{n}}$ ⑦
直杆与水平线的当前偏差角${E_{k}}$满足
${E_{k}=\theta_{0}-\frac{3\cdot T^2}{4\cdot m\cdot r}\cdot\sum_{n=0}^{k} F_{n}}$ ⑧
上式即为直杆在恢复水平位置过程中，在合外力F作用下，当前偏角对于时间的函数。
参考实际情况，由于合外力以T为周期发生变化，该偏角函数曲线应如满足图2.2
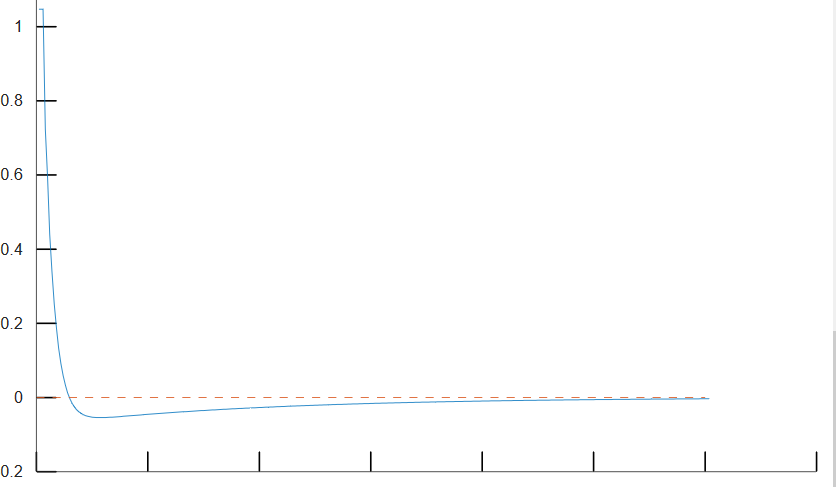
图2.2 （预测）直杆偏角对于时间的变化曲线
分析上图曲线，发现其变化趋势可以用PID算法进行拟合。
2.3 PID算法仿真
分析关系式⑧，其中${T}$可以看作采样周期，${F}$为算法输出值，${E_{k}}$为当前偏差角。应用位置式${PID}$算法，设比例系数为${K_{p}}$，积分时间常数为${T_{i}}$，微分时间常数为${T_{d}}$，输出值满足PID算法关系式
${F_{out_{k}}=K_{p}\cdot E_{k} +K_{p}\cdot \frac{T}{T_{i}}\cdot \sum_{k=0}^{k}\cdot E_{k} + K_{p}\cdot \frac{T_{d}}{T}\cdot E_{k}-E_{k-1}}$ ⑨
分析⑧式，为了简化计算，不妨令
${m = 0.3}$, ${r=0.1}$, ${\theta _{0}=\frac{\pi}{3}}$ （${SI}$）
则当前偏差角满足
${E_{k}=\frac{\pi}{3}-25\cdot T^2\cdot\sum_{n=0}^{k} F_{out_{n}}}$ ⑩
综上，可以假设如表2.3中的参数
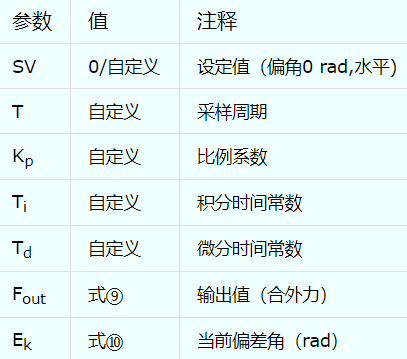
表2.3 PID参数
下面，在上述模型条件下，用5种编程语言(Matlab, C, C++, Python)进行算法仿真。
1) Matlab
比较方便，可以先通过Matlb仿真确定PID系数
源码：
clear,clc,close all % 清屏
syms x
SV = 0; % 设定值，角（弧）度 0 (rad)
T = 0.01; % 计算周期/采样周期
Kp = 50; % 比例系数
Ti = 5; % 积分时间常数
Td = 0.05; % 微分时间常数
E = []; % 历史偏差
Fout = []; % 输出值，升力
E(1) = pi ./3; % 初始角度 π/3 (rad)
for i = 1:1:3 % 绘制3种比较曲线
if i == 2;
Kp = 50; % 比例系数
Ti = 0.05; % 积分时间常数
Td = 0.05; % 微分时间常数
E = []; % 历史偏差
Fout = []; % 输出值，升力
E(1) = pi ./3; % 初始角度 π/3 (rad)
end % if i ==2
if i ==3;
Kp = 50; % 比例系数
Ti = 5; % 积分时间常数
Td = 0.005; % 微分时间常数
E = []; % 历史偏差
Fout = []; % 输出值，升力
E(1) = pi ./3; % 初始角度 π/3 (rad)
end % if i ==3
for t = 0:0.01:3; % 计算300次
k = round(t*100 + 2); % 当前指数
E(k) = E(1) - 25*(T^2)*sum(Fout); % 获取当前值
%#### 核心，PID计算输出值 ####%
if k>2;
if E(k) != 0;
Fout(k) = Kp*(E(k) + (T./Ti)*sum(E) + (Td./T)*(E(k)-E(k-1)));
end % end if E(k) !=0
end % end if k>2
%#############################%
k++; % 当前指数+1
end % end for 计算400次
hold on
plot(E) % 显示数据图
end % for 绘制3种比较曲线
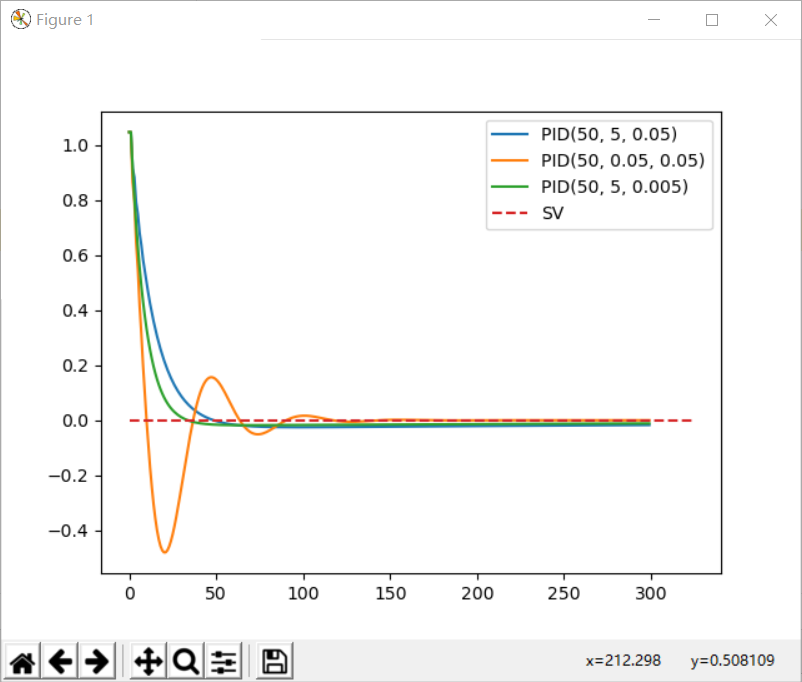
legend('PID(50, 5, 0.05)','PID(50, 0.05, 0.05)','PID(20, 5, 0.005)')
hold on
plot([0,300],[0,0],'--'); % 显示参考线，斜率0，截距0
运行结果
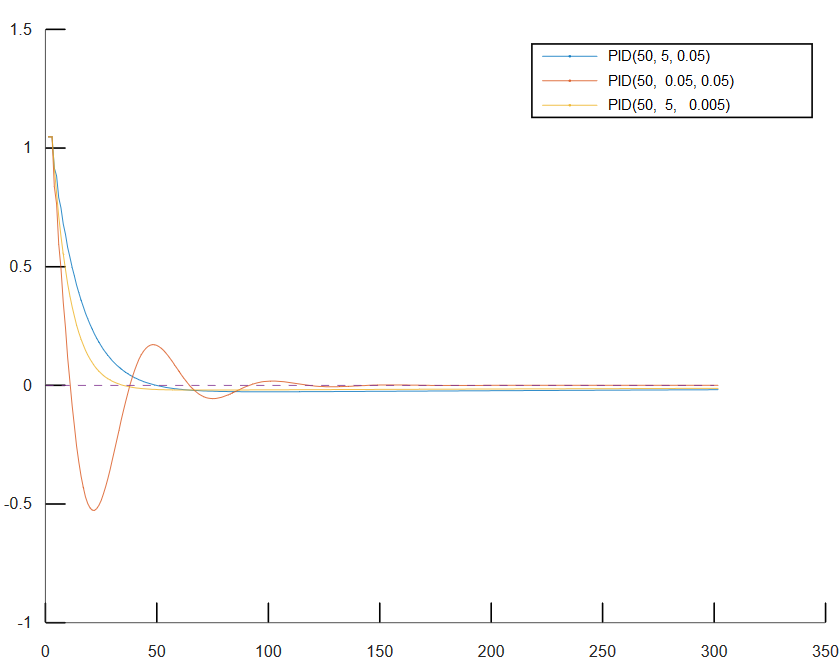
2) C语言
1 /**@file main.c 2 * @brief 位置式PID C语言算法仿真 3 * @author BROSY 4 * @copyright CSU | BROSY 5 ********************************************************************************/ 6 7 8 /************************************************************************************* 9 注：以便查阅，我将所有函数和声明都放在main.c中，进行项目实践时，再设计文件架构 10 *************************************************************************************/ 11 12 13 #include<stdio.h> 14 #define PI (3.1416) 15 16 typedef struct { 17 const int SV = 0; // 设定值（弧度rad) 18 19 double InitVal; //初始偏差值 20 double T; // 采样周期 21 double Kp; // 比例系数 22 double Ti; // 积分时间常数 23 double Td; // 微分时间常数 24 double Ek; //当前偏差 25 double SumEk; //历史偏差之和 26 double Ek_1; //上次偏差 27 double SumFout; // 输出值之和 28 }PID_Structure; 29 30 /** 31 @brief 位置式PID输出函数 32 @param [in] PID结构体 33 @return 算法输出值（额外升力） 34 */ 35 double PID_OUT(PID_Structure* PID) 36 { 37 double Fout; 38 Fout = PID->Kp * (PID->Ek 39 + (PID->T / PID->Ti) * PID->SumEk 40 + (PID->Td / PID->T) * (PID->Ek - PID->Ek_1)); 41 42 return Fout; // 输出值（额外升力） 43 } 44 45 46 /** 47 @brief 获取当前偏差值 48 @param [in] PID结构体, 历史输出值（数组） 49 @return kaka当前状态偏差值 50 */ 51 double GetCurrE(PID_Structure PID) 52 { 53 double Ek; 54 Ek = PID.InitVal - 25 * (PID.T * PID.T) * PID.SumFout; 55 return Ek; 56 } 57 58 int main() 59 { 60 PID_Structure PID; // 创建PID 61 62 PID.InitVal = PI / 3; 63 PID.T = 0.01; 64 PID.Kp = 50; 65 PID.Ti = 5; 66 PID.Td = 0.005; 67 PID.Ek = 0; 68 PID.Ek_1 = 0; 69 PID.SumFout = 0; 70 PID.SumEk = 0; 71 72 // 计算400次 73 for (int i = 0; i < 400; i++) 74 { 75 if (i > 0) 76 { 77 PID.Ek_1 = PID.Ek; // 获取k-1的偏差值 78 } 79 PID.Ek = GetCurrE(PID); // 获取当前偏差值 80 PID.SumEk += PID.Ek; // 历史偏差之和 81 82 printf("%f\n", PID.Ek); 83 if (PID.Ek != 0 && i > 0) // 误差 84 { 85 PID.SumFout += PID_OUT(&PID); // 获取输出值之和 86 87 } 88 else 89 { 90 PID.SumFout += 0; // 储存输出值 91 } 92 } 93 94 }
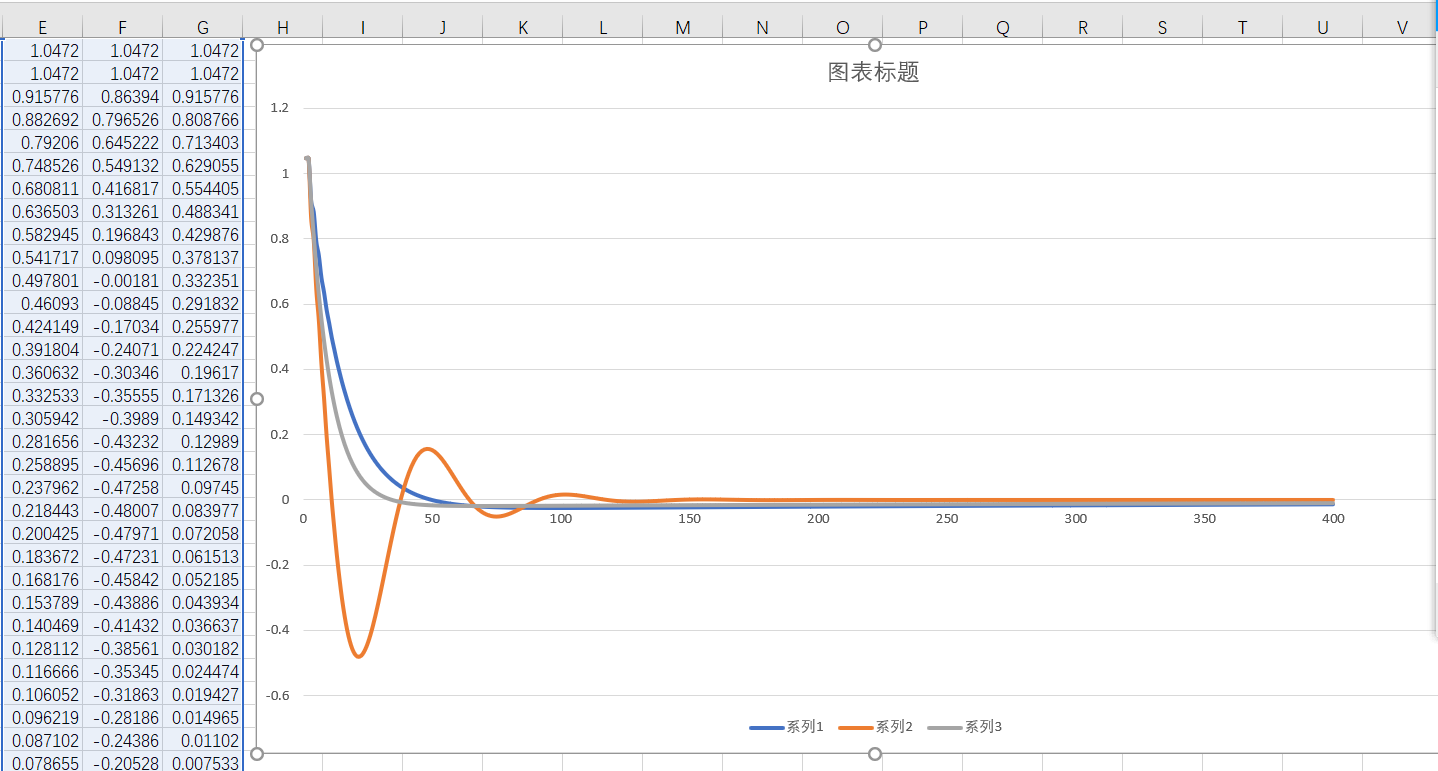
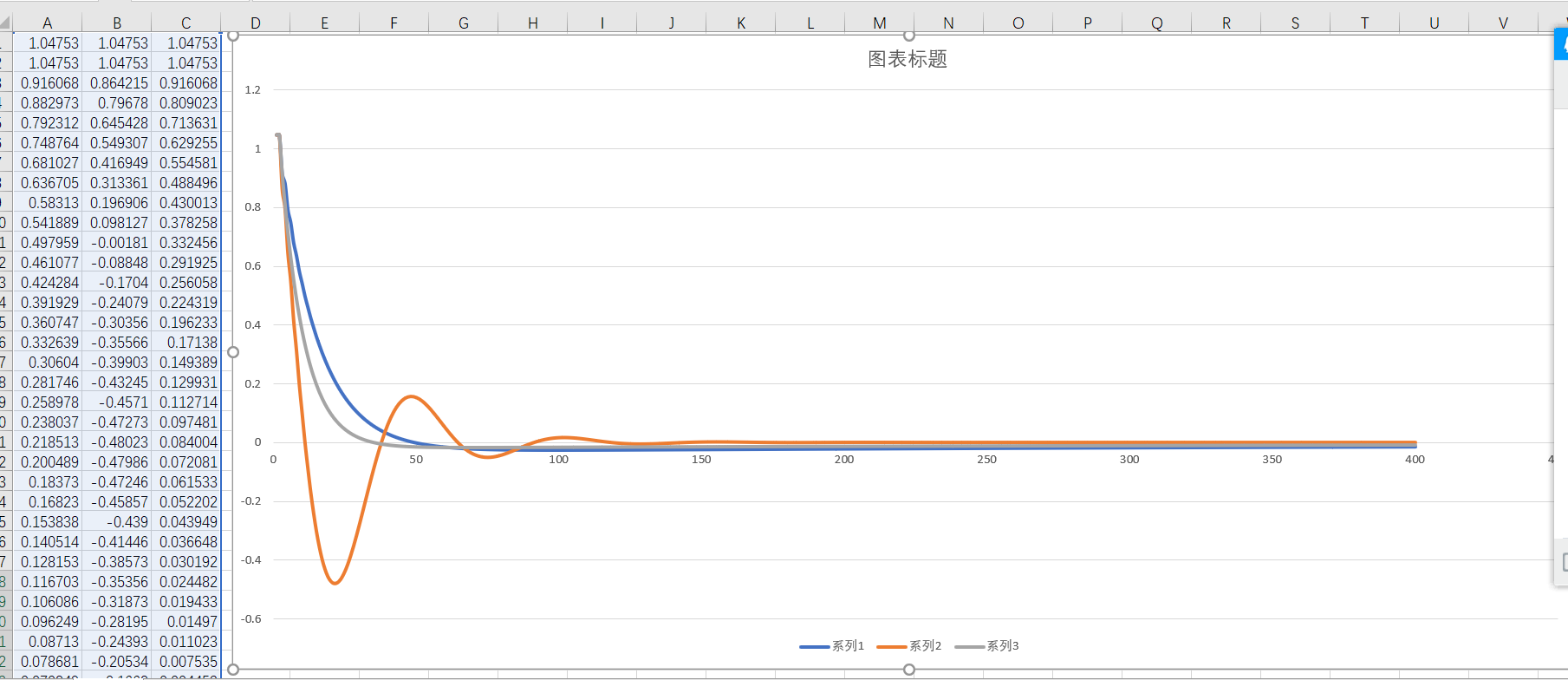
将输出结果导入到excel中并绘制曲线：
3) C++
1 /**@file main.cpp 2 * @brief 位置式PID C语言算法仿真 3 * @author BROSY 4 * @copyright CSU | BROSY 5 ********************************************************************************/ 6 7 #include "PID.h" 8 9 int main() 10 { 11 PID* pid[3]; // 创建PID 12 13 14 pid[0] = new PID(50, 5, 0.05); // 初始化PID1 15 pid[1] = new PID(50, 0.05, 0.05); // 初始化PID2 16 pid[2] = new PID(50, 5, 0.005); // 初始化PID3 17 18 for (int i = 0; i < 3; i++) 19 { 20 pid[i]->Loop(400);// 计算400次 21 delete pid[i]; // 释放内存 22 } 23 }
1 #include "PID.h" 2 #include <iostream> 3 /** 4 @brief 初始化PID参数 5 @param [in] P I D系数 6 只设置P I D的系数，其余默认 7 */ 8 PID::PID(double P, double I, double D) 9 { 10 Kp = P; 11 Ti = I; 12 Td = D; 13 14 InitVal = (3.1426)/3; // 初始偏差值π/3 15 T = 0.01; // 采样周期 16 Ek = 0; //当前偏差 17 SumEk = 0; //历史偏差之和 18 Ek_1 = 0; //上次偏差 19 SumFout = 0; // 输出值之和 20 } 21 22 /** 23 @brief 位置式PID输出函数 24 @return 算法输出值（额外升力） 25 */ 26 double PID::PID_OUT() 27 { 28 double Fout; 29 30 Fout = Kp * (Ek 31 + (T / Ti) * SumEk 32 + (Td / T) * (Ek - Ek_1)); 33 34 return Fout; // 输出值（额外升力） 35 } 36 37 38 /** 39 @brief 获取当前偏差值 40 @return kaka当前状态偏差值 41 */ 42 double PID::GetCurrE() 43 { 44 double Ek; 45 Ek = InitVal - 25 * (T * T) * SumFout; 46 return Ek; 47 } 48 49 /** 50 @brief 循环计算并输出值 51 @param [in] 计算次数 52 */ 53 void PID::Loop(int times) 54 { 55 std::cout << "计算次数：" << times << std::endl; 56 std::cout << "P = " << Kp << std::endl; 57 std::cout << "I = " << Ti << std::endl; 58 std::cout << "D = " << Td << std::endl<<std::endl; 59 60 for (int i = 0; i < times; i++) 61 { 62 if (i > 0) 63 { 64 Ek_1 = Ek; // 获取k-1的偏差值 65 } 66 Ek = GetCurrE(); // 获取当前偏差值 67 SumEk += Ek; // 历史偏差之和 68 69 std::cout << Ek << std::endl; 70 if (Ek != 0 && i > 0) // 误差 71 { 72 SumFout += PID_OUT(); // 获取输出值之和 73 74 } 75 else 76 { 77 SumFout += 0; // 储存输出值 78 } 79 } 80 }
#pragma once class PID { private: const int SV = 0; // 设定值（弧度rad) double InitVal; //初始偏差值 double T; // 采样周期 double Kp; // 比例系数 double Ti; // 积分时间常数 double Td; // 微分时间常数 double Ek; //当前偏差 double SumEk; //历史偏差之和 double Ek_1; //上次偏差 double SumFout; // 输出值之和 public: PID(double P, double I, double D); // PID初始化，只输入PID系数，其余默认 double PID_OUT(); // PID算法核心，计算输出值 double GetCurrE(); // 获取当前值 void Loop(int times); // 循环计算输入计算次数 };
将输出结果导入到excel中并绘制曲线：
4) Python
1 import matplotlib.pyplot as plt # 导入绘图库 2 import numpy as np 3 4 ''' 5 @brief 位置式PID输出函数 6 @param [in] PID结构体 7 @return 算法输出值（额外升力） 8 ''' 9 10 11 def pid_out(): 12 f_out = Kp * (Ek 13 + (T / Ti) * sum_Ek 14 + (Td / T) * (Ek - Ek_1)) 15 return f_out 16 17 18 ''' 19 @brief 获取当前偏差值 20 @param [in] PID结构体, 历史输出值（数组） 21 @return kaka当前状态偏差值 22 ''' 23 24 25 def get_curr_e(): 26 ek = init_val - 25 * (T ** 2) * sum_f_out 27 return ek 28 29 30 sv = 0.0 # 设定值 31 init_val = (3.1416) / 3 # 初始值 32 T = 0.01 # 采样周期 33 times = 300 # 计算次数 34 e = np.zeros(times) 35 for t in range(3): 36 Ek = 0.0 # 当前偏差 37 sum_Ek = 0.0 # 历史偏差之和 38 Ek_1 = 0.0 # 上一次偏差 39 sum_f_out = 0.0 # 输出值之和（升力） 40 41 if t == 0: 42 Kp = 50 # 比例系数 43 Ti = 5 # 积分时间常数 44 Td = 0.05 # 微分时间常数 45 if t == 1: 46 Kp = 50 # 比例系数 47 Ti = 0.05 # 积分时间常数 48 Td = 0.05 # 微分时间常数 49 if t == 2: 50 Kp = 50 # 比例系数 51 Ti = 5 # 积分时间常数 52 Td = 0.005 # 微分时间常数 53 54 ''' 55 @brief 循环计算并输出值 56 @param [in] 计算次数 57 ''' 58 for i in range(times): 59 if i > 0: 60 Ek_1 = Ek 61 62 Ek = get_curr_e() # 获取当前值 63 sum_Ek = sum_Ek + Ek # 获取历史值之和 64 65 e[i] = Ek # 储存当前值，方便后面绘图 66 67 if Ek != 0 and i > 0: 68 sum_f_out = sum_f_out + pid_out() # 获取输出值之和 69 70 plt.plot(e, label='PID({0}, {1}, {2})'.format(Kp, Ti, Td)) # 画曲线图，显示PID图例 71 72 plt.plot(np.zeros(times + 25), label='SV', linestyle='--') # 设定值 73 plt.legend() # 显示图例 74 75 plt.show()
下载源码
链接：PID仿真源码 密码：hhh
