10.21~10.27 总结

联考：https://www.cnblogs.com/british-union/p/liankao.html

做题：学了一下线段树 3，现在可以默写对了。

CSPS2 过程

14：26 发了密码开始看题。先读了一遍，感觉 T1 T2 是简单题，T3 可能得出充分必要条件之后 DS 优化 dp？T4 很长，但是我最讨厌 \(2^k\) 相关题（包含位运算），并瞬间想到之前某次联考的在这个满二叉树上做 dp 套 dp 的史题（注：\(\color{red}{\textbf{N}}\color{black}{\textbf{ityacke}}\) 场切了）。

T1 发现直接从小到大吃能吃的最大的即可？塞进 map 即可。

这里发现小熊猫的史处：Ctrl+Backspace 会删掉一整行，对于我常用 Ctrl+backspace 的很难受。。自动编译显示警告对于我常常写 1<<k-i 也很难受（不过可以查没有返回值的问题！！），但是鉴于 dev 是史史史，没有 VSCODE，所以还是只能小熊猫。

T2 怎么还要分讨，，，题面提示卡精度，但是规避 double 不用写分数类，还行。每个位置分讨之后就是区间必须至少保留一个的问题了。这直接去掉包含别人的区间之后每个位置二分就可以了。这个时候只过了 40 分钟，优势在我（存疑）。

T3 尝试寻找某些位置为 \(1\) 合法的充要条件，然后发现贡献 byd 就只有颜色段内和段两侧，这不是 \(w(l,r)\) 的区间划分问题吗？？一度以为把 aliens 出到 CSPS 来了，还试图使用 LCT 维护，然后发现直接 dp 是线性。然后不知道为什么 70 分钟才通过（旁边的小朋友还在 duel，，）。考场以为优势大完了，之后得知 \(\color{red}{\textbf{N}}\color{black}{\textbf{ityacke}}\) 只花了 40 分钟，十分勇猛。

这个时候看 T4：这个数据范围 byd 是要线性？？

肯定先是建棵树出来，从下到上限制逐渐变严非常好，这使得未确定数成为了万金油：他们可以在任何位置成功或失败。然后树上每个点记录可能获胜者，发现是一些确定数和一个区间的未确定数，一次更新被影响的只有到根的链。显然只有 \(\log\) 个确定数，直接合并得到 \(Tn\log^2n\) 的复杂度，发现能过 64~76。

这玩意和暴力差不多，于是尝试想正解，，我觉得这可能跟到根的类型序列有点小关系，与i是小分讨一下

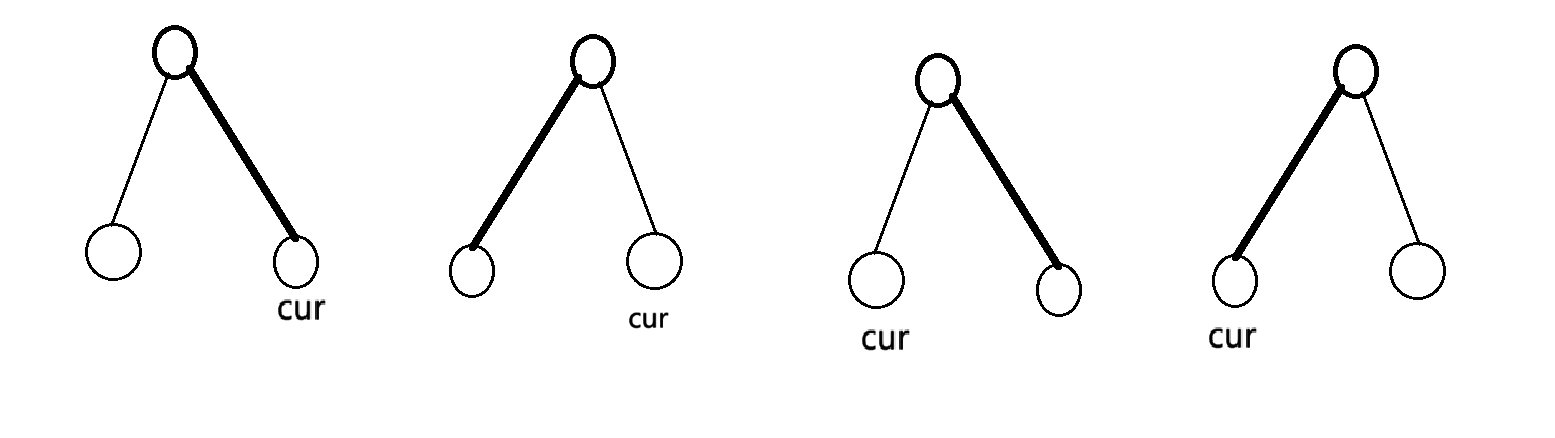
记为 1234。这时 cur 位于右侧意味着和定值合并（很唐的是我很长一段时间以为树上节点是 \(n\log n\)，，，），定值容易预处理；位于左侧意味着和未定值合并，这些未定值显然彼此等价都可以成为获胜者，预处理和即可。

2 是最傻逼的，要么不变要么替换为某定值。在树上先 dfs 一遍找出每个位置被替换的最晚位置，这是 \(O(n)\) 的。

3 其次。3 的作用是把右侧的未定值加入，无条件。

1 是（记轮数为 \(k\)）把 \(<k\) 的定值去除掉（简称扔垃圾），然后如果至少扔了一个垃圾或者存在未定值，就把左边的定值加入。

4 是扔垃圾，如果扔了垃圾或者存在未定值就加入右侧未定值，否则不管。

观察过程，我可以从最后一个有影响力的 2 开始做，忽略后面的 2；然后后面的 1，4 和未定值是否存在有很大关系，因此试图找到未定值加入的位置。这有个好处是在这之前定值不超过一个数，于是直接扫描即可。后面的找到最后一次扔垃圾位置，（存在过的）定值是否能存活到最后之跟这个位置有关系，每次在 1 操作加入定值时判断是不是会被扔垃圾即可。然后这样是 \(O(Tn\log n)\)，预期 84~100。

插入正解：这 byd 不就是到根的链的处理吗？找到第一个自己的定值被替换位置（\(O(n)\)），然后在树上从上到下统一处理就是 \(O(n)\)。不知道场上在吃什么史。但是 \(O(Tn)\) 就算写也不知道写不写得出来。

然后苦难思考，在序列上有什么方法能 \(O(1)\)。非常傻逼，没想到。于是开写 \(O(Tn\log n)\)（16:30），写写写，写到了 17:00 终于写出了第一版。发现过不去小样例。改改改，小样例的四组数据都挂了一次，，，然后调到了 17:30，通过了 1235 样例，4 样例没通过？？（如果是我们的构式联考一开始那版代码就可以通过所有的样例，，，确信）调大数组无果，瞪了一会之后发现当时写的默认扔垃圾是最后一次，但是最后的后缀是 23 操作就不会扔垃圾。改改改，在 18:00 通过了样例 4。

测极限数据发现需要 2+o(1) 秒，但是我们这是神机啊（比 CCF 快一点）？？然后卡卡卡，对卡常一点不熟，卡到了本机 1.7s，然后觉得过 92 没啥问题遂下拨，重审了前三题，然后就在系统时间 18：26 的时候突然有人大叫，然后比赛结束了？？幸好我交了程序。

CSP-S2 总结

做前三题步调慢了一些，一个原因是觉得前三题的难度相对于之前过于奇异。

第四题场上调试时间还算合理，但是未知为什么没有想到正解。可能由于我场上一直考虑快速处理序列却忽略了树的结构和很长一段时间认为树上节点是 \(n\log n\) 的。

现在突然发现那个我以为是 \(O(Tn\log^2n)\) 的暴力是 \(O(Tn\log n)\) 的！！不知道我在干什么