Recent 做题记录
奇异搞笑的写 INF 篇题解计划。联考题见另一篇博客。
2023.9
LCT 相关和水题被移除了。
CF922D 考虑交换法即可。Livshits-Kladov 定理。
CF1528C 第一棵树上是一条链;第二棵树上使用数据结构维护贪心(小的区间比大的更优;树上具有包含/无交性质)。
ARC100E/CF1208F SOS dp 模板。
P1081 开车过程可以倍增优化。于是直接 dp 即可。
P5633 wqs 二分模板。
P4948
首先注意到的是本题不弱于 \(\sum_n n^k\),所以插值大概率是逃不掉的。
然后一个神秘的结论是:
其中 \(g\) 为一 \(k\) 次多项式。这个结论是容易使用数学归纳法证明的(由于 \(k\) 次多项式在加减、移位下封闭),但是实在不清楚是怎么发现的。
\(g(i)\) 就是可以递推的,然后插值就可以了。关于 \(g(0)\),使用高阶差分就可以得出一个方程。
P5068
按照伤害值分成 \(O(n\log n)\) 段,这也是所有伤害值答案的总修改次数上限,因此是可能暴力移动答案的。快速找到需要移动的区间是容易的:挂到线段树上就可以了。
(闲话:离线的做 \(O(1)\) 询问哪些被修改是可以的(当 \(q>O(n)\)):挂到 ST 表上)
P1248
比较不知所云的 Johnson 算法。先按 \(sgn(a_i-b_i)\) 排序,然后再按 \(\min(a_i,b_j)<\min(a_j,b_i)\) 排序。
关键是据说有邻项交换需要满足“严格弱序”的说法,但是到现在我也不是很清楚,,,
P5488 生成函数的一个小应用。还没有知道更好的理解方式。
P7962
主要的关键性质是交换后的差分数组成单谷.
当时觉得这个结论十分奇异,但现在看来完全是能推的。dp 就是容易的了。
P1251(非网络流)
又是一个单谷题,只是使用的是贪心。
我需要确定买餐巾的个数。(甚至是凸的,根据费用流模型?)单谷性是容易理解的。
贪心的过程大概是认为餐巾都是预先买好的(感觉和最近连考题的 cf1949h 的有点像???),然后优先用新的,否则先尽量从前面透支慢洗再用快洗。
P8162 肯定需要所有人在一起办事,然后枚举一下协作者个数之后随便做就可以了。
P5907 换成线性插值就可以了。。。
P2901 可以使用 A* 通过的 k 短路。
A* 的大概思路是按照当前点代价加上到终点的估价,其中估价小于实际代价。
这里我估价为到终点最短路就可以了。感觉可持久化可并堆那玩意太复杂并且本来 k 短路就没见过。。
P4451 分式转(二阶)递推式的小练习。
P2534 IDA*。
P2519 经典读题错误。这个每个人实际上说的就是哪一段区间(极长)是得分相同的。选尽量多的区间使得相互不矛盾是 BIT 优化 dp。
P3147 直接倍增 dp 即可。但是另一种很蠢的想法是考虑权值和为 \(2^k\) 的区间然后分半。
P3287
一个显然的观察是一定是后缀加一。然后直接 BIT 优化 dp 即可。
P4381 奇史无比的季桓叔题目。这个题只需要求直径。要么跨越一段环,要么就是环的子树的直径。这些都是好做的。
P3647 直接考虑一个点是有没有上传蓝线的。比较麻烦的一点是我需要换根。但是换根也不是不能做。
ABC252H 因为 \(n,c\le 70\),所以实际上状态不会特别多。我虽然不会处理多 trie 问题,但是两个合并还是会的。所以直接 meet in middle 即可。
P4767 及其加强版
非常经典的 \(O(n\log^2 n)\) 做序列划分问题。证明一下四边形不等式然后 wqs 二分就可以了。这道题四边形不等式证明是容易的。
CF1423L 一眼看上去是异或高斯消元什么的,但是我要最大解。第二眼 meet in middle。
P4516 没什么意思而且很麻烦的树形 dp。
P2767 广义二项级数的组合意义(之一)。
P5395 经典的式子。一个导出方法是把下降幂式子
二项式反演掉。
P5824
比较有意思的是计算拆分数(给定部分),别的就是小学数学。这是付公主的背包 trick 的第一次看见(\(\ln\) 之后展开为 \(O(n\log n)\) 项相加再 \(\exp\) 回去)。
P5408
倍增 NTT。我需要从 \(f(x)\) 的系数求 \(f(x+n)\) 的系数,这个做一次乘法即可。
P6620
在当年省选定位不明的题目(D1T2)。
一个想法是把 \(x^k\binom nk\) 凑起来,有一个想法是 \(n\) 太大了用斯特林数搞一下,就结束了。
P5409 EGF 即可。
P5396:和 P5408 像啊,很像啊(?)
P2791
和 P6620 差不多的暴力推狮子题目。一个感觉是这类题目就和当时初二疯狂练的建系暴力差不多……现在觉得没什么意思。
P5590 那么到任意路径每个点也是等长的。差分约束结束。
P4630 圆方树一下,然后 \(c\) 必须在 \(s-f\) 路径上。
CF487E 这一类考虑全部路径的题目都可以想想圆方树。这差不多就是圆方树上两方的最短距离,,,
CF1361E
NOI 树形图!首先一个点是好点的充要条件是 dfs 树只有横叉边和返祖边。这道题我可以随机到一个好点。(判断好点并不是很容易。。)然后一个点只需要看子树内(不唯一就寄)连向的点的好坏就可以了。
P5900 MSET 的最初应用。这里的方程就是 \(F=MSET(F)\)(如果有根)。这里在 \(\bmod x^n\) 意义下作的牛迭时候和付公主的背包差不多了。
P6667 做法比较多,比较通行的方法是下降幂和斯特林数那一坨。
但是这个学的时候的是 Binomial Sum。这里可以参见我的 Poly 课件了,虽然我有点小忘记了(还是理解不深刻)
P6597 无标号无根树计数带上儿子个数限制 \(k\) 的做法。
终于不需要 MSET 这个麻烦玩意了。这里的想法是使用 Burnside 引理计数:枚举所有 \(x\in S_k\),求出在 \(x\) 作用下不变的子树构造。比方说我要求全部相同就是 \(F(x^3)\)。
P2801 一个常见的复杂度 \(O(q\sqrt{n\log n})\) 不要变成 \(O(q\sqrt n\log n)\) 的关键是散块修改使用归并。
P4500 异常困难且复杂,并且目前我还对这道题没有什么非常优秀的想法或者理解,所以暂且搁置。
P8879
如果所有 \(b_i\) 都和 \(\frac{a_i}{2}\) 相等,那是最好的。现在 \(b\) 具有不降的要求,我考虑把后缀 \([L,n]\) 加上 \(dx\),答案不应增加;因此:
然而,在 \(L=1\) 或者 \(b_L>b_{L-1}\) 的位置减去 \(dx\) 再结合上面的式子将得到:
因此,任何一个连续相等段全都取 \(\frac{a}{2}\) 的平均值。根据不等式还得到:第一个 \(b\) 一定 \(\le \frac a2\)。
在调整过程中,容易证明我一定不会拆开某一段。因此,我只需考虑一个下降的数对前面数的改变;
方法是不断向前取平均值直到满足递增性质。
2023.10
类欧题被去掉了。
CF582D 整个数位地皮就是一坨史,这个题就是史中的袅。
CF961G 略显繁琐的推狮子题。
CF765F
经典老提。
支配对做法:现需要拆为 \(a_i>a_j,a_i-a_j,i>j\) 部分和对称的。这一部分找点是容易的,而若已找到 \(a_i-a_j\),则需要找 \(a_i-a_k\) 当 \(a_k<\frac{a_i+a_j}{2}\),否则 \(k\) 将在 \(j\) 处贡献。因此差每次至少减半,需要找的只有 \(\log\) 段。
分块做法:
好处是可以在线,并且只需要依赖排序后相邻的才有贡献。
分块,块内暴力处理,块间双指针然后前缀一下。散块到整块双指针处理一下每个点到每个块的答案,然后前缀一下,就可以处理散块贡献,
P4548 有一个停时定理的解释,但是一般的做法是 PGF。
设 \(f_i\) 为正好在 \(i\) 时刻停止的概率,\(g_i\) 为 \(i\) 时刻尚未停止的概率。
需要得到两个式子:首先显然 \(f_i=g_{i-1}-g_{i}\)。
一个想法是在后面加一个 \(S\) 串(这里设 \(n\) 为字符串长度,\(m=|\Sigma|\)),这样的概率是 \(m^{-n}\)。现在我枚举已有的 border 长度,就有:
转写为生成函数即可。
P2491
首先考虑 \(s=+\infty\);这个时候容易证明,答案是直径。
否则类似地,答案是直径上的一段。双指针什么的一下就可以了。
CF1867F
观察:如果一个子树不和 \(G\) 任意子树同构,其祖先均不和任意 \(G\) 子树同构,子孙均和某 \(G\) 子树同构。
因此,只需找到最小的这样子树就可以了(然后向上延申)。这是容易的。
P4345
比较少见的 Lucas 辅助推狮子。考虑到 mod 很小,使用 Lucas 定理把指标降下去。
P4707 经典(?)的 min-max 容斥,然后用 dp 计算答案的题目。最后一次/多次出现的题目都可以考虑 min-max 容斥。
CF960G 比较香的一点是我从大到小插入不会改变之前的值的性质,放首/尾各为前/后缀最大值。因此写出生成函数式子 \(xy(x+y)(x+y+1)\dots (x+y+n-1)\),用斯特林数展开上升幂。
P3214 构式题面,但是一个观察是第三个条件实际上是消去一个集合;第二个条件去重容斥掉即可。
SP22343 和 min-max 有关的计算可以考虑最值分治。但是好像不行。我还是直接分治。枚举一下 min/max 在哪边,搞搞单调栈,,看上去是十分可做的(只是很麻烦)
P3343
考虑积分求概率密度什么的可以搞出一个有点奇怪的做法(?)
斯特林反演可以处理连通块的容斥问题:钦定有 \(k\) 个连通块和恰好有 \(k\) 个连通块之间是斯特林繁衍的关系。这样,我只需考虑钦定有 \(k\) 个连通块了。(虽然这个 dp 并不是很容易,。,)
P4211 先差分。扫描 \(r\),需要对所有 \(z\) 累加贡献。这就相当于对 \(1\to z\) 的链每个点子树 \(+1\)。搞成链加一查询到根路径和即可。
P3176 由于矩阵乘法有分配律,直接把矩阵作为 dp 值。
ABC246H 认为一个子序列生成方式为从后往前做尽量取后面的值,这样我就可以 dp 了。修改 DDP 即可。
P3571 神秘!!结论。为策略为在前 dep 层花 dep 次覆盖(dep 为某深度),下面的每次都能顶满 \(k\)。然后斜率优化。
P4091 有限微积分的小应用。需要先把斯特林数拆开。
P3349 利用子集反演去掉 dp 的排列限制。
P5591 \(i\bmod k\) 和 \(\lfloor \frac ik\rfloor\) 都可以使用单位根反演化简。
P3188 现在看上去没什么神秘的。按照 \(a\times 2^b\) 把 \(b\) 从大往小扫描,并枚举一下体积。如果 \(V\ge 1000\) 就直接视为 INF。还需枚举下传多少个到 \(b-1\)。
2023.11
string 题被去掉了。
为什么?
(note:震撼世界的十天)
CF1806F2
考虑 \(k=1\)。假设序列不重:不难证明总是选择最小数和某数合并。因此,最终答案缩出来的是一个包含 \(a_1\) 的 \(k+1\) 元集合和别的散的。求答案枚举去掉的重数个数即可。假设现在需要 \(t\) 元集合(去掉删重数)。
一个神秘的想法是:把方案调整:选取最小未选取的,删去最大选取的。计算得到:这样变得更优,当前 \(t-1\) 小全选取。
gcd 拥有的性质:只有 \(\log\) 次变化。这样就可以在 \(O(n\log^2 V)\) 解决问题。
P4151 dfs 树跑出一条路径之后,新路径的权值相当于异或上若干个环:而这些环构成的线性基相当于返祖边和树链构成的,由于异或。这个结论在其他题目也有一些应用。
P8867 缩边双,边双内部的边没有任何影响。之后限制就是每两个选了点的边双之间的桥必须全选,这个直接树形 dp 即可。
P5320 高级做法不会,一般做法是推狮子然后在模意义二次域下做运算。
CF1559E 首先对 gcd 容斥算下系数,这不是我们莫反吗。然后 \(n\) 非常小直接做就可以了。
P6864 括号串相关神秘。操作一会增加一个后缀匹配串并且答案会增加后缀匹配串个数。操作二使答案 \(+1\),后缀匹配串变为 \(1\)。矩阵维护,结束!
P7706 闹钟题。注意到 \(\min\) 是假的,合并的时候枚举一下 \(j\) 取哪边即可。
P6617 利用一个偏序性质,如果 \(a_i=a_j\),且 \(i,j\) 的前驱一样,\(j\) 就废了。这样,一次修改只需要修改 \(O(1)\) 个值。
P9061 去维护那个阶梯状物上的点。阶梯有个好处:关于 \(x,y\) 均单调且相对顺序一致,这告诉我们可以使用平衡树维护阶梯上的点。每个点进入阶梯是二维数点。每次询问操作熔池得到需要计算 \(x\le X,y\le Y\) 的已覆盖点和若干次二维数点;修改需要拿一段数来打覆盖 tag,这是平衡树可以做到的。
P7739 看上去就只是直接使用矩阵维护
ARC110F 神秘连考题。观察到(怎么观察到??)一次性给一个位置操作 \(n\) 次会让他变 \(0\)。于是从后往前操作每个 \(n\) 次就结束了。
CF1746F 经典的哈希。哈希之后求个和,看看是不是 \(k\) 的倍数即可。
P7111 根号分治相关的多项式。
P5828 两个做法。
考虑容斥割边数量。设熔池出来被钦定的边双连通块大小为 \(a_i\),根据某 Clue 结论,方案书为 \(n^{m-2}\prod a_i\),加上熔池系数变形为 \(-\frac 1{n^2}\prod (-na_i)\)。直接做。
第二个想法考虑有根。设无向连通图为 \(D\),边双是 \(B\),枚举根的边双连通块大小,得到:
需要拉饭!还只能求一项。
P4755 最值分治。
2023.12
去掉 SAM 和 PAM、竞赛图弦图这俩图逼。
P4689 换根是傻逼!!换完之后还是直接莫队即可。
P7446 分块。首先尝试维护一个点跳出块的第一个点。一个区间作为整块被操作在 \(\sqrt n\) 次之后就会全部指向 \(a_x\);所以我每次修改暴力操作是可行的。
P4690 直接可多隶属搞 pre 修改然后变成了二维数点问题。
P4173 多项式处理匹配的时候的经典是 \((a_i-b_i)^2\)。如果需要通配符就是 \(a_ib_i(a_i-b_i)^2\)。
P7561 这里比较方便的是让两维独立一点。曼哈顿距离转切比雪夫距离之后二分+数据结构维护即可。
P7880 支配性质是 \(l\le l'\le r'\le r\) 的话 \([l,r]\) 是无效的。最后如果我得到了若干点对我直接扫描线数颜色就可以了。处理点对启发式合并,合并的时候一个值加入只会造成 \(2\) 对贡献。
P5314 书剖之后平衡树维护轻儿子平衡树。
CF1017G 鼎汉。注意到染黑和顺序(不考虑染白)是无关的,进一步发现设权值维护一下后缀和什么的就可以了。子树染白是容易的。
P3772 鼎汉。矩阵乘法。
CF1416F 画出季桓叔。容易发现环是偶环,因此可以拆成若干二元环。二元环可以用匹配刻画。考虑什么样的边必须要在环上:没有周边小于他的。使用上下界可行流跑出结果之后容易证明这样的限制是充要的。
P2839 比较套路的一点是中位数相关设 \(<\) 为 \(-1\),\(>\) 为 \(1\)。
CF536E 唐逼题,扫描线+书剖
ARC132E 最终形态是 <<<<=>>>>>>。然后随便统计一下。
CF1019E 把 \((\sum a,\sum b)\) 组织成一个上凸壳,闵可夫斯基和合并即可。
P6108 先拆式子。比较有优势的是把 \(\frac{1}{k+1}\) 通过定积分搞成 \(x^k\) 的形式,和二项式系数配合。
CF1603F q-binomial 和线性空间相关的计数。现在不太会,但不是很难。
P9058 淀粉质的时候支配一下。
P4220 第一棵树淀粉质哈夫曼树合并(不会便分支,,)第二棵树建虚树,在虚树上合并一下第三棵树的最短路。
UVA12370 香浓游戏和拟阵交题。不会的
P6976 搞个重心边 分治,以为很麻烦但是直接处理端点到每个点最短路然后递归。
P6237 可以直接极角 LCT,但是注意到是多边形只在端点相交,即不在端点的话相对顺序不变,set 维护一下即可。
P4827 拆斯特林数出组合数之后经常可以得到一个可以 dp 的形式(因为组合数)。还有一道这样的题。
CF632F 显然是图。仔细思考发现这个条件是说,\(<a_{i,j}\) 的边只保留,\(i,j\) 不连通。MST 即可。
P3642 板子
AGC035D 一个数的贡献系数是 \(O(2^n)\) 的。因此设 \(f(i,j,cl,cr)\) 是 \(i,j\) 被计算 \(cl,cr\) 次的区间 \([i,j]\) 删到只剩两边的代价。理性(题解)分析状态数是对的。
CF527E 定向问题等价于存在欧拉回路,也就是所有点度数为偶数。直接加边跑即可。
CF547D 直接连 \((x_i,i),(i,y_i)\) 然后上下界网络流。
CF1603D 莫反推狮子然后发现具有四边形不等式性质!决策单调性分治。
ABC226H dp \([1,i]\) 放了多少,\((i,i+1]\) 放了多少,运用经典结论转移。
P4747 好像是西河树板子。
2024.1
CF1089I 西河树计数。好像直接 dp 就可以了
P5748 贝尔数,符号化直接做
CF1610H 一个事情是非祖先-后代的链选 \(1\) 就可以全杀掉,所以先考虑“直链”。这个很容易,选祖先到后代第一个点就可以了,从深到浅做。这样个好处就是这也是尽量满足“曲链”的选择,因此有不满足的给他来个 \(1\) 就可以了。有 dp 做法。
CF1528F 另一个推狮子题目。
CF1477F 神迷题!首先知道那个分布之后巨大推狮子。详见https://www.cnblogs.com/british-union/p/17938839/Imwin。
P6624 看到 gcd 用莫反容斥掉,然后就是矩阵书板子了。
CF1070L 关键结论:答案 \(\le 2\)。
证明:这里的方程是 \(\oplus x_j=(x_i\oplus 1)/0\),取决于 \(2\nmid \deg_i\) 或否。
如果说无解,即有方程异或出来是 \(1=0\)。这样的方程是说,有奇数个中心 deg 为奇数的方程,每个点都被覆盖偶数次。这就是说把这些点的导出子图拿出来,所有点的度数和为奇数,但这是不可能的。
P4000 关于斐波那契的循环节。有两种做法:
第一种,\(\bmod p\) 周期 \(\le 6p\),则找出来矩阵 BSGS 即可,复杂度 \(\tilde O(\sqrt p)\)。
第二种神秘结论,对 \(p\) 质因数分解然后求最小公倍数。需求模 \(p^k\) 周期,神秘结论是 \(p^{k-1}\) 乘上 \(p\) 周期是 \(p^k\) 周期。还有结论是 \(p-1\) 是 \(p\equiv 1,4\pmod 5\) 的周期,\(2p+2\) 是\(p\equiv 2,3\pmod 5\) 的周期,有点阴间,但是很好写。
CF1034E 神秘的构造。直接子集卷积不太行,想法是考虑 \(a_i\mapsto a_ix^{|i|}\),由于值域很小,取 \(x\) 为大数然后直接卷积即可。但是事实上只需要 \(x=4\)!原因是如果 \(i\cap j\neq 0\),那么 \(|i|+|j|\) 就会贡献飞,\(|i|+|j|>|i\cup j|\)。
CF839E 不能负数,否则就拉格朗日乘数法了。注意到找到最大团然后平均一下最好。最大团是可以很快的。
CF1446D2 关键结论!原序列众数一定出现,否则可以扩张区间直到原序列众数成为众数。然后根号分支一下什么的。
CF963E 主元法的板子。从左推到右即可。
ARC156F 不挑战 怕战胜 困困困 难难难
P1742 最小圆覆盖!做法是随机打乱后每次加入一个点,如果不在⚪里头就重置圆覆盖,扫描 j 从 \(1\) 到 \(i\),如果不在就把 \((i,j)\) 当成新圆的直径,然后扫描 k 从 \(1\) 到 \(j\),如果不在圆上就把 \(i,j,k\) 的外接圆置为圆覆盖。
这正确性是有的。试证明:
引理 :\(P\not\in \triangle ijk\iff \exists \{a,b\}\subset\{i,j,k\},i,j,k,P\in \triangle abP\)。
如果 \(k'\) 使得当前 \(i,j,k\) 不满足 \(k'\in Circ(i,j,k)\),那么有:
那么有 \(k'\in \triangle ijk\),矛盾!
然后复杂度大概是这样:
每个点更新最小圆覆盖的概率是 \(O(\frac 1i)\);第二层循环的进入第三层的概率也是 \(O(\frac 1j)\),所以第二层是 \(O(i)\) 的;因此一次是均摊期望 \(O(1)\) 的(不太会说话,,,)。
和这个应用同一个技巧的是平面最近点对。设目前答案为 \(d\),平面按 \(d\) 分块,每次加入点扫描附近 \(9\) 个块(注意到一个块不能有三个数),有更新答案就重构平面分块。一次更新答案的概率是 \(O(\frac 1i)\),重构的代价是 \(O(i)\),是期望线性!!
都需要 random_shuffle。
P4586 在这里的做法是把点按照交点连线劈开分成两部分,相当于对于某个斜率分两部分点然后求最小圆覆盖。枚举斜率即可。
CF578F 我想的是光线在那个半格的连通块的两端走;但是这样不是很易于搞。
另一种想法是考虑格子交点的点阵的连边。这样的有个神秘的事情:合法当且仅当(黑白染色后)黑点/白点连出生成树,显然这两种情况是不交的。这成立,因为考虑两种边界匹配情况(对应白/黑):那个连通块的“壁”必须连通,即边界黑点连通;而每个半格都必须被遍历,即炼出了生成树。
之后矩阵树定理即可。
CF838D 一个神秘模型。把他搞成一个环,再首尾之间加个点。然后不生气当且仅当新位置没人做。然后考虑所有位置是等价的(认为可以选取新位置)!然后概率就算出来了。
ARC141C 怎么求 P,Q?在折线图上 x 轴以上的部分直接推过去,否则在 x 轴以下的部分先取一个后面的 ( 再来个左边的 ) 直到取完这部分。
因此判断 \(P_{2i-1}\) 和 \(P_{2i}\) 的关系;如果 \(>\) 就可以确定这是拿的左括号/右括号。然后 \(Q\) 补上了其余的部分。
AGC056D 巨大苦难题!主要内容在[题解]里,主要观察是不能存在 \((x,w),(y,z)\) 的策略组,其中 \(x\le y\le z\le w\)。
AGC058F 这里主要的神秘的事情是系数 \(\frac 1n\),如果是 \(\frac{1}{n-1}\),那就是对删边的概率说法(最后答案好像是 \(1\),,)。但是 \(n\)。这里的想法是对边加点,再给每个边点下面挂一个大小为 \(-1\) 的点,或者说挂 \(998244352\) 个点。现在就是删点使得最后剩下的是原来的点的概率。
建出拓扑序的图(贺的)。
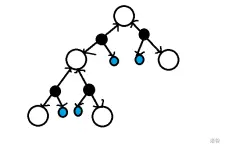
对指向下面的边容斥为不存在边/指向上面。然后树形 dp,记一下子树大小(经典结论之拓扑序概率)。
P5472 好像是有点神秘的题,等一等
P5280 感觉很困难??把点分为几类,这几类的点在修改时行为是一样的(图贺的):

设每个点在 \(f_u\) 个树上有 tag,\(g_u\) 个点到根的路径上有 tag。然后我们发现信息是可以转移的。(废话)
P6073 没什么实际用途的欧拉数巨大题目。
P2179 拉格朗日乘数法的板子
CF490F 树上最长上升子序列。一种做法是记 \(f/g_x\) 是 \(x\) 的走下去的 LDS/LIS,然后线段树合并。统计贡献是什么 \(f_x+g_y+[a_x<a_u<a_y]\)。带 [] 的部分直接做,不带的话在左右合并的时候在分界统计一下即可。启发式合并也可以。
P9870 首先转化题意(这个也是我做的)求 \(A_{i,j}=[X_i<Y_j]\) 的 \((1,1)-(n,m)\) 连通性。接下来是特殊性质,即走到边框即可走到 \((n,m)\),否则无解。然后这个图具有神秘的支配性。考察行 xmax 和 ymin,xmax 可能缩小边框范围,当 \(ymax_2\le xmax\le ymax\) 才不行。同样 ymin 也可能缩小边框范围。这样一直找 min/max(当然是前缀的),缩小不到 \((1,1)\) 或者发现无解才不行。
离开特殊性质是类似的。从 \((1,1)\) 和 \((n,m)\) 分别做即可。现在看上去没那么神秘?
P7438 把多项式拆成牛顿级数,现在只需求 \(\binom {cyc(\pi)}{i}\)。转写为二元 GF,这是 D-finite 于是递推即可。
P3779 中心极限定理,用数值积分来计算正态分布的那个玩意。小数据 FFT。
P8883 一个数不被 \(d^2\) 整除的概率是 \(\prod_p (1-\frac{1}{p^2})\approx \zeta(2)=\frac{\pi^2}{6}\)。
SP8073 圆的面积并。把一个 x 覆盖的 y 的范围当成函数直接数值积分!!注意连通块分开。
P5540 假设找出来一个 \((\sum a,\sum b)\) 点在二维平面上。我要找到一个凸包,考虑用直线去切他,直到找到所有的凸包点。这就是所谓的 quickhull 算法。
AGC055D 神秘结论提。设 B-A 的前缀最大值是 \(x_1\),同样 C-B,A-C。那么合法的充要条件是
\(x_1+x_2+x_3\le n\)。
必要性不难发现。构造是取第 \(i,i+x_1,i+x_1+x_2\) 个 A/B/C。神秘!
P1573 四柱汉诺塔,当时看得懂觉得很妙,但是现在看不懂我在写啥
P3236 这还是 quickhull 系列提,但是变成了最大权完美匹配。当时联考还有个线性基的。
2024.2
P5492 似乎直接状压 dp 即可。
P5644 这种没什么好模型的玩意尝试容斥。设 \(f(S)\) 为至少存活 \(S\) 的概率,即求 \(\sum (-1)^{|S|}f(S)\)。求 \(f(S)\) 的方法是随便杀杀杀杀直到杀到 \(1\)。这个概率很好算,直接列式子。然后后面的部分是简单的。
P8340 首先是神秘数关于集合表出的结论。这告诉我们:设 \(a_{i+1}\) 为可以表出 \([i]\),且和为 \(i\) 的集合个数。知道 $\langle a\rangle $ 之后答案容易求得。
我们容易把 \(z^{k}(1+z^{k+1})(1+z^{k+2})\dots\) 写成 q-级数的形式,其中 \(q=z^k\)。
照样可以写出 \(F(q)=F(qz)(q+1)\)。于是
那么:
若设 \(A(z)=\sum a_iz^i\),那么:
这样就可以从高次到低次做 \(j\) 拉。
P3321 原根转化为加法之后是循环卷积直接做。
P4705 求幂和有几种方案:牛顿公式(讲道理我忘了),或者用 GF 化为 \(\sum \frac{1}{1-a_ix}\),然后直接加法(常熟大)或者求导分治 NTT。
CF1392H 有不少做法,一个都不会
AT_xmascon19_e 利用勒让德定理,化为求解 \(\pi(\lfloor \frac ni\rfloor)\)。这个采用 min-25 筛类似的 dp,即设 \(f_{i,j}\) 为 \(n/i\) 内最小质因子 \(\ge p_j\) 的个数。则有 \(f_{i,j}-f_{i,j+1}=f_{i/p_i,j}-j\),复杂度为 \(O(\pi(\sqrt n)\sqrt n)\)。
AT_xmascon19_d 这直接是机型函数,,,可以 Min-25,也可以杜教筛。考虑 \((-1)^f * 1=[\mu(n)=0]\)。
P3249 首先平面图转对偶图。这个时候提取出边界的边,如果在内部的面是儿子就加上子树和,否则减去儿子的子树和。
平面图转对偶图(划分区域,也是 SCOI2024 D1T2 比较麻烦的一个步骤!)边拆成两条有向边然后极角排序从小到大做,对于 \((s,t)\) 其多边形的下一条边就是 \((t,s)\) 在 \(t\) 那里的上一条边。
P9477 信息熵那一块不太懂,希望以后严密地学一下。另一种看法是“概率权值”。询问一次 \(y\) 如果发现 \(>x\) 就把 \(1\sim y-1\) 的全都乘上权值 \(1-p\),\(y\) 变成 \(0\),\(y+1\) 乘上 \(p\)。
每次为了得到最大的信息(使权值更不平衡),找到全局概率权值之和靠近一半的位置询问。
CF600F 神秘技巧之二分图染色。可以做限制用一个网络流难以表达的题(还多的限制),比方说 [SNOI2024] 拉丁方。
二分图边色数等于最大度数(神秘结论 \(2\) 之一般图边色数 \(\le\) 最大度数 \(+1\))。构造方案:对于每条边 \((u,v)\),若其未被染色,找出 \(u,v\) 的最小未填颜色 \(l_u,l_v\)。若 \(l_u<l_v\),那么找出 \(v\) 连出去的 \(l_v\) 色到 \(x\),再找 \(x\) 连出去的 \(l_u\)(如果有)……这样找到不能进行。这样的增广路是不包含 \(u\) 的,因此把每个边 \(l_u,l_v\) 反转颜色即可。然后 \((u,v)\) 设为 \(l_u\)。
2024.3
P5311 cdqz的竞赛教练林老师/qd 点分树上跳父亲找出最浅的结点,然后就直接在这个点子树里询问了(跟 \(x\) 没关系),就是二维数颜色,这个扫描 \(x\),维护颜色在 \(y\) 最小的出现位置然后数即可(?)。
P4566 组织成树,然后我只关心儿子个数。现在我们设 \(f_k\) 是具有 \(k+1\) 个儿子的节点的方案数,其生成函数是 \(F\)。
设 \(G\) 是全排列的生成函数,我们令 \(F\) 复合上 \(G\),发生了什么?这个意思是 \(k\) 个儿子全都变成了连续段,最后一个单点儿子未计数。此时,显然统计上最后一个儿子得到了全排列。所以 \(xF\circ G+x=G\)。代入 \(z=H=G^{<-1>}\)。
这个不收敛的形式不用思考拉反了,考虑微分方程来描述 \(H\) 和自己的关系。注意到 \(G\) 是微分有限的,因此 \(H\) 是微分代数的,具体来说(当然也可以直接复合逆算法!):
别的人写的都是构式,还是 251sec 是牛逼。
全在线卷积怎么做??如果需求 \(0\sim n\),设 \(m=n/2\),先求 \(0\sim m\),然后两个 \(i,j\) 不同时 \(> m\),所以是两个半在线卷积和一次乘法,直接做复杂度为 \(O(n\log^2n)\)。
P3920 静态是点分树问题,动态考虑重构点分树。如果发现一个节点的某个儿子太重了就重构,复杂度不知道。
AGC019F 转折线。
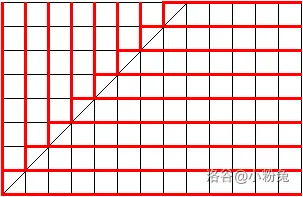
那就是和红色的橡胶长度。把在斜线上方的翻着下来,损失了斜线位置向左的。斜线位置向左的需要统计。直接做即可。
P5286 一个做法是:等腰三角形只有 \(O(n^{2+o(1)})\) 个,差不多是 2.14。然后暴力枚举!!否则是神秘的枚举。
CF1227G
素质极高题面:
神秘构造,不是很懂,但是可以通过递归构造,每次干掉 min 来处理。
P6295 DAG 计数的板子。枚举钦定的 0 入度点,容斥这一点即可。
P9394 双极定向那一坨,现在不太会。
CF702F 扫描物品,设价值为 \(c\)。询问分为 \(x<c,c\le x<2c,x\ge 2c\)。第三部分不改变相对顺序,第二部分暴力即可。
CF1548E 找代表元。容易想到的是一个连通块的代表元是 x,y 两维的最小值位置,这应该至少形成一个十字形。因此一个位置被统计当两边最小的都走不到。直接计数即可。
P7126 苦难的代表元题目。bfs 序考虑,则选取 bfs 序最小的代表元。这样的代表元只需满足不向更小的 bfs 序连边,证明略。然后容易。
ABC242H 先 min-max 容斥,然后似乎直接 dp 即可。
P8512 忘了颜色段均摊?直接 ODT 记录一下每个颜色段在什么时候出现即可。
P10218 按位贪心。如果 \(x\) 这一位取 \(1\),那么要求 1 子树全都是加法;如果满足进入 0 子树,只需减 \(m\)。否则不可行,存在异或使得这一位是 \(0\)。而此时 0 子树答案全都在这一位是 1,无需考虑,可以全都分配异或,进入 1 子树计算。
如果 x 取 0,则要求 0 全都是加法(也不一定满足)。如果可以满足条件进入 1 子树;否则此时 1 不影响答案,全都分配异或进入 0 子树计算。
在已经由于某些问题使得当前位不可能为 \(1\) 的情况下差不多处理。
P4542 首先设 \(d_{i,j}\) 为 \(i\to j\) 不经过 \(>\max(i,j)\) 的点的方案数。我在 \(d\) 的完全图上做最小权最多 \(k\) 的覆盖就得到了答案,这是不难发现的。
网络流。每个点拆成左部右部点,边连左部-右部,代表合并两个点(以在一个路径上),每个点向左向右连 \(1\),除了起点是 \(K\)。正确性是不难发现的。
CF1010F 哼哼啊啊啊题目(似乎在别处有出现)。只需求出根为 \(1\) 连通块大小为 \(j\) 的方案数。携程多项式就是 \(F_u=xF_LF_R+1\)。述链剖分,在重链上考虑。重链发现只需分治 FFT 解决。
P4249 首先是 \(\sum \binom {out_i}{2}\) 的最小值,然后这个差分是递增的(不知道是凸还是凹,,)。然后每个不确定局面建一个点,连向 \(a,b\) 代表这两个得有一个加一。然后最后每个人连向终点把 out 拆成一个一个一个即可。
CF1515I 赞美 1515 场(?)T-shirts 更强的 \(/2\) 题目。设 \(c\in [2^x,2^{x+1})\),则设这个范围内的是重物品,更小的轻物品,更大的不管。对于每个 \(x\) 维护一下要取全部、至少一个重物品、所有轻物品的代价,挂在线段树上,每次除非可以取一个重物品就不会往两侧递归,而这会减半,所以复杂度是 \(O(n\log^2 n)\)。
P8367 略去一大堆垃圾,重点在于处理此式
关于 \(i\) 的变化(\(k\) 是容易的)
没有尝试使用代数(AGC019F 的经历,,,),这个使用组合意义的重点在于求和上界转为 \(i\)。这是不难的:
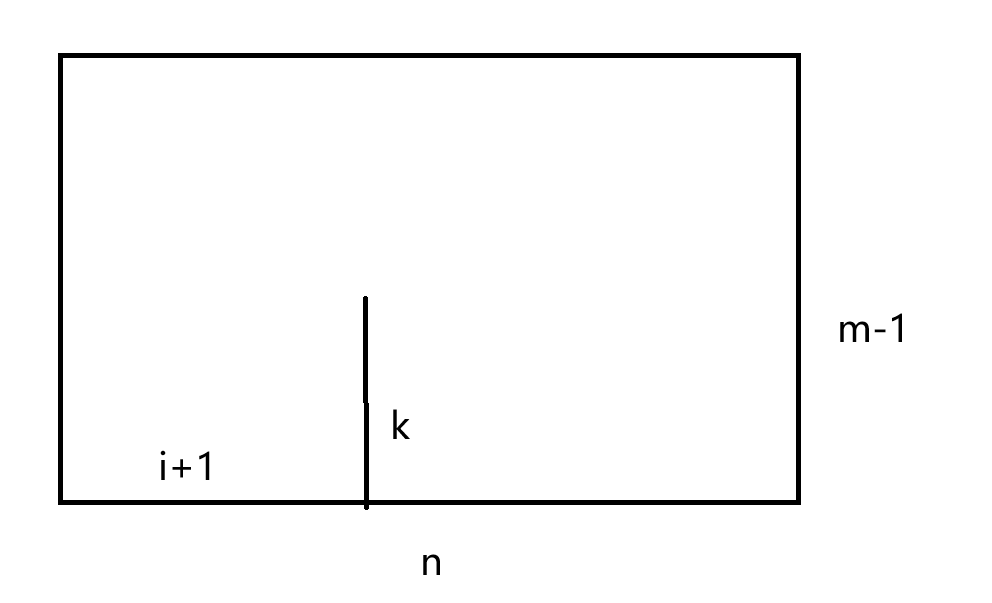
即左下到右上的格路,经过那条线段的方案数。这个很容易,把这玩意反转一下即可,就是说路径每个 R/U 取反:
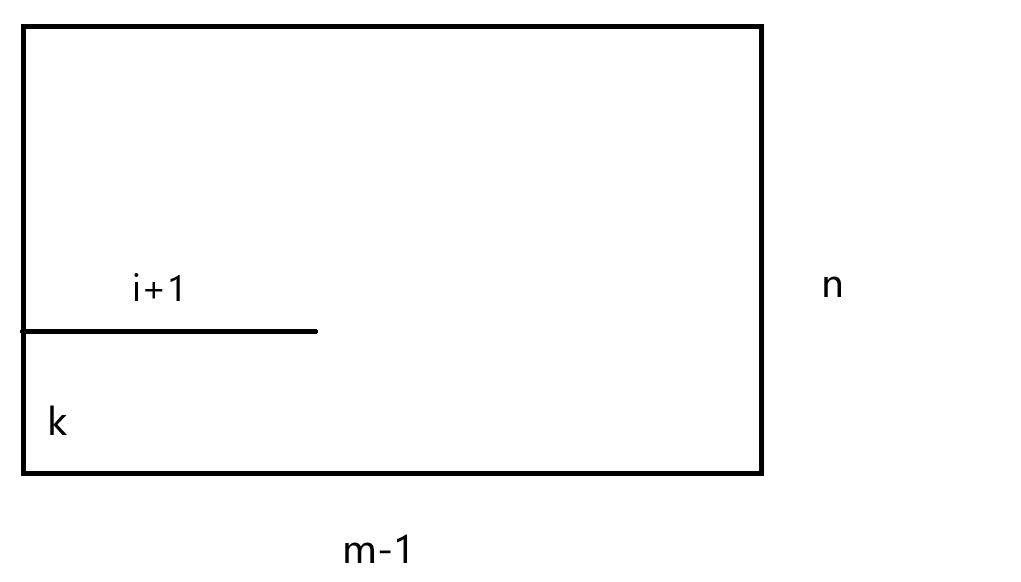
CF1682F ?
CF1383F 最大流等于最小割。这些边枚举一下,暴力跑过不了,但是只要加边情况,残量网络跑。
P6672 搞一下发现是减去一之后前缀和 \(\ge 0\)。
Raney 引理:一个和为 \(1\) 的数列恰有一个循环位移使得前缀和全都是正数。
因此手动加个一即可,,,
P10220 和 D1T2 莫名对偶,,,设 \(f_{u,i}\) 为 \(u\) 点使得第一个 \(\ge i\) 的最少钱。这个随便转移就可以了。然后 dfs 也是容易的。(话这么说但是写的时候调了巨久,,,)
P3347 神秘。考虑增大单位流量限制,即不流瞬时流量 \(>\lambda\) 的流量的最大流 \(f(\lambda)\)。看上去这应该是凸的若干段一次函数。拿出来积分即可(?)
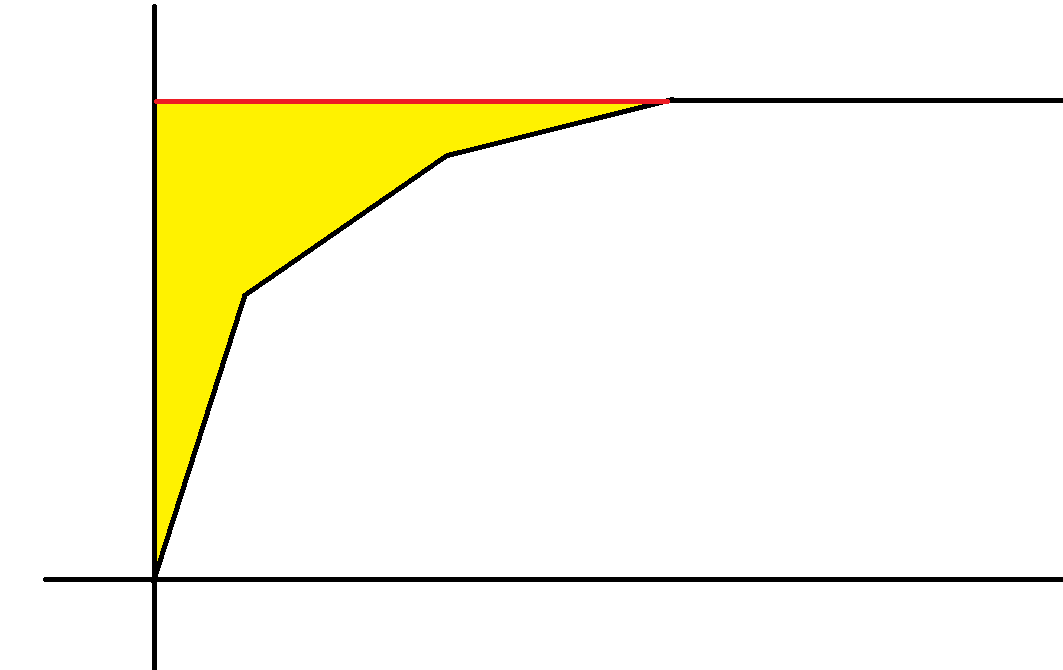
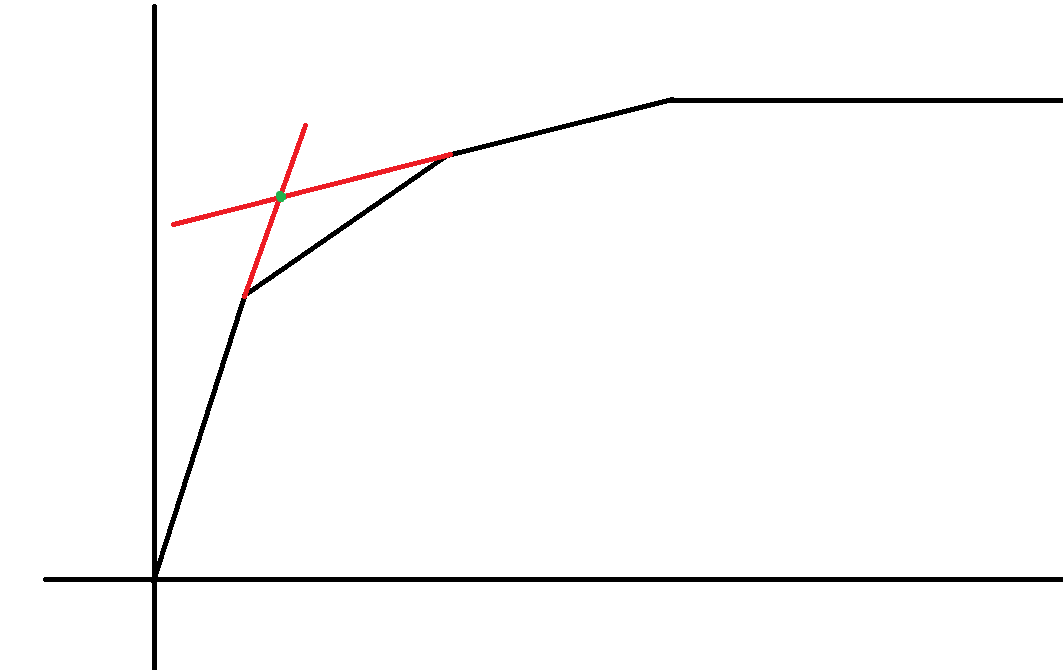
一次函数用这样的分支方法求出:
P4198 单侧递归线段树模板。
P10221 疑似有点唐??首先是拓扑序计数,然后计数一个点集划分为 i 个无连边点的方案数(用来 DAG 容斥),然后 DAG 容斥即可。事实就是这样??
P10222 序数题目,看起来就是得出若干结论然后 DS 优化,而航航场切了。
CF1530F 似乎直接熔池即可?注意一行转移的话直接略去全 1 就行
CF1539E 神秘题目。一个 \(x\) 连续段需要满足连续段的 \(x\) 的条件,而 \(l-1\) 位置满足 \(x\oplus 1\) 的条件。从后往前扫,记录最前的能转移的 0/1 位置,如果发现当前位置满足条件就更新并重置限制。
P2508 只需 \((x+yi)(x-yi)=r^2\),即两个相伴高斯整数之积。为求方案数,将 \(r^2\) 在高斯整数域下唯一分解为高斯素数 \(P\) 内元素。有定理(其中 \(p\) 是奇素数):
然后可以计数。
P4191 模 \(n\) 循环卷积,其中 \(n\) 的质因数很小。
当然可以任意模数 chirp-Z 变换,,,但是一般做法是按某个因数分治 FFT 而不是二叉分治。
CF1349F1
略有理解!出现的数显然是值域前缀;现设 \(a_i\) 为 \(i\) 的第一次出现位置,\(b_i\) 为末次出现位置。则限制:\(a_i\le b_i,a_i\le b_{i+1}\)。画画图,每次让 \(a_i\) 跳到 \(b_{i+1}\) 连个正线,\(b_{i+1}\) 画个反线回到 \(a_{i+1}\)。这样还是不太好用图统计序列;再想想,为啥不把中间出现的位置都用反边跳?这样显然是一一对应,而把访问顺序记下来就是排列。这样构造了对排列的双射。
先考虑统计答案。对排列考虑:每一次出现上升就代表值域 \(+1\),因此每个位置代表的值就是前面的上升个数。因此可以通过欧拉数统计答案。
P2048 把二分统计答案的部分拉来可持久化即可。
P7518 直接每个点找序列的下一个出现位置即可?
P7712 这是割点,只是连边很奇怪。跑 tarjan 过程,运用可持久化线段树求出一个点连到的边。
AGC048F AGC 笑传之充充要:hanghang 可以场切。贪心每次找出最长好子序列记为 \(l_{1:k}\),则你的数需要满足:
证明好像不难??然后直接 dp 即可。
CF1621H 看上去好像不难,但是题面实在是太长了。
CF1349F2 似乎从双射出发不如直接 GF?欧拉数是一个非常奇怪的东西,题解的思路是逆用二项式反演(??)得到式子:
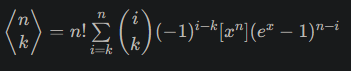
最后需要计算
这里加入 \(y\) 来区分信息。
这里只需要求出 \([x^{n+1}]\),只需求一项考虑拉饭的形式。设 \(F=H\circ W,G=\frac{1}{(1-xy)(1-H)}\),其中 \(W=xF\)。然后只需计算 \([x^{n+1}]G(W(x))\)。
P6071 相当于走到虚树。如果 \([l,r]\) 全在或部分在子树内,则容易。否则分讨路径是否拐弯。拐弯则一定是到根,否则是到虚树抚琴的距离,对 dfs 序前后考虑即可。
CF1184A3 相减得到 \(p\mid F_r(\Delta w)\),而我们知道多项式具有良好的随机性,因此可以近似为随机分布,找到的概率是 \(\sim \frac 1e\)。要求出 \(O(1)\) 次 \(F_r(\Delta w),r\in[0,p-1]\) 即可,这个可以找到原根然后 chirp-Z 变换。
2024.4
CF1764G 神秘构造题。\(/2\) 的操作可以处理配对 \((2x,2x+1)\),如果是奇数可以直接通过配对信息判断。偶数需要去除 \(n\) 的影响,这个找到即可,需要 \(30\) 次。注意第一次需要 \(n\) 后 \(n\) 在 \(mid\) 那侧是不会改变的,所以其实只需要 \(21\) 次。G3 是对最后的过程进行神秘优化,不太懂。
CF1896G 又是神秘卡常(操作次数常)构造。一个一个找,每次最大值没了就随便拉个小丑充数,每次需要 \(2\) 次操作来得到新信息。多 \(n\) 次。注意到(?)最后 \(n\) 次询问开始时,有 \(n-1\) 个人是到处流窜的,这些人是可以找到的并且不会成为答案,然后拿他们充数即可。
P4003 zhicheng 最爱题。首先黑白染色,S 向白点,黑点向 T,每个点在四个边处建点,白点连向隔壁黑点,然后旋转用费用流刻画。
ARC128F 首先是充要条件的选取:选择序列 \(\max(A-B)\ge 1\) 是不利于计算的,更好的是 \(a_i\ge 2i-1\)。这点就可以用折线模拟插入优先队列的过程,然后进行折线容斥。
ARC154F 榉木函数题。定义随机变量的榉木函数为
有:\(M_{X+Y}=M_XM_Y,M_X=P_X\circ \exp\),其中 \(P_X\) 是概率生成函数。直接做即可。
CF1896F2 首先 \([a\neq b]=a+b-2ab\),这样可以得到
因此所有循环移位都必须距离为 \(N/2\),也只需满足所有循环移位距离相等。用循环卷积刻画:
转写为 DFT 形式,设 \(A,B\) DFT 之后是 \(p,q\) 则 \(\forall i\ge 1,p_iq_i=0\)。
考虑对 \(\langle p_i\rangle\) 做蝴蝶变换(长为 \(N\),就是 FFT 开始那个交换数组),根据 FFT 的过程可以证明:
设 \(t=V_2(n)\),\(\langle c_i\rangle\) 是 \(\langle p_i\rangle\) 的蝴蝶变换:
经典结论:\(\omega_N^0,\omega_N^1,\omega_N^{\frac N2-1}\) 在 \(\Q[\omega_N]\) 上线性无关。因此 \(p_n\) 等于零当且仅当 \(\sum_{l=i2^{t+1}}^{i2^{t+1}+2^t-1}c_l-\sum_{l=i2^{t+1}+2^t}^{i2^{t+1}+2^{t+1}-1}c_l\) 全为 \(0\)。
这又得到(航航 AK 了):以 x 为 lowbit 的 \(p\) 必须相等。对 lowbit 状压(不是很懂这个 dp)。
设 \(dp(i,j,x)\) 为第 \(i\) 层,\(j\) 棵子树,里面有 \(x\) 个 \(1\) 的方案数,向上合并得到 \(O(poly(N))\)。注意到和 FFT 改变 \(\omega\) 的角标类似,\(x\) 在 \(S\) 钦定下面有 \(c\) 个 \(1\) 之后只需要把 \(2^c\) 作为单位:必须整除 \(2^c\)。这时需要把集合扔进去。设 \(dp(i,S,j,x)\) 是第 \(i\) 层,\(j\) 棵子树,\(S\) 是下面所选的集合。设 \(c=|S|\),\(x\) 意思是里面有 \(x\times 2^c\) 个 \(1\) 的方案数,向上合并即可。这个过程是卷积:如果钦定 \(S\) 选,那么必须左右子树大小相等。否则就是普通卷积。得到 \(O(N^2\sqrt N)\)。
CF1168E 调整发,困难。每次随机取未使用 p,看看能不能上一个 q,如果不能就随机搞一个未使用 a 踢掉原来的 q。!!
CF720D 不太懂。
ABC270H PGF 笑传之始终终。算出始态到终态的 XYF \(F\),即 \([x^i]F\) 是 \(i\) 步到达了终态的概率。同样算出终态到终态的 XYF \(G\),则有 PGF \(P=F/G\)。这样算 \(P'(1)\) 即可!
ARC136F 这和开关很像。和上一道题差不多的 trick,只是问题是这里算出来是 EGF,还需一个拉普拉斯变换到 XYF。
AGC058D 自动计算容斥系数 trick!!对 ABCABCA 这样的串容斥,设系数的 OGF 为 \(F\),则 \(SEQ(F)=1+x+x^2\)(应该也有组合的说法,因为结果是简单的)。这样算出来即可直接做。
P3923 有限域构造。构造 \(\mathbb F_p\) 直接是同余,\(\mathbb F_{p^k}\) 就是对 \(Z_p\) 上的 \(k\) 次素多项式取模。这个素多项式应该可以枚举出来。
CF923E 矩阵对角化题目。分解 \(A=P^{-1}BP\) 的方法是找到矩阵的特征值、特征向量 \(\lambda_i,v_i\)。然后把 \(\lambda\) 扔进 \(B\),\(v\) 扔进 \(P\)。由于最近发现多项式求根是可以做的,说不定可以搬联考?但是这道题具有很特殊的形式。
新近知道有 GF 做法,当时我没做出来。
P6776 重新思考。但是想了一半觉得这不是纱布题吗?然后看题解之后发现有小问题。
\(T_1\) 在 \(T_2\) 上的匹配是 \(T_2\) 若干点的和 \(T_1\) 同构的虚树,满足选了左儿子一定选右儿子。因此 联系淑芬 不难想到只需找一颗深度大于给的最大深度的树即为充要。直接对一个集合判定:如果单点直接胜利;分开双子树、左子树、右子树。重点是双子树情况。而深度只需要一边深就可以了,另一边可以直接放最强的情况:一个点。这样直接递归即可。
P8147 似乎直接 AC 自动机建虚树即可。但是 AC 自动机又忘了。
ARC173F 之前写过题解但是有点复杂,降阶公式也没有得到精髓。
P2603 废话很多但是决定点集相似的是比例和夹角。AC 自动机即可。
CF1119H 神迷题。计算(异或卷积)
考虑 \([z^p]\hat F_i\),即每项的第 \(p\) 位 FWT 值。而此为
现在考虑 \(d_j\) 前带的系数出现次数,设为 \(c_k\),其中 \(k\) 的第 \(x\) 位 \(=[p\odot a_{i,j}\bmod 2]\)。神秘地,考虑 \(b_{i,T}=\oplus_{j\in T} a_{i,j}\),设
而
全都拉出来,相当于 \(\hat C\),IFWT 就得到了 \(C\)!!
复杂度很好 \(O(nm2^m+(m+k)2^{m+k})\),其中 \(V=2^k\)。
P7603 减半报警器,报警了就重构报警器。
CF1009G 非常简单的调整法,题解
P7834 重构树的简单应用。
P4768 重构树的简单应用。
CF1916H 神秘的 q-analog 相关。
AT_cf17_final_j MST 照样具有可合并性质!!则点分治即可。
P6299 又是高斯整数题??
CF1948G 枚举最小点覆盖然后 Kruskal。
P1963 最小字典序二分图匹配:从后往前取字典序最小的,然后匈牙利即可。本题也有特殊性质。
P4100 排到矩阵里,设 \(AX=B\),如果 \(X_{i,j}=0\) 那么可以 \(p_i=j\)。然后还是最小字典序二分图匹配。
ARC076F 线段树做霍尔定理。
P5296 注意到
然后直接矩阵树。


