Handbook of Enumerative Combinatorics 阅读

Chapter 1 代数几何方法

Part1 代数方法

1.3 生成函数

符号化方法和拉格朗日反演

拆分数的生成函数和五边形数定理、斐波那契的拆分数

平面二叉树（Plane Binary Tree）、三角剖分、Dyck Path 的等价和双射及 k 叉

金字塔结构（没有认真看）

错排列

\[\sum_{i\ge 0}\frac{D_n}{n!}=e^{-\log(1-x)-x} \]

欧拉数(Euler numbers)

计数 \(n\) 阶排列满足

\[a_1>a_2<a_3>a_4<a_5\dots \]

使用 EGF。

假设这个组合类是 \(\mathcal P\)。把大于小于取反的组合类 \(\mathcal P'\cong \mathcal P\)。

考虑插入最大值：

\[\mathcal P\times \bullet \times \mathcal P+1=Shift(\mathcal P+\mathcal P') \]

那么就得到了 \(P^2+1=2P'\)，并且 \(P(0)=1\)。

解微分方程得到 \(P=\sec x+\tan x\)。据说根据这个可以得到一些三角恒等式的组合意义。

带符号图计数

带符号图是两个点之间有独立的正边和负边（都可以没有）的无向图。任意环都有偶数个负边的带符号图称为平衡的，反之亦然。

首先设任意（无符号）无向图的生成函数是

\[F(x,y)=\sum_{n\ge 0}\frac{x^ny^{\binom n2}}{n!} \]

设 \(S(x,y_+,y_-,z)=\sum_G \frac{x^v}{v!}y^{c_+}_+y^{c_-}_cz^e\)

\(v\) 是点数，\(e\) 是边数，\(c_+,c_-\) 是平衡的连通分量/不平衡的连通分量个数。

设 \(B(x,y_+,z),C_+(x,z),C_-(x,z)\) 是平衡的、连通平衡的、连通不平衡的图的生成函数。

我们有：

\[B=\exp(y_+C_+),S=\exp(y_+C_++y_-C-) \]

那么

\[C_+(x,z)=\frac 12 \ln B(x,2,z),C_+(x,z)+C_-(x,z)=\ln S(x,1,1,z) \]

转而计算 RHS。

首先

\[S(x,1,1,z)=\sum_{e,v\ge 0}\binom{v(v-1)}{e}\frac{x^v}{v!}z^e=F(x,(1+z)^2) \]

考虑怎么计算 \(B(x,2,z)\)。首先注意到肯定是不能有正负边同时存在的。然后平衡图和每个点有符号，边符号是两点符号乘积的标记图（Marked Graph）是双射的。

这样就有：

\[B(x,2,z)=\sum_{e,v\ge 0}\binom{\binom v2}{e}2^v\frac{x^v}{v!}z^e=F(2x,1+z) \]

那么：

\[S(x,y_+,y_-,z)=F(2x,1+z)^{(y_+-y_-)/2}F(x,(1+z)^2)^{y_-} \]

有理

什么样的生成函数是有理（Rational）的？

如果 \(A(x)=\sum a_nx^n\) 是一个系数满足线性递推(c-recursive)的 OGF，即

\[\sum_{i=0}^d a_{n-i}c_i=0 \]

设 \(q(z)=(1-r_1z)^{d_1}\cdots (1-r_kz)^{d^k}\)，那么 \(A\) 就应该是有理的，具体来说：

\[\exists \deg p(x)<d,A(x)=\frac{p(x)}{q(x)} \]

此外，我们知道斐波那契数有所谓封闭形式；事实上所有有理 OGF 的系数都有封闭形式，即：

\[\exists f_{1:k}(x),\deg f_i(x)<d_i,a_n=\sum_{i=1}^k f_i(n)r_i^n \]

这些命题是等价的。

微分有限和代数

微分有限（D-finite），即存在一个多项式为系数的微分方程；具体地，存在系数 \(q_{0:d}(x)\) 使得：

\[\sum_{i=0}^d q_i(x)A^{(d-i)}(x)=q(x) \]

类似我们说的代数数，一个生成函数是代数（Algebratic）的，当存在系数 \(q_{0:d}(x),q(x)\) 使得：

\[\sum_{i=0}^d q_i(x)A^{d-i}(x)=0 \]

一个生成函数是整式递推（P-recursive）的，当且仅当存在一组多项式来把线性递推的常数换成多项式。

这些东西有如下的关系：

比较神秘的就是代数 \(\Rightarrow\) 微分有限和整式递推 \(\Rightarrow\) 微分有限。

均可在线性空间上考虑。

代数意味着 \(C(x)\) 域扩张 \(A\) 后的 \(C(x,A)\) 是在 \(C(x)\) 上至多 \(d\) 维（设代数的那个式子有 \(d\) 项）的线性空间。那么考虑 \(A(x)\) 的各阶导数 \(A,A',A''\dots A^{(d)}\) 应该是在 \(C(x)\) 上线性有关的。

整式递推的 \(c_i(x)\) 如果希望转成微分方程的系数，则只需注意到 \(\{(x+i)^{\underline k},k\in \mathbb N\}\) 是 \(C(x)\) 的一组基。也就是说一般幂转为下降幂，然后扔进对应位置的微分方程即可。

我知道了若干基本函数的各项性质，那么我怎么去推其他的函数呢？

方法就是通过各项运算得到。下面的表列出了各项运算是否维持性质，星星是对位相乘。

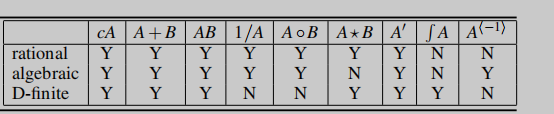
进一步地，\(A(x)\) 在逆下维持微分有限当且仅当 \(A'(x)/A(x)\) 是代数的；微分有限函数复合代数函数是微分有限的。

证明可以考虑线性空间来维护（这也是代码实现的基础）。但是具体来说这个可能只作为判定标准，因为实现太繁重了，只能手动找。

https://www.cnblogs.com/joke3579/p/-/ode-automaton 这里有一个小小实现。

此外，高维的多项式的对角线（即各变量次数一样）是微分有限的。

1.4 线性代数方法

首先对图有几个矩阵：

• 有向图、无向图的邻接矩阵 \(A\)

• 有向图的频率矩阵（incidence matrix）\(M\) 是 \(V\times E\) 的：

  \[m_{v,e}=\left\{\begin{matrix} -1 & e=(v,x)\\ 1 & e=(x,v)\\ 0 & \text{otherwise} \end{matrix}\right. \]

• 拉普拉斯矩阵 \(L\) 是 \(V\times V\) 的：当 \(u=v\) 时 \(L_{u,v}=\deg u\)，否则是 \(-A_{u,v}\)。在有向图上是出度。

• 对无向图而言，如果 \(M\) 是任一定向的频率矩阵，那么 \(L=MM^T\)。

路径计数

\(u,v\) 之间的 \(n\) 步路径计数。根据经典结论，这就是 \(A^n_{u,v}\)。

推论：下式是有理函数。

\[\sum_{n\ge 0}A^n_{u,v}x^n \]

证明：

\[\sum_{n\ge 0}A^n_{u,v}x^n=((I-xA)^{-1})_{u,v}=(-1)^{u+v}\frac{\det(I-xA:v,u)}{\det (I-xA)} \]

这是由于克拉默法则（不是那个求线性方程组解的阉割版。。）。

对于无向图，邻接矩阵是对称的，因而是可对角化的。因此，特殊地，有

\[\text{number of walks of length n from u to v}=\sum_{i=1}^n c_i\lambda _i^n \]

其中 \(\lambda _i\) 是 \(A\) 的特征值。

矩阵树定理

先是无向图。记值为 \(c(G)\)。

一个简明的证法（我又学了阉割版的柯西比内公式。。）。

由于

\[\det L_v=\sum_{S\subset [E],|S|=V-1}\det M_v[S]\det M_v^T[S]=\sum_{S\subset [E],|S|=V-1}\det M_v[S]^2 \]

而 \(\det M_v[S]\) 仅当 \(S\) 是生成树的时候才是 \(\pm 1\) 否则是 \(0\)。

因为如果出现环就代表向量线性相关，\(\det\) 就是 \(0\)；没出现环就是生成树，这时候按照某个剥叶子的顺序重排频率矩阵就得到了一个只有对角线上有 \(1/-1\) 的值的矩阵，行列式是 \(1/-1\)。

证毕。

上面也表明

\[c(G)=\frac 1n \prod_{i=1}^{n-1}\lambda _i \]

其中 \(\lambda _{1:n-1},\lambda _n=0\) 是 \(L(G)\) 的特征值。

对于有向图，统计的是内向树。但是特征值的等式当图是平衡的（即 \(\forall u,outdeg_u=indeg_u\)）才成立。

BEST 定理

• 一个图存在欧拉回路当且仅当图平衡。

欧拉回路的个数是：

\[c(G,v)\times \prod _{u}(outdeg_u-1)!,\text{for any }v \]

证明可以参见 BEST 定理题解区。

Pfaffian 和完美匹配

记完美匹配数是 \(m(G)\)。

斜对称矩阵 \(A\) 是满足 \(A^T=-A\) 的矩阵。这个 \(2n\times 2n\) 矩阵 \(A\) 的 Pfaffian 记为 \(Pf(A)\)。

要得到 \(Pf(A)\)，枚举每个完美匹配 \(M=\{(a_i,b_i)\}(a_i<b_i)\)，则设 \(sign(M)\) 是 \((-1)^d\)，其中 \(d\) 是在线上按序标出 \(1\dots 2n\) 后，用完美匹配连接半圆后的交点个数。\(a_M\) 则是 \(\prod A_{a_i,b_i}\)。则

\[Pf(A)=\sum_M sign(M)a_M \]

定理：

\[\det (A)=Pf(A)^2 \]

对于斜对称矩阵 \(A\)。\(Pf(A)\) 取正值。

给了一个 Sketch of Proof 但是我没看懂（24 年的集训队轮文上也只是扔了个结论。。）

但是模意义下不能（据小芬图等人）区分二次剩余的正值、负值，所以在模意义下采取消元的方法。

对于一个无自环的无向图，设某个定向之后的带符号邻接矩阵 \(S\) 是反边标记为 \(-1\) 的邻接矩阵。这样的 \(S\) 是反对称的。

如果我可以使得每个完美匹配的 sign 在 \(S\) 上都一样那就赢了。但是输了是因为不一定所有图都可以容易地找到或者干脆没有。事实上，任意图的完美匹配计数是 P-Hard 的；但是对于平面图不仅存在而且我们可以在 \(O(n^3)\) 时间内做到（不多于消元复杂度），参见 FKT 算法。

对于 \(1\times 2\) 的骨牌覆盖矩形问题，我们可以利用这个得到通项公式，参见 闲话。

LGV 引理

一个小应用是 闲话，还有一个汉克尔矩阵（Hankel matrices）好像跟连分数有关但是我不会连分数阿。

计算行列式

• 各类奇技淫巧

偏序集

一个偏序集 \((P,\le)\) 是一个集合配备了二元关系 \(\le\)。必须满足：

• \(p\le p\)
• \(p\le q,q\le p\Rightarrow p=q\)
• \(p\le q,q\le r\Rightarrow p\le r\)

称 \(p<q\)，如果 \(p\neq q,p\le q\)；称元素 \(p,q\) （不）科比，当 \(p<q\) 或 \(p>q\)。称 \(p\) 包含 \(q\)，当 \(\nexists r\in P,q>r>p\)，记为 \(p\succ q\)。

有几个下面我们会提及的偏序集：

• \([n]\)：\(1,2,3\dots n\)，自然数。
• 子集晶格 \(2^A\)：一个集合的所有子集，关系是包含。
• 整除晶格 \(D_n\)：一个数的所有因数，关系是整除。
• 布吕阿序（Bruhat order on permutations）：\(S_n\)，关系是 \(A\succ B\)，当 \(B\) 可以通过一次邻项逆序对交换得到 \(A\)。
• 有限域晶格：\(L(\mathbb F_q^n)\)，是 \(\mathbb F_q^n\) 在 \(\mathbb F_q\) 上线性空间的所有子线性空间，关系是包含。

一个偏序集的哈斯图是把包含关系连边的图。

一个偏序集的区间 \([p,q]=\{r\mid p\le r\le q\}\)。一个偏序集是局部有限的，当所有区间都是有限的。

两个偏序集 \(P,Q\) 的直和 \(P+Q\) 是 \(P\cup Q\)，\(P,Q\) 之间没有大小关系；直积 \(P\times Q\) 是 \((p,q)\) 的集合，两个元素 \((p,q)\) 和 \((p',q')\) 当 \(p\le p',q\le q'\) 时才科比。

一个偏序集的子集是链，当所有元素之间都科比；反链是都不科比。链长度是大小 \(-1\)。

如果存在一个函数 \(r:P\to \mathbb N\)，满足所有最小元（没有更小的元素）\(x\) 满足 \(r(x)=0\)，而 \(\forall p\succ q,r(p)=r(q)+1\)，，则称 \(P\) 是可秩的（Ranked）。\(P\) 的秩是最大的 \(r\)。有限可秩偏序集的秩生成函数是

\[R(P;x)=\sum_{p\in P}x^{r(P)} \]

晶格（Lattice）

满足任意两个元素 \(p,q\) 都存在最小的公共上界和最大的公共下界的偏序集是晶格。这分别称为 join 和 meet。（我也不知道怎么翻译好。。）

上面所列举除了布吕阿序全都是晶格。

一个晶格必定有唯一最小元、最大元 \(\hat 0,\hat 1\)。满足 \(x\succ \hat 0\) 的 \(x\) 叫做原子（atom）。

容易发现：为了证明一个偏序集是晶格，只需说明存在 \(\hat 1\) 和 \(\lor\) 即可。

分配晶格（Distributive Lattice

分配晶格是满足 \(\land,\lor\) 互相具有分配律的晶格（参考 \(\cap,\cup\)）。

一个偏序集的序理想（Ordered Ideal） \(I\) 是一个集合满足 \(i\in I,j<i\Rightarrow j\in I\) 的子集（莫名想到戴德金分割？）。\(J(P)\) 是所有序理想的偏序集，关系是包含。

有限分配晶格基本定理：

偏序集 \(L\) 是分配晶格，当且仅当 \(\exists\) 偏序集 \(P\)，\(L\cong J(P)\)。

证明：

首先说 \(J(P)\) 是分配晶格。这是因为 \(J(P)\) 是 \(2^A\) 子集晶格的子集，是满足分配性的。

然后取 \(L\) 中不可约的元素 \(x\)，即 \(x>\hat 0\) 且 \(\nexists a,b<x,a\lor b=x\)。在分配晶格中，这就是说 \(x\le a\lor b\Rightarrow x\le a\) 或 \(x\le b\)。

这样的 \(x\) 的集合 \(P\) 维持偏序关系。我们证明 \(L\cong J(P)\)。

构造映射

\[\varphi :L\to J(P)\\ \varphi (x)=\{a\mid a\le x,a\in P\},\varphi^{-1}(A)=\lor _{a\in A}a \]

这个映射是双射。由于：

设 \(S\subset P\)，\(x=\lor S\)，\(T=\{a\mid a\in P,a\le x\}\)，有 \(S=T\)（因为 \(S\subset T\)，\(T\) 又由于不可约 \(\subset S\)）。

设 \(x\in L\)，\(S=\{a\mid a\in P,a\le x\}\)，\(y=\lor S\)，则 \(x=y\)。首先 \(y\le x\)，但是由不可约有 \(x\le y\)。

根据 Dilworth 引理（熟知），最长反链等于最小链划分。记此值为 \(w\)，是偏序集 \(P\) 的宽度（width）。

那么：任意分配晶格 \(L\cong J(P)\) 一定可以作为子偏序集映入 \(\N^w\)。

构造：

\[\varphi : J(P)\to \N^w\\ \varphi(I)=(|I\cap C_1|,|I\cap C_2|,\dots |I\cap C_w|) \]

其中 \(C_{1:w}\) 是最小链划分。

Zeta 多项式相关

记重链（multichain）是可以出现（\(c_i\le c_j\)）的链（科比不能相等！）。

设 \(Z_P(k)\) 是偏序集 \(P\) 中 \(k-2\) 长度的重链的计数。那么：这是一个多项式，称为 Zeta 多项式，由

\[Z_P(k)=\sum_{i\ge 2}b_i\binom{k-2}{i-2} \]

给出，其中 \(b_i\) 是 \(i-2\) 长度链计数。例如，\([n]\) 的 zeta 多项式就是

\[Z_{[n]}(k)=\binom{n+k-2}{n-1} \]

设序多项式 \(\Omega_P(k)\) 是 \(f:P\to [k]\) 的函数计数，满足 \(p<q\Rightarrow f(p)\le f(q)\)。

则有：\(\Omega_P(k)=Z_{J(P)}(k)\)。

证明：这是说，序理想满足：

\[f^{-1}(\{1\})\subset f^{-1}(\{1,2\})\subset \dots \subset f^{-1}([k]) \]

这是 \(J(P)\) 上的重链。显然，这是双射。

一个偏序集的线性扩展 \(e(P)\) 是哈斯图上的拓扑序计数。

考虑 \(e':J(P)\to \N\)

\[e'(I)=[I=\hat 0]+\sum_{J\prec I} e'(J) \]

这样得到的 \(e'(\hat 1)\) 就是答案。树的拓扑序计数和勾（钩）子（长）公式就是根据这个而来。

偏序集莫比乌斯反演

设 \(Int(P)\) 是所有区间的集合。

莫比乌斯函数 \(\mu :Int(P)\to \Z\)，递归定义：

\[\sum_{r\in [p,q]}\mu (p,r)=[p=q] \]

一元莫比乌斯函数则是 \(\mu(x)=\mu(\hat 0,x)\)。设 \(\mu(P)=\mu(\hat 0,\hat 1)\)。

我们举出上面提到的例子的莫比乌斯函数。

\[\mu_{[n]}(i,j)=[i=j]-[j=i+1]\\ \mu_{2^A}(S,T)=(-1)^{|S|-|T|}\\ \mu_{D_n}(k,l)=\mu(l/k),\text{second }\mu\text{ is the one in Number Theory}\\ \mu_{S_n}=(-1)^{\tau(A)-\tau(B)}\\ \mu_{L(\mathbb F_q^n)}(U,V)=(-1)^dq^{\binom d2},\text{where }d=\dim V/U\\ \mu_{J(P)}(I,J)=(-1)^{|J-I|}[J-I \text{ is an antichain}] \]

第四个的证明是不太容易的，第五个的则在这里。

根据定义，有：

\[g(p)=\sum_{q\ge p}f(q)\iff f(p)=\sum_{q\ge p}\mu(p,q)g(q)\\ g(p)=\sum_{q\le p}f(q)\iff f(p)=\sum_{q\le p}\mu(q,p)g(q)\\ \]

Indeed, one may think of the Mobius function as a poset-theoretic analog of the Fundamental Theorem of Calculus: \(g\) is analogous to the integral of \(f\) , as it stores the cumulative value of this function.

书上给出的评论。

关联代数和计算莫比乌斯函数

一个局部有限偏序集 \(P\) 的关联代数是 \(f:Int(P)\to K\) 的 K-algebra（即 \(K\) 上的线性空间配备了一个双线性乘积）。这里的双线性乘积是狄利克雷卷积，即，

\[f\cdot g=\sum_{q\in [p,r]}f(p,q)g(q,r) \]

这个卷积显然是结合的（但是不交换）。记为 \(I(P)\)。

点乘的单位元是 \({\bf 1}(p,q)=[p=q]\)。

还有一个重要的函数 \(\zeta(p,q)=[p\le q]\)。这个 \(\zeta\) 和我们前面的 zeta function 是有关系的：\(Z_P(k)=\zeta_P^k(\hat0,\hat 1)\)。

类似数论里面我们干的事情，可以得到：\(\mu =\zeta^{-1}\)。

如何计算莫比乌斯函数？我们有几种想法：

• 依据分解计算
• 依据莫反计算
• 依据闭包计算
• 依据重链计算
• 根据拓扑结构计算

分解计算：容易证明：

\[\mu_{P\times Q}((p,q),(p',q'))=\mu_P(p,q)\mu_Q(p',q') \]

这也说明：\(I(P\times Q)\cong I(P)\otimes _K I(Q)\)。

一个例子是计算子集反演的 \(\mu_{2^A}\) 或者数论的 \(\mu_{D_n}\)。

此外，记集合划分为子集的偏序集是 \(\Pi _n\)（关系是否是细化划分）。如果希望计算 \(\mu(p,q)\)，设 \(p\) 对 \(q\) 把每个集合细分为 \(\{a_{1:m}\}\)，则

\[[p,q]\cong \prod_i\Pi_{a_i} \]

只需知道 \(\mu(\Pi_n)\)。同样得到 \(\mu(\Pi_n)=(-1)^{n-1}(n-1)!\)。

莫反计算：

还是计算 \(\Pi_n\)。考虑有 \(q\) 个盒子，把元素放进去，来进行集合划分；空的允许。

那么，钦定集合划分为 \(\pi\)（即可以是更细分），\(\pi\) 是有 \(b\) 块的划分，那么方案数为 \(f(\pi)=q^b\)。一定是 \(\pi\) 的话，方案数是 \(g(\pi)=q^{\underline b}\)。

根据莫反：

\[g(\pi)=\sum_{\rho\ge \pi}f(\rho)\Rightarrow f(\pi)=\sum_{\rho\ge \pi}\mu(\pi,\rho)g(\rho)\\ q^{\underline b}=\sum_{\rho \in \Pi_n}\mu(\hat 0,\rho)q^{|\rho|} \]

比较 \([q^1]\) 得到答案。值得一提的是，这里的拓展是斯特林反演。

闭包（Closure）计算：

定义一个函数 \(\overline \cdot :P\to P\) 是闭包函数(（Closure Operator），当：

• \(p\le \overline p\)
• \(p\le q\Rightarrow \overline p\le \overline q\)
• \(\overline{\overline p}=\overline p\)

设 \(Cl(P)\) 是封闭元素（\(p=\overline p\)）的子偏序集。

则对于 \(p\le q\)：

\[\sum_{\overline r=q}\mu(p,r)=[\overline p=p][\overline q=q]\mu _{Cl(P)}(p,q) \]

设 \(\overline f(p,q)=f(p,q)[\overline p=p][\overline q=q]\)，同样的 \(\overline 1,\overline \zeta,\overline \mu\)；设 \(c(p,q)=[q=\overline p]\)。

则应该有 \(c\overline\zeta=\zeta \overline 1\)。因此：

\[\mu c\overline1 =\mu c\overline \zeta \overline\mu=\mu\zeta \overline 1\overline \mu=1\overline\mu =\overline\mu \]

证毕。

就得到了魏斯纳定理（Weisner Theorem）：对于 \(p<a\le q\)：

\[\sum_{r\in [p,q],r\lor a=q}\mu(p,r)=0 \]

这是因为 \(\overline r= r\lor a\) 是闭包运算。

这个定理可以用来计算第五项，也可以用来计算 p-群偏序集（关系是包含）的莫比乌斯函数。但是我不会群论🤡。

横截定理（Crosscut Theorem）：

设 \(L\) 是晶格，\(X\) 是原子集合，设 \(N_k\) 是 \(k\) 元 \(X\) 的子集满足其 \(\lor\) 是 \(\hat 1\)。z

则：

\[\mu(\hat 0,\hat 1)=\sum_k(-1)^kN_k \]

证明从略。

推论：\(\lor X\neq \hat 1\Rightarrow \mu(\hat 0,\hat 1)=0\)。

这里的应用是分配晶格的 \(\mu\)。若 \(J-I\) 是反链，\([I,J]\cong 2^{J-I}\)；否则，\([I,J]\) 的原子集合是 \(I\cup \min(J-I)\neq J\)，故为 \(0\)。

重链计算：

\[Z_P(-1)=\mu_P(\hat 0,\hat 1) \]

这是因为 \(Z_P(k)=\zeta_P^k (\hat 0,\hat 1)\)，而 \(\zeta^{-1}=\mu\)。

例子是考虑 \(NC_n\)，即不存在 \(a<b<c<d\) 而 \(bel_a=bel_c\neq bel_b=bel_d\) 的划分，是 \(\Pi_n\) 的子集。

据信：

\[Z_{NC_n}(k)=\frac 1n\binom{kn}{n-1} \]

那么就得到了

\[\mu(NC_n)=(-1)^{n-1}C_{n-1} \]

后面几种方法有点神秘了。

欧拉偏序集（Euler Posets）相关

原谅我不会拓扑

Part 2 离散几何方法

我决定先启动 Chapter 2 分析方法。

也就是说这一部分还要很一会才会有内容

鉴定为能看，和分析方法同步更新！

还是把看到的写一写，但是可能接下来没事才看这个了。。。

基本定义和构造

多胞形

设 \(S\subset \R^d=\{v_1,v_2,\dots,v_n\}\)。

\[conv(S)=\{\sum_{i=1}^n\lambda_iv_i\mid \lambda_i\ge 0,\sum_i \lambda_i=1\} \]

也是所有包含 \(S\) 的凸包（定义：任意两点之间的线段被全含）的交集。

一个超平面（hyperplane）是 \(d-1\) 维的仿射子空间（affine subspace），被一个线性关系给出。

\[{\bf a}\in \R^d-{\bf 0},b\in \R,H=\{{\bf x}\in \R^d\mid {\bf a}\cdot{\bf x}=b\} \]

Chapter 2 分析方法