闲话 719 - “猴子程反演”

定义局部有限序集 \(P\) 上的莫比乌斯函数 \(\mu(L,R)\) 是满足如下性质的函数：

\[\mu(L,L)=1,\sum_{L\le x\le R}\mu(L,x)=0 \]

有偏序集 \(L(\mathbb F _n^q)\) 是 \(\mathbb F_n^q\) 的子线性空间，偏序关系是包含。设 \(|\dim U-\dim V|=d\)，证明： \(\mu(U,V)=(-1)^dq^{\binom d2}\)。

一眼就像 q-模拟。。记 \(\mathbb{F}_q^n\)（在模 \(q\) 意义下的 \(n\) 维整数空间）大小为 \(k\) 的线性无关向量组个数有 \(((n)_k)_q\)。

\[((n)_k)_q=q^{\binom k 2}\prod_{i=n-k+1}^n (q^i-1)=\frac{(q-1)^kq^{\binom k 2}[n]_q!}{[n-k]_q!} \]

所以

\[\binom nk_q=\frac{((n)_k)_q}{((k)_k)_q} \]

设 \(\dim V/U=m\)，枚举子空间维数 \(t\)：

\[\sum _{t}\frac{((m)_t)_q}{((t)_t)_q}(-1)^tq^{\binom t2}=\sum _t\binom mt_q(-1)^tq^{\binom t2}=(1+-1)^{(m;q)}=0 \]

证毕。

但是还有更优雅的证明方法。

魏斯纳定理（Weisner's theorem）：对于晶格（lattice）\(L\)，\(p<a\le q\)，有：

\[\sum_{p\le r\le q,r\lor a=q}\mu (p,r)=0 \]

还是记 \(\dim V/U=m\)。首先 \(L(\mathbb F^m_q)\) 是晶格，取 \(a\in \mathbb F_q^m\neq \bf 0\)，\(p=\hat 0,q=\hat 1\)。

那么那些生效的 \([\hat 0,r]\cong L(\mathbb F_q^{m-1})\)，并且不包含 \(a\)。这样的 \(r\) 有 \(q^{n-1}\) 个。那么：

\[\mu (L(\mathbb F_q^m))+q^{m-1}\mu(L(\mathbb F_q^{m-1}))=0 \]

解递归式即可。

按照“莫比乌斯反演”“子集反演的名字，给这个式子取一个名字：“有限域上线性空间反演”。

但是比较尬的事是没有构造出来“容易统计 \(\mathbb F_q^n\) 的所有子空间的信息和，但是不太容易统计 \(\mathbb F_q^n\) 自己的”。

最后的结论：

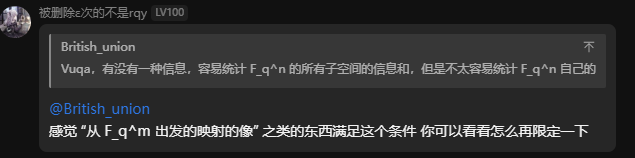
但是不知道怎么做

因为内容比较少所以写点别的。

批话哥：Eltaos_xingyu,nityacke,hanghang

怪话哥：柠檬熟了,Eltaos_xingyu,nityacke,UOB

怪话常用主语：zhicheng,🐒，🐧，🏄‍，hanghang,Eltaos_xingyu 的家人（自用）

尼特打 CF 上分然后获得 NEAR，成为有信用人士。但是提取不出来，信用实则没有。