闲话 711-拉格朗日反演的组合证明

来自于《Handbook of Enumerative Combinatorics》。

准备工作

在开始之前，让我们先回顾无标号的复合（Composition）构造：

设组合类 \(\mathscr C=\mathscr A\circ \mathscr B\)，意思是 \(\mathscr C\) 由这样构造：

对于任意一个 \(x\in SEQ(\mathscr B)\)，设其（序列）长度为 \(k\)，则为这个序列配备一个 \(\mathscr A\) 中 \(k\) 大小的元素，这样的“配备了一个 \(\mathscr A\) 元素的 \(\mathscr B\) 序列”作为 \(\mathscr C\) 的元素，大小为 \(k\)。

容易验证，这就是对应的生成函数复合。

我们还需要知道所谓拉格朗日反演的“组合形式”（Combinatorial version）：

设 \(|\mathscr A_0|=0,|\mathscr A_1|=1\)，和一个形式幂级数 \(A\)：

\[A(x)=x-a_2x^2-a_3x^3\dots \]

我们把这样的“带符号”的 \(A\) 对应的组合类记为 \(\mathscr A'\)。

定义一个组合结构 \(\mathscr A\) 树，是一个有根树，每个非叶子节点有至少两个儿子（儿子有序），并且每个非叶子节点配备（given）了一个大小为儿子个数的 \(\mathscr A\) 结构。\(\mathscr A\) 树的大小定义为叶子的个数。

设 \(C(x)\) 是 \(\mathscr A\) 树组合类的生成函数，应该有（此处及下面写作 \(A^{-1}\) 的都是复合逆）：

\[C(x)=A^{-1}(x) \]

证明：

考察 \(B=A\circ C\) 。这就是 \(\mathscr A'\) 和 \(\mathscr C\) 组合类的复合。有两种情况：只有一颗 \(\mathscr A\) 树，这对应权值为 \(1\)，由于 \(|\mathscr A_1|=1\)。

或者有 \(k\) 颗 \(\mathscr A\) 树，配备了一个大小为 \(k\) 的 \(\mathscr A\) 结构 \(r\)。我们发现，把这个 \(r\) 作为这些 \(\mathscr A\) 树的根，和本来的 \(\mathscr A\) 树结构构成了一一对应的关系。所以，我们可以认为这是一个带权 \(-1\) 的 \(\mathscr A\) 树。

这些都抵消了：除了最简单的 \(\mathscr A\) 树，它只有根节点。所有我们得到了 \(B(x)=x\)。因此就证明了 \(C(x)=A^{-1}(x)\)。

下面还会用到 Raney 引理的一个推论：对于一个和为 \(-1\) 的序列 \(a_{1:n}\)，恰有一个循环置换使得所有真前缀和非负。

此外，下面还会涉及形式洛朗级数，它的运算律和形式幂级数是相似的。

证明

\[n [x^n]A^{-1}(x)=[x^{n-1}]\left(\frac{x}{A(x)}\right)^n \]

我们很熟悉树的结构，但是有必要引入一个新的组合结构：枝（Sprig）。要提及枝，我们先有一颗结构和 \(\mathscr A\) 树类似的树（不过不为其节点配备组合结构）。然后枝是一个从根到叶子的简单路径，满足所有路径上非叶子节点都至少有两个儿子。特殊地，只有根节点的树的唯一枝是根节点。

\(\mathscr A\) 枝也是类似的。和 \(\mathscr A\) 树类似，为其每个非叶子节点配备一个大小等于其儿子个数的 \(\mathscr A\) 结构。而 \(\mathscr A\) 枝 \(v_{1:k}\) 的大小定义为其所有节点的儿子个数和减去 \(k\)。注意到可能会有大小为 \(-1\) 的枝，所以我们使用形式洛朗级数。

考察 \(\mathscr A\) 枝的结构：大体应该是 \(\mathscr A\) 的序列，但是需要排除正下方的节点，所以所有 \(\mathscr A\) 的大小相当于减少了 \(1\)；最后还需要排除根，所以要乘 \(\dfrac 1x\)。

那么我们不难得到 \(\mathscr A\) 枝的生成函数 \(S(x)\)：

\[S(x)=\frac 1x\cdot\frac{1}{1-(a_2x+a_3x^2+\dots)}=\frac{1}{A(x)} \]

那么， \(n\) 个有序的大小和为 \(-1\) 的 \(\mathscr A\) 枝的个数就应该是

\[[x^{-1}]S(x)^n=[x^{-1}]\left(\frac{1}{A(x)}\right)^n=[x^{n-1}]\left(\frac{x}{A(x)}\right)^n \]

到这里我们需要干的事情就是构造一个类似于双射的玩意：构造 \(n\) 个有序的大小和为 \(-1\) 的 \(\mathscr A\) 枝（划分整个 \(\mathscr A\) 枝集合）到一个大小为 \(n\) 的 \(\mathscr A\) 树。

贺张图：

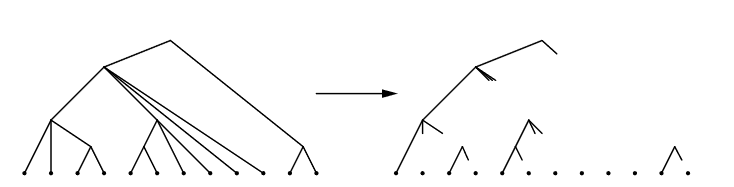
先把树变成 \(n\) 个枝：我们干的事情是把 \(\mathscr A\) 树的叶子（注意儿子是有序的）从左到右，每一个取到其最远祖先的路径作为枝，然后删去这个路径上的所有点。

由于我们的构造（每个非叶子节点至少有两个儿子），这样的过程划分出来的一定是 \(\mathscr A\) 枝。

在这样的构造过程中，我们需要注意一点：按顺序取出的所有 \(\mathscr A\) 枝的大小的真前缀和是非负的，最后和也一定是 \(-1\)。这将在下面说明。

再从 \(\mathscr A\) 枝构造树。我们按顺序放回即可。这样的过程可以进行（而不会放不下）当且仅当真前缀和非负，这是显然的。而根据 Raney 引理， \(n\) 个 \(\mathscr A\) 枝的循环置换恰有一个满足这样的条件。而互为循环置换显然构成对 \(\mathscr A\) 枝集合的划分。

而 \(\mathscr A\) 树的计数已经给出：是 \(A^{-1}\)。这样，我们就组合地证明了拉格朗日反演公式。

真正的闲话：我喜欢 711。