闲话 5.21 四川高联预赛的压轴

求满足下列条件数列个数：

1. 长度为 \(n\)
2. \(\forall i\in[1,n]\quad a_i\not=0\)
3. \(a_1=1\)
4. \(\forall k\in[1,n-1]\quad (a_{k+1}-a_k-1)(a_{k+1}+a_k)=0\)

显然就是不能有 \(0\) 最为重要。义👁坐标系：

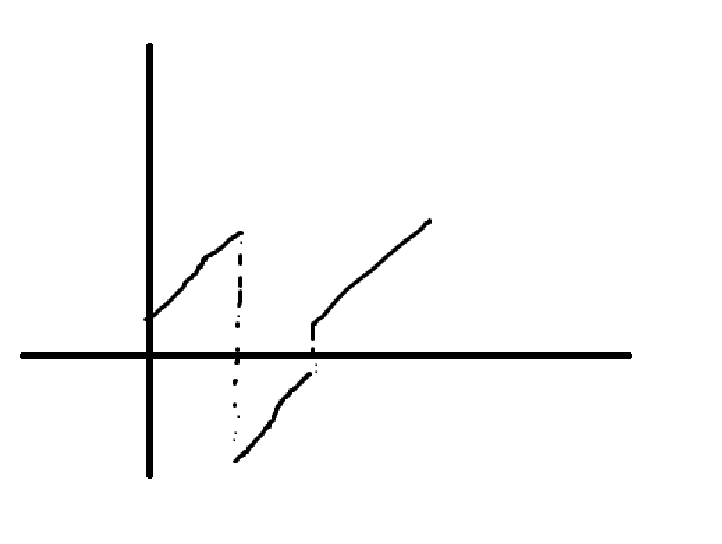
斜上线是 \(a_i=a_{i-1}+1\)，对称是 \(a_i=-a_{i-1}\)。我把在下面的部分对称上来

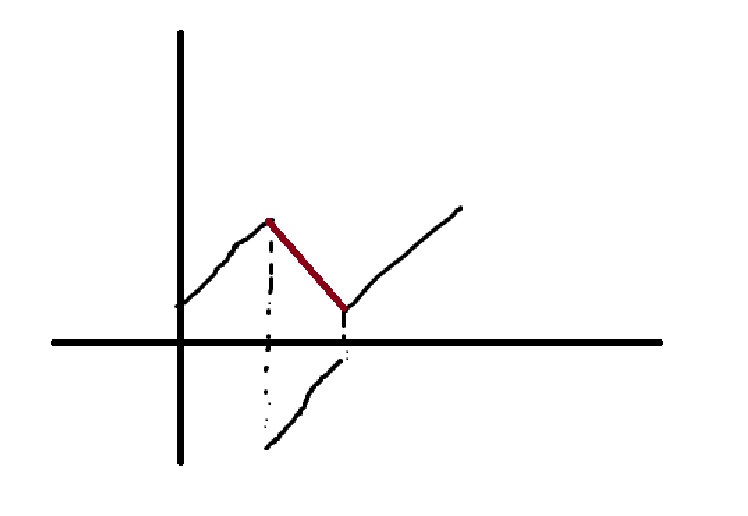
而反射需要步数，不妨认为是平一步。这样，就转化为不能碰到 \(0\)，斜上斜下不能挨一起的 \(n\) 步计数。

然后把斜上变成直右，斜下变成直上，平步变成斜上，不能碰到 \(y=x\)，不能有直角。显然这两个限制互不干涉，这就是说，不能有直角不影响反射容斥。我反射容斥一下就去掉了不能碰到 \(y=x\)。然后统计显然是 trival 的，可以 GF 一下或者其他的。最后答案据信是

\[\binom {n-1}{\lfloor \frac n2\rfloor} \]

倒数第二题是一道复数极值题，不太会阿。倒数第三题据信是椭圆爆算，爆算挺擅长的，就是不太会椭圆。前面题都挺堂的，不知道我去能考多少。