闲话 4.29：伯特兰定理及另一道题

伯特兰公设

任意 \(\ge 4\) 的正整数 \(n\) 满足：存在一个质数 \(p\in (n,2n)\)。

以下 \(p\) 均取质数，\(p_i\) 表示第 \(i\) 个质数。

引理 1：

\[\prod _{p\le n}p\le 4^n,n>1 \]

首先有一个想法：

\[\ln \prod_{p\le n}p\le \pi(n)\ln n\sim n\le n\ln 4 \]

这些放缩是相当松的，因为大约 \(\pi(n)/n\ln n\) 从前几个看起来是在递减而不超过 \(1.2\)（声明：我没学过素数定理）。
所以这容许我们做相当程度的放缩（事实上伯特兰定理也是相当松的）。
从不知道任何素数性质和定理的情况下（在素数的第二节出现）只能考虑归纳。\(2^{2n}=4^n\) 这个形式启发我们从 \(n/2\) 取归纳（但是我之后就没有放缩出来）。

证明：

只需考虑 \(2\nmid n\)。设 \(k=(n\pm 1)/2\) 使得 \(2\nmid k\)。

此时，如果有 \(k<p\le n\)，那么一定有 \(p\nmid k!,p\nmid (n-k)!,p\mid n!\)。那么 \(p\mid \binom nk\)。

所以

\[\prod _{k<p\le n}p\mid \binom nk<2^n \]

这样就证明了命题。

引理 2：

\[\forall p\in (\frac 23 n,n],p\nmid \binom{2n}n,n>3 \]

直接考虑库莫尔定理。设 \(n=k_1p+k_2\)，则 \(k_2+k_2\) 一定不会进位，\(k_1+k_1\) 也不会。

开始证明原命题。

设 \(n\ge 128\)（\(n<128\) 可以被验证），考虑反证。

那么设

\[\binom{2n}n=\prod_{p\le 2n}p^r=\prod_{p\le n}p^r=\prod_{p\le \frac 23n}p^r\\ \le \prod_{p\le \sqrt{2n}}2np\prod_{\sqrt{2n}<p\le \frac 23n}p\\ \le \prod_{p\le \frac 23n}p\prod_{p\le \sqrt{2n}}2n\le (2n)^{\sqrt{n/2}-1}4^{2n/3} \]

而

\[(2n+1)\binom{2n}n\ge 2^{2n} \Rightarrow \binom{2n}n\ge \frac{4^n}{2n} \]

所以得到

\[\frac{4^n}{2n}\le (2n)^{\sqrt{n/2}-1}4^{2n/3}\\ \Rightarrow 4^{n/3}\le (2n)^{\sqrt{n/2}} \]

设

\[f(x)=\frac{x}{3}\ln 4-\sqrt{x/2}\ln 2x \]

大概是这样

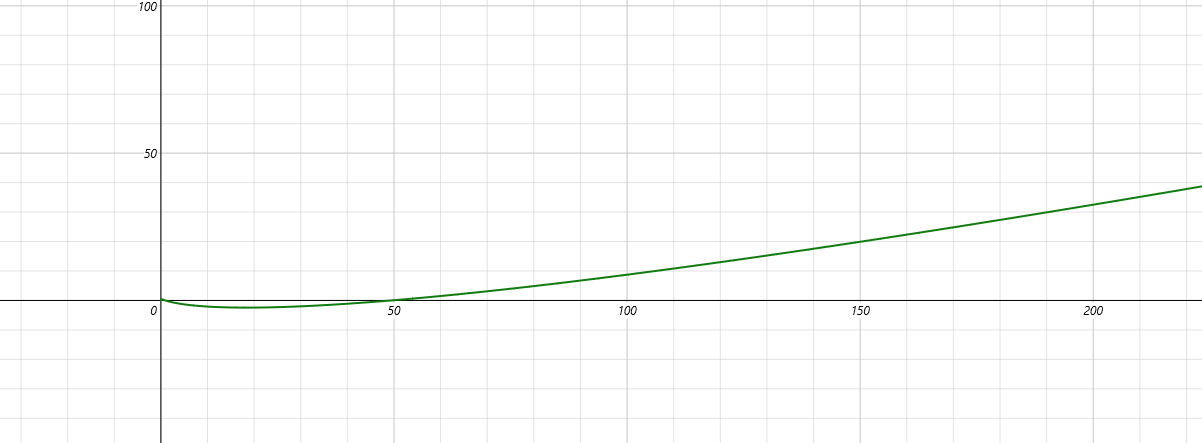
求导可以证明这个在 \(n>128\) 时是正的。矛盾。证毕。

另外题

1.证明 \(n,k\in \N,n>1\)，且 \(a+ik(i=0,1,2,\dots n-1)\) 都是奇素数，那么有：\(p<n\Rightarrow p\mid k\)。

逆元之类的随便反证一下。

2.证明有无穷多个素数非孪生素数的一员。

利用狄利克雷定理考虑 \(30k+23\)。

3.证明非平凡单变元整系数多项式不能只产生素数。

设 \(f(x)=p\)，那么 \(f(kx+p)\equiv 0\pmod p,\forall k\in \Z\)。而 \(f\) 若不为常函数就不能有无限多个点都等于 \(p\)，证毕。